13.2 画轴对称图形课时达标(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
13.2画轴对称图形课时达标
一、选择题
1、下列说法中,正确的是( )
A.作一个图形的对称图形只能作一个
B.作一个图形的对称图形有有限个
C.因为选取对称轴的位置不同,所以作一个图形的对称图形可有无数个
D.不规则的、复杂的图形不存在对称轴
2、与点P(5,-3)关于x
轴对称的点的坐标是(??
)?
??????????
A.(5,3)????????????B.(-5,3)?????
C.(-3,5)???????????
D.(3,-5)
3、作已知点关于某直线的对称第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
4、点(﹣1,﹣5)关于y轴的对称点为(
??)???????????
A.(1,5)???????B.(﹣1,﹣5)?
C.(5,﹣1)??????
D.(﹣1,5)
5、在平面直角坐标中,已知点P(a,5)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(﹣a,5)??????B.(a,﹣5)??????
C.(a-4,5)
D.(﹣a+4,5)
6、在平面直角坐标系中,已知点A(m,3),与点B(4,n)关于y轴对称,那么(m+n)2019的值为( )
A.1??????????B.﹣1?????????C.﹣72019???????
D.72018
7、将△ABC的三个顶点坐标的横坐标都乘以﹣1,纵坐标不变,则所得图形与原图的关系是( )
A.关于x轴对称?????????B.关于y轴对称??
C.关于原点对称?????????D.将图形向下平移一个单位
8、将点A(3,2)向左平移4个单位长度得点A′,则点A′关于y轴对称的点的坐标是( )
A.(﹣3,2)??????
B.(﹣1,2)??????
C.(1,﹣2)??????
D.(1,2)
二、填空题
9、如果点A(a+1,-5)和点B(4,b-2)关于x轴对称,则ab=__________???????????
10、两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在??????????
11、点P(3a+6,3﹣a)关于x轴的对称点在第四象限内,则a的取值范围为_____________.
12、从商场试衣镜中看到某件名牌服装标签上的后5位编码是,则该编码实际上是__________.
13、如图,平面直角坐标系中有四个点,它们的横、纵坐标均为整数.若在此平面直角坐标系内移动点A,使得这四个点构成的四边形是轴对称图形,并且点A的横、纵坐标仍是整数,则移动后点A的坐标为__________.
???
???
???
???
14、如图,在直角坐标平面内,线段AB垂直于y轴,垂足为B,且AB=2,如果将线段AB沿y轴翻折,点A落在点C处,那么点C的横坐标是???????
.
15、如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2019次变换后所得的A点坐标是 ??
.
三、解答题
16、按下列要求画图:画出一个角关于直线l对称的图形;
17、画出△ABC关于直线L的对称图形,标注字母并简要说明.
???
18、点A(-l,4)和点B(-5,1)在平面直角坐标系中的位置如图所示.?????
???
(1)将点A、B分别向右平移5个单位,得到点A1、B1,请画出四边形AA1B1B;
(2)画一条直线,将四边形AA1B1B分成两个全等的图形,并且每个图形都是轴对称图形.
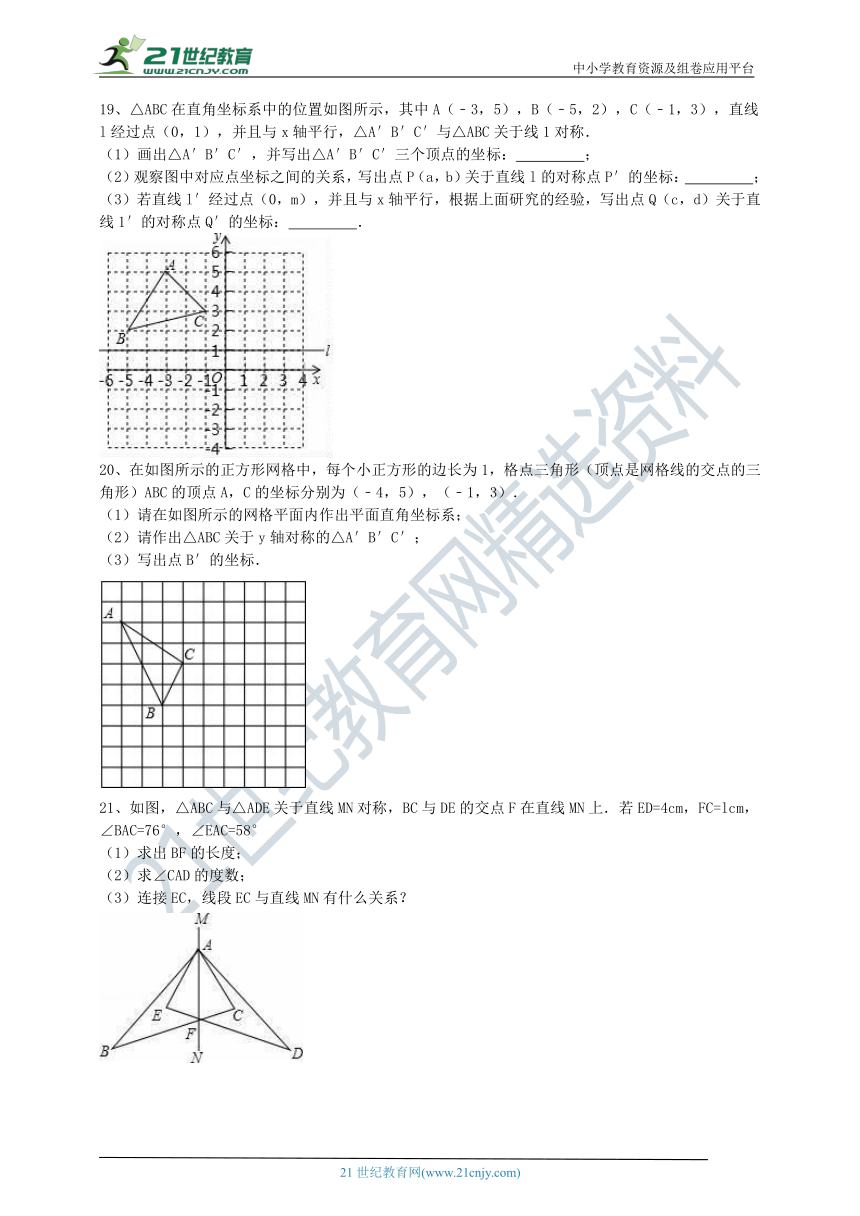
19、△ABC在直角坐标系中的位置如图所示,其中A(﹣3,5),B(﹣5,2),C(﹣1,3),直线l经过点(0,1),并且与x轴平行,△A′B′C′与△ABC关于线1对称.
(1)画出△A′B′C′,并写出△A′B′C′三个顶点的坐标: ??
;
(2)观察图中对应点坐标之间的关系,写出点P(a,b)关于直线l的对称点P′的坐标: ??
;
(3)若直线l′经过点(0,m),并且与x轴平行,根据上面研究的经验,写出点Q(c,d)关于直线1′的对称点Q′的坐标: ??
.
20、在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
21、如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=lcm,∠BAC=76°,∠EAC=58°
(1)求出BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系?
参考答案
一、选择题
1、C
2、A?
3、B
4、D??
5、D.解:∵直线m上各点的横坐标都是2,
∴直线为:x=2,
∵点P(a,5)在第二象限,
∴a到2的距离为:2﹣a,
∴点P关于直线m对称的点的横坐标是:2﹣a+2=4﹣a,
故P点对称的点的坐标是:(﹣a+4,5).
6、B.解:∵点A(m,3)与点B(4,n)关于y轴对称,
∴m=﹣4,n=3,
∴(m+n)2019=(﹣4+3)2019=﹣1,
二、填空题
9、21
10、对称轴上??
11、﹣2<a<3
【解答】解:∵P关于x轴的对称点在第四象限内,
∴点P位于第一象限.
∴3a+6>0①,3﹣a>0②.
解不等式①得:a>﹣2,
解不等式②得:a<3,
所以a的取值范围是:﹣2<a<3.
故答案为:﹣2<a<3.
12、BA629 点拨:假定最左侧或右侧有一条直线为对称轴,沿此直线折叠都会得到BA629,或将此图案从反面观察,也可得到BA629.
13、(-1,1)或(-2,-2)
14、一2
15、(﹣a,b)解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2019÷4=504余3,
∴经过第2019次变换后所得的A点与第三次变换的位置相同,在第二象限,坐标为(﹣a,b).
三、解答题
16、解:如下图
17、解:如图所示,
即为所求.
?
18、解:(1)如图,A、B两点、连线得四边形AA1B1B.
(2)如图,画一条直线A
B1或B
A1即可.
四、解答题
19、【解答】解:(1)如图所示,△A′B′C′即为所求,A'(﹣3,﹣3),B'(﹣5,0),C'(﹣1,﹣1);
故答案为:A'(﹣3,﹣3),B'(﹣5,0),C'(﹣1,﹣1);
(2)由题可得,点P'的横坐标为a,
设点P'的纵坐标为y,则=1,
解得y=2﹣b,
∴点P(a,b)关于直线l的对称点P′的坐标为(a,2﹣b),
故答案为:(a,2﹣b);
(3)由题可得,点Q′的横坐标为c,
设点Q'的纵坐标为y,则=m,
解得y=2m﹣d,
∴点Q(c,d)关于直线1′的对称点Q′的坐标为(c,2m﹣d).
故答案为:(c,2m﹣d).
20、【考点】作图-轴对称变换.
【分析】(1)根据顶点A,C的坐标分别为(﹣4,5),(﹣1,3)建立坐标系即可;
(2)作出各点关于y轴的对称点,再顺次连接即可;
(3)根据点B′在坐标系中的位置写出其坐标即可.
【解答】解:(1)如图所示;
(2)如图所示;
(3)由图可知,B′(2,1).
【点评】本题考查的是作图﹣轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.
21、【解答】解:(1)∵△ABC与△ADE关于直线MN对称,ED=4cm,FC=1cm,
∴BC=ED=4cm,
∴BF=BC﹣FC=3cm.
(2)∵△ABC与△ADE关于直线MN对称,∠BAC=76°,∠EAC=58°,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD﹣∠EAC=76°﹣58°=18°.
(3)结论:直线MN垂直平分线段EC.理由如下:
∵E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
13.2画轴对称图形课时达标
一、选择题
1、下列说法中,正确的是( )
A.作一个图形的对称图形只能作一个
B.作一个图形的对称图形有有限个
C.因为选取对称轴的位置不同,所以作一个图形的对称图形可有无数个
D.不规则的、复杂的图形不存在对称轴
2、与点P(5,-3)关于x
轴对称的点的坐标是(??
)?
??????????
A.(5,3)????????????B.(-5,3)?????
C.(-3,5)???????????
D.(3,-5)
3、作已知点关于某直线的对称第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
4、点(﹣1,﹣5)关于y轴的对称点为(
??)???????????
A.(1,5)???????B.(﹣1,﹣5)?
C.(5,﹣1)??????
D.(﹣1,5)
5、在平面直角坐标中,已知点P(a,5)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(﹣a,5)??????B.(a,﹣5)??????
C.(a-4,5)
D.(﹣a+4,5)
6、在平面直角坐标系中,已知点A(m,3),与点B(4,n)关于y轴对称,那么(m+n)2019的值为( )
A.1??????????B.﹣1?????????C.﹣72019???????
D.72018
7、将△ABC的三个顶点坐标的横坐标都乘以﹣1,纵坐标不变,则所得图形与原图的关系是( )
A.关于x轴对称?????????B.关于y轴对称??
C.关于原点对称?????????D.将图形向下平移一个单位
8、将点A(3,2)向左平移4个单位长度得点A′,则点A′关于y轴对称的点的坐标是( )
A.(﹣3,2)??????
B.(﹣1,2)??????
C.(1,﹣2)??????
D.(1,2)
二、填空题
9、如果点A(a+1,-5)和点B(4,b-2)关于x轴对称,则ab=__________???????????
10、两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在??????????
11、点P(3a+6,3﹣a)关于x轴的对称点在第四象限内,则a的取值范围为_____________.
12、从商场试衣镜中看到某件名牌服装标签上的后5位编码是,则该编码实际上是__________.
13、如图,平面直角坐标系中有四个点,它们的横、纵坐标均为整数.若在此平面直角坐标系内移动点A,使得这四个点构成的四边形是轴对称图形,并且点A的横、纵坐标仍是整数,则移动后点A的坐标为__________.
???
???
???
???
14、如图,在直角坐标平面内,线段AB垂直于y轴,垂足为B,且AB=2,如果将线段AB沿y轴翻折,点A落在点C处,那么点C的横坐标是???????
.
15、如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2019次变换后所得的A点坐标是 ??
.
三、解答题
16、按下列要求画图:画出一个角关于直线l对称的图形;
17、画出△ABC关于直线L的对称图形,标注字母并简要说明.
???
18、点A(-l,4)和点B(-5,1)在平面直角坐标系中的位置如图所示.?????
???
(1)将点A、B分别向右平移5个单位,得到点A1、B1,请画出四边形AA1B1B;
(2)画一条直线,将四边形AA1B1B分成两个全等的图形,并且每个图形都是轴对称图形.
19、△ABC在直角坐标系中的位置如图所示,其中A(﹣3,5),B(﹣5,2),C(﹣1,3),直线l经过点(0,1),并且与x轴平行,△A′B′C′与△ABC关于线1对称.
(1)画出△A′B′C′,并写出△A′B′C′三个顶点的坐标: ??
;
(2)观察图中对应点坐标之间的关系,写出点P(a,b)关于直线l的对称点P′的坐标: ??
;
(3)若直线l′经过点(0,m),并且与x轴平行,根据上面研究的经验,写出点Q(c,d)关于直线1′的对称点Q′的坐标: ??
.
20、在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
21、如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=lcm,∠BAC=76°,∠EAC=58°
(1)求出BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系?
参考答案
一、选择题
1、C
2、A?
3、B
4、D??
5、D.解:∵直线m上各点的横坐标都是2,
∴直线为:x=2,
∵点P(a,5)在第二象限,
∴a到2的距离为:2﹣a,
∴点P关于直线m对称的点的横坐标是:2﹣a+2=4﹣a,
故P点对称的点的坐标是:(﹣a+4,5).
6、B.解:∵点A(m,3)与点B(4,n)关于y轴对称,
∴m=﹣4,n=3,
∴(m+n)2019=(﹣4+3)2019=﹣1,
二、填空题
9、21
10、对称轴上??
11、﹣2<a<3
【解答】解:∵P关于x轴的对称点在第四象限内,
∴点P位于第一象限.
∴3a+6>0①,3﹣a>0②.
解不等式①得:a>﹣2,
解不等式②得:a<3,
所以a的取值范围是:﹣2<a<3.
故答案为:﹣2<a<3.
12、BA629 点拨:假定最左侧或右侧有一条直线为对称轴,沿此直线折叠都会得到BA629,或将此图案从反面观察,也可得到BA629.
13、(-1,1)或(-2,-2)
14、一2
15、(﹣a,b)解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2019÷4=504余3,
∴经过第2019次变换后所得的A点与第三次变换的位置相同,在第二象限,坐标为(﹣a,b).
三、解答题
16、解:如下图
17、解:如图所示,
即为所求.
?
18、解:(1)如图,A、B两点、连线得四边形AA1B1B.
(2)如图,画一条直线A
B1或B
A1即可.
四、解答题
19、【解答】解:(1)如图所示,△A′B′C′即为所求,A'(﹣3,﹣3),B'(﹣5,0),C'(﹣1,﹣1);
故答案为:A'(﹣3,﹣3),B'(﹣5,0),C'(﹣1,﹣1);
(2)由题可得,点P'的横坐标为a,
设点P'的纵坐标为y,则=1,
解得y=2﹣b,
∴点P(a,b)关于直线l的对称点P′的坐标为(a,2﹣b),
故答案为:(a,2﹣b);
(3)由题可得,点Q′的横坐标为c,
设点Q'的纵坐标为y,则=m,
解得y=2m﹣d,
∴点Q(c,d)关于直线1′的对称点Q′的坐标为(c,2m﹣d).
故答案为:(c,2m﹣d).
20、【考点】作图-轴对称变换.
【分析】(1)根据顶点A,C的坐标分别为(﹣4,5),(﹣1,3)建立坐标系即可;
(2)作出各点关于y轴的对称点,再顺次连接即可;
(3)根据点B′在坐标系中的位置写出其坐标即可.
【解答】解:(1)如图所示;
(2)如图所示;
(3)由图可知,B′(2,1).
【点评】本题考查的是作图﹣轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.
21、【解答】解:(1)∵△ABC与△ADE关于直线MN对称,ED=4cm,FC=1cm,
∴BC=ED=4cm,
∴BF=BC﹣FC=3cm.
(2)∵△ABC与△ADE关于直线MN对称,∠BAC=76°,∠EAC=58°,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD﹣∠EAC=76°﹣58°=18°.
(3)结论:直线MN垂直平分线段EC.理由如下:
∵E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
