2010-2011学年番禺区高二数学水平测试必修2(a组)训练题
文档属性
| 名称 | 2010-2011学年番禺区高二数学水平测试必修2(a组)训练题 |

|
|
| 格式 | zip | ||
| 文件大小 | 101.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-25 00:00:00 | ||
图片预览

文档简介
2010-2011学年番禺区高二数学水平测试必修2(A组)训练题
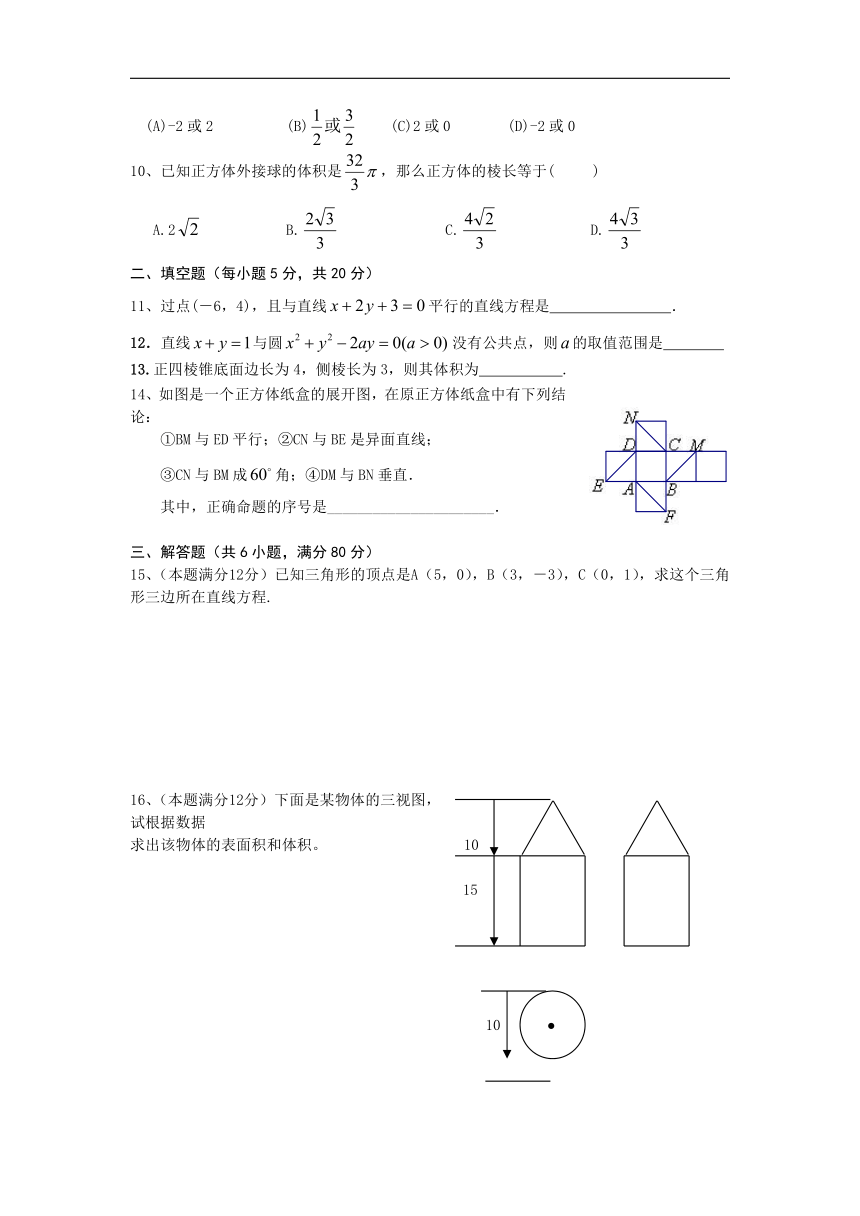
命题人:许红艳 审题人:张婷
一、选择题(每小题5分,共50分)
1、经过点的直线的斜率为( )
2、若三点A(-1,0),B(2,3),C(0,m)共线,则m的值为( )
A.1 B. -1 C. D.2
3、倾斜角为135,在轴上的截距为的直线方程是( )
A. B. C. D.
4、若方程表示圆,则实数m的取值范围是( )
5、两圆的方程是(x+1)2+(y-1)2=36,x2+y2-4x+2y+4=0,则两圆的位置关系为( )
A.相交 B.内含 C.外切 D.内切
6、给出下列命题:
垂直于同一直线的两直线平行.
同平行于一平面的两直线平行.
同平行于一直线的两直线平行.
平面内不相交的两直线平行.
其中正确的命题个数是( )
(A) 1 (B) 2 (C) 3 (D) 4
7、下列四个命题中,假命题是( )
A.若平面 内有两条相交直线与平面 内的两条相交直线分别平行,则 ∥
B.平行于同一平面的两个平面平行
C.如果平面 内有无数条直线都与平面 平行,则 ∥
D.如果平面 内任意一条直线都与平面 平行,则 ∥
8、如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
(A)BD∥平面CB1D1 (B)AC1⊥BD
(C)AC1⊥平面CB1D1 (D)异面直线AD1与CB所成的角为60°
9、若圆的圆心到直线的距离为,则a的值为( )
(A)-2或2 (B) (C)2或0 (D)-2或0
10、已知正方体外接球的体积是,那么正方体的棱长等于( )
A.2 B. C. D.
二、填空题(每小题5分,共20分)
11、过点(-6,4),且与直线平行的直线方程是 .
12.直线与圆没有公共点,则的取值范围是
13.正四棱锥底面边长为4,侧棱长为3,则其体积为 .
14、如图是一个正方体纸盒的展开图,在原正方体纸盒中有下列结论:
①BM与ED平行;②CN与BE是异面直线;
③CN与BM成角;④DM与BN垂直.
其中,正确命题的序号是______________________.
三、解答题(共6小题,满分80分)
15、(本题满分12分)已知三角形的顶点是A(5,0),B(3,-3),C(0,1),求这个三角形三边所在直线方程.
16、(本题满分12分)下面是某物体的三视图,
试根据数据
求出该物体的表面积和体积。 10
15
10
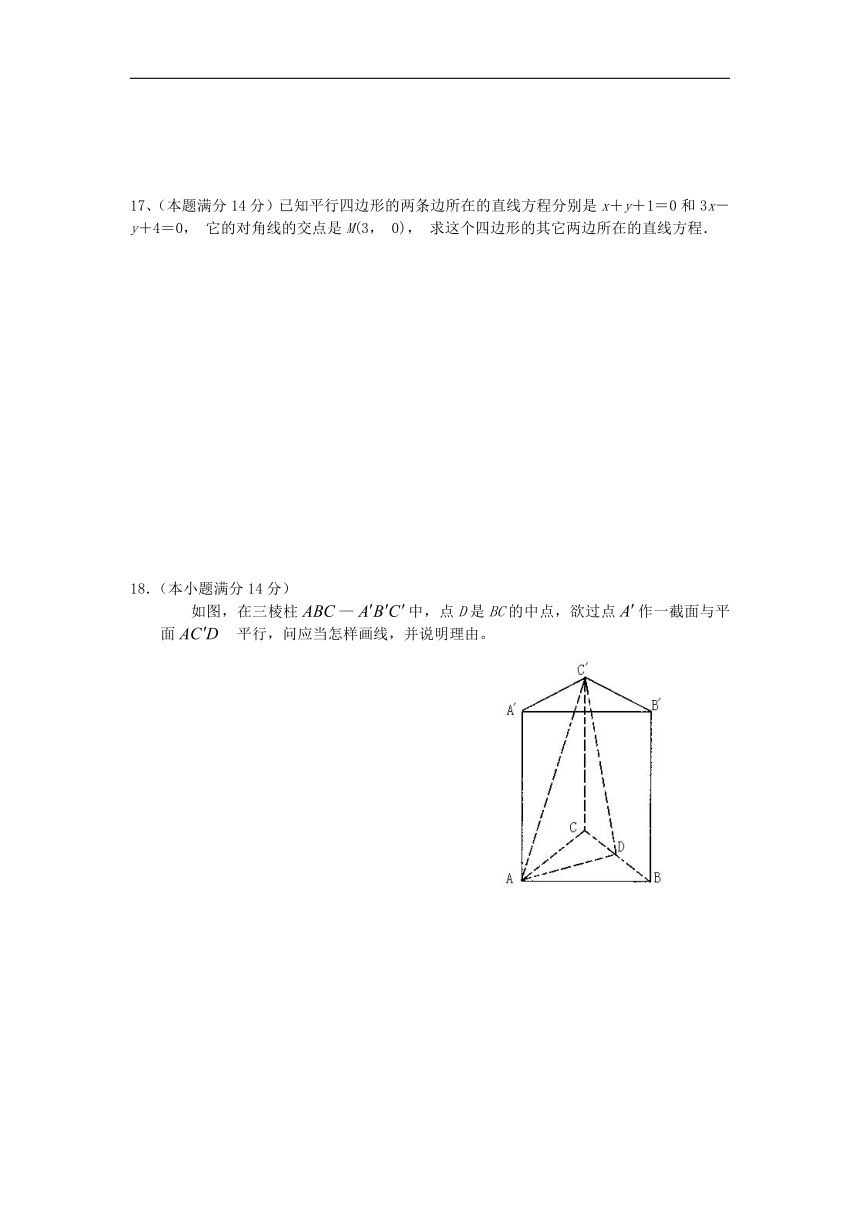
17、(本题满分14分)已知平行四边形的两条边所在的直线方程分别是x+y+1=0和3x-y+4=0, 它的对角线的交点是M(3, 0), 求这个四边形的其它两边所在的直线方程.
18.(本小题满分14分)
如图,在三棱柱—中,点D是BC的中点,欲过点作一截面与平面 平行,问应当怎样画线,并说明理由。
19、(本题满分14分)求过点A(2,-3),B(―2,―5),且圆心在直线x-2y-3=0上的圆的方程
20、(本题满分14分)已知圆C: ,直线.
(1)b为何值时直线和圆相切,并求出切点坐标;
(2)b为何值时直线和圆相交,并求出弦长.
高二数学水平测试(必修2)训练题A答案
选择题:BADAB BCDCD
二、11、;12、;13、;14、③④
三、解答题:15、答案:AB所在直线方程为,直线BC的方程为,直线AC的方程为。(说明:本题有多种解法。)
16、解:由三视图知,该物体是由下部分为底面直径为10、高位15的圆柱,上部分是底面直径为10高为10的圆椎组成的。
表面积== 体积=
x+y+1=0
17、解:由 的相邻两条边的交点为,
3x-y+4=0
又对角线的交点为M(3, 0),另两条边的交点为,且斜率分别为-1和3,由点斜式知所求两条直线的方程为和
18.(本小题满分14分)
解:(Ⅰ)取的中点E,连结,
则平面∥平面
∵D为BC的中点,E为的中点,∴
又∵BC∥,∴四边形为平行四边形,
∴∥BE,
连结DE,则DE,
∴DE,
∴四边形是平行四边形,
∴AD∥
又∵ 平面,,∴平面∥平面。
19、解:设所求圆的方程为.
有条件知
解得 所求圆的方程为
20、解: 得
判别式.
当时,,直线和圆相切.因为切点一定在直线上,所以切点坐标为或
当,即时,直线和圆相交.
因为圆心到直线的距离为,所以割线长为
MACROBUTTON MTEditEquationSection2 Equation Chapter 1 Section 1 SEQ MTEqn \r \h \* MERGEFORMAT SEQ MTSec \r 1 \h \* MERGEFORMAT SEQ MTChap \r 1 \h \* MERGEFORMAT EMBED Equation.DSMT4
命题人:许红艳 审题人:张婷
一、选择题(每小题5分,共50分)
1、经过点的直线的斜率为( )
2、若三点A(-1,0),B(2,3),C(0,m)共线,则m的值为( )
A.1 B. -1 C. D.2
3、倾斜角为135,在轴上的截距为的直线方程是( )
A. B. C. D.
4、若方程表示圆,则实数m的取值范围是( )
5、两圆的方程是(x+1)2+(y-1)2=36,x2+y2-4x+2y+4=0,则两圆的位置关系为( )
A.相交 B.内含 C.外切 D.内切
6、给出下列命题:
垂直于同一直线的两直线平行.
同平行于一平面的两直线平行.
同平行于一直线的两直线平行.
平面内不相交的两直线平行.
其中正确的命题个数是( )
(A) 1 (B) 2 (C) 3 (D) 4
7、下列四个命题中,假命题是( )
A.若平面 内有两条相交直线与平面 内的两条相交直线分别平行,则 ∥
B.平行于同一平面的两个平面平行
C.如果平面 内有无数条直线都与平面 平行,则 ∥
D.如果平面 内任意一条直线都与平面 平行,则 ∥
8、如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
(A)BD∥平面CB1D1 (B)AC1⊥BD
(C)AC1⊥平面CB1D1 (D)异面直线AD1与CB所成的角为60°
9、若圆的圆心到直线的距离为,则a的值为( )
(A)-2或2 (B) (C)2或0 (D)-2或0
10、已知正方体外接球的体积是,那么正方体的棱长等于( )
A.2 B. C. D.
二、填空题(每小题5分,共20分)
11、过点(-6,4),且与直线平行的直线方程是 .
12.直线与圆没有公共点,则的取值范围是
13.正四棱锥底面边长为4,侧棱长为3,则其体积为 .
14、如图是一个正方体纸盒的展开图,在原正方体纸盒中有下列结论:
①BM与ED平行;②CN与BE是异面直线;
③CN与BM成角;④DM与BN垂直.
其中,正确命题的序号是______________________.
三、解答题(共6小题,满分80分)
15、(本题满分12分)已知三角形的顶点是A(5,0),B(3,-3),C(0,1),求这个三角形三边所在直线方程.
16、(本题满分12分)下面是某物体的三视图,
试根据数据
求出该物体的表面积和体积。 10
15
10
17、(本题满分14分)已知平行四边形的两条边所在的直线方程分别是x+y+1=0和3x-y+4=0, 它的对角线的交点是M(3, 0), 求这个四边形的其它两边所在的直线方程.
18.(本小题满分14分)
如图,在三棱柱—中,点D是BC的中点,欲过点作一截面与平面 平行,问应当怎样画线,并说明理由。
19、(本题满分14分)求过点A(2,-3),B(―2,―5),且圆心在直线x-2y-3=0上的圆的方程
20、(本题满分14分)已知圆C: ,直线.
(1)b为何值时直线和圆相切,并求出切点坐标;
(2)b为何值时直线和圆相交,并求出弦长.
高二数学水平测试(必修2)训练题A答案
选择题:BADAB BCDCD
二、11、;12、;13、;14、③④
三、解答题:15、答案:AB所在直线方程为,直线BC的方程为,直线AC的方程为。(说明:本题有多种解法。)
16、解:由三视图知,该物体是由下部分为底面直径为10、高位15的圆柱,上部分是底面直径为10高为10的圆椎组成的。
表面积== 体积=
x+y+1=0
17、解:由 的相邻两条边的交点为,
3x-y+4=0
又对角线的交点为M(3, 0),另两条边的交点为,且斜率分别为-1和3,由点斜式知所求两条直线的方程为和
18.(本小题满分14分)
解:(Ⅰ)取的中点E,连结,
则平面∥平面
∵D为BC的中点,E为的中点,∴
又∵BC∥,∴四边形为平行四边形,
∴∥BE,
连结DE,则DE,
∴DE,
∴四边形是平行四边形,
∴AD∥
又∵ 平面,,∴平面∥平面。
19、解:设所求圆的方程为.
有条件知
解得 所求圆的方程为
20、解: 得
判别式.
当时,,直线和圆相切.因为切点一定在直线上,所以切点坐标为或
当,即时,直线和圆相交.
因为圆心到直线的距离为,所以割线长为
MACROBUTTON MTEditEquationSection2 Equation Chapter 1 Section 1 SEQ MTEqn \r \h \* MERGEFORMAT SEQ MTSec \r 1 \h \* MERGEFORMAT SEQ MTChap \r 1 \h \* MERGEFORMAT EMBED Equation.DSMT4
同课章节目录
