六年级下册数学课件-三 正比例和反比例 复习课件 西师大版 (共13张PPT)
文档属性
| 名称 | 六年级下册数学课件-三 正比例和反比例 复习课件 西师大版 (共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 486.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-27 12:29:40 | ||
图片预览





文档简介
三 正比例和反比例 复习课件
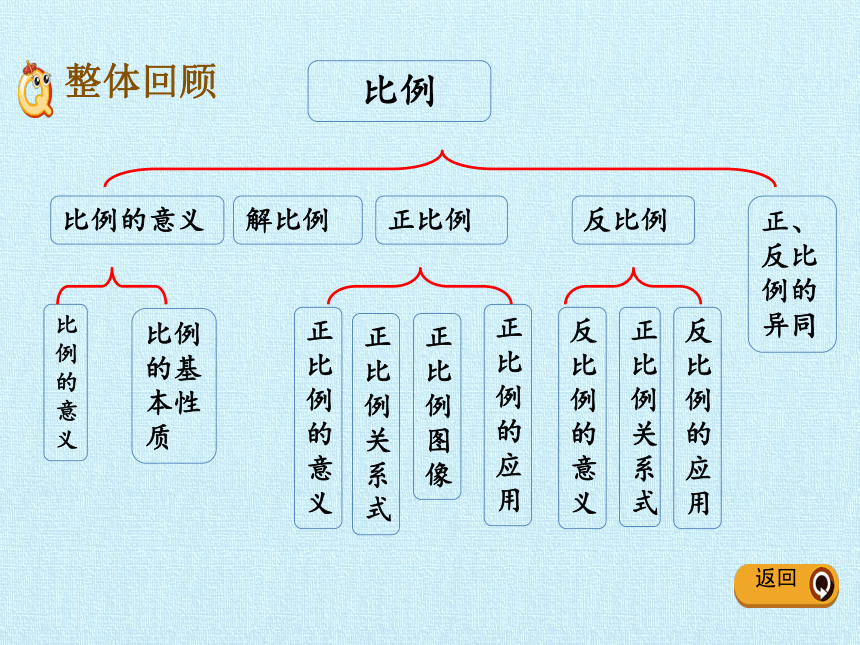
比例
比例的意义
比例的意义
比例的基本性质
正比例的意义
正比例的应用
正比例
解比例
反比例
正比例图像
反比例的意义
反比例的应用
正比例关系式
正比例关系式
正、反比例的异同
整体回顾
返回
1.比例的意义
表示两个比相等的式子,叫比例。
在一个比例中,两个外项的积,等于两个内项的积, 这叫做比例的基本性质。
2.比例的基本性质
3.解比例
根据比例的基本性质求比例中的未知项叫做解比例。
知识梳理
返回
4.正比例的意义
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
=k(一定)。
5.正比例关系式
返回
6.正比例图像
表示成正比例关系的两种量中相对应的各点在同一条直线上,即正比例关系的图条经过原点的直线。
从图像中可以直观地看出两种量的变化情况。
借助图像,可以由一个量的值找到对应的另一个量的值。
返回
7.反比例的意义
8.正比例关系式
成反比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
x·y=k(一定)
返回
返回
1.都是两种相关联的量
相同点:
1.变化方向相同,一种量扩大或缩小,另一种量也扩大或缩小
2.一种量随着另一种量的变化而变化。
不同点:
1.变化方向相反,一种量扩大或缩小,另一种量反而缩小或扩大。
2.相对应的两个数的比值一定。
正比例:
反比例:
2.相对应的两个数的乘积定
3.关系式: =k(一定)
3.关系式:x·y=k(一定)
9.正、反比例的异同
长2.4m,宽1.6m 长60cm,宽40cm
(1)这两个长方形的长和宽的比,是否可以组成比例?
(2)如果可以组成比例,把组成的比例写出来,并指出这个比例的内项和外项。
长和宽的比:
2.4:1.6
60:40
可以组成比例
2.4 : 1.6 = 60 : 40
内项
外项
综合运用
返回
(4) :=x:
(3) =
解比例。
(1)10:12=x:30 (2)2x:0.8=1.5:4
解:12x=10×30
x=300÷12
x=25
解:2x×4=0.8×1.5
8x=1.2
χ=0.15
x=1.2÷8
解:2x=1.8×5
x=9÷2
x=4.5
解:×x= ×
x= ÷
x=
返回
(1)学校举行方阵团体操表演,排成5列需要90人。照这样计算,排成24列,需要多少人
(2)学校举行方阵团体操表演,如果每列16人,要排27列。
(1)90÷5×24
=18×24
=432(人)
(2)解:设要排x列。
18x=16×27
x=432÷18
x=24
答:要排24列。
答:需要432人。
返回
一架飞机的飞行时间和航程如下表:
飞行时间(时)
2
3
4
6
航程(km)
1600
2400
3200
4800
(1)写出几组航程和相对应的飞行时间的比,并比较比值的大小。说一说它们的比值表示什么。
(2)表中的航程和飞行时间成正比例吗?为什么?
=800
=800
=800
=800
比值表示航行的速度
成正比例。
因为航程和时间的比值一定(800),所以成正比例。
返回
一架飞机的飞行时间和航程如下表。
(3)在下图中描出表示航程和相应飞行时间的点,然后把它们顺次连起来并估计一下飞行2500km要用多长时间?
●
●
●
●
飞行时间(时)
2
3
4
6
航程(km)
1600
2400
3200
4800
返回
谢 谢
比例
比例的意义
比例的意义
比例的基本性质
正比例的意义
正比例的应用
正比例
解比例
反比例
正比例图像
反比例的意义
反比例的应用
正比例关系式
正比例关系式
正、反比例的异同
整体回顾
返回
1.比例的意义
表示两个比相等的式子,叫比例。
在一个比例中,两个外项的积,等于两个内项的积, 这叫做比例的基本性质。
2.比例的基本性质
3.解比例
根据比例的基本性质求比例中的未知项叫做解比例。
知识梳理
返回
4.正比例的意义
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
=k(一定)。
5.正比例关系式
返回
6.正比例图像
表示成正比例关系的两种量中相对应的各点在同一条直线上,即正比例关系的图条经过原点的直线。
从图像中可以直观地看出两种量的变化情况。
借助图像,可以由一个量的值找到对应的另一个量的值。
返回
7.反比例的意义
8.正比例关系式
成反比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
x·y=k(一定)
返回
返回
1.都是两种相关联的量
相同点:
1.变化方向相同,一种量扩大或缩小,另一种量也扩大或缩小
2.一种量随着另一种量的变化而变化。
不同点:
1.变化方向相反,一种量扩大或缩小,另一种量反而缩小或扩大。
2.相对应的两个数的比值一定。
正比例:
反比例:
2.相对应的两个数的乘积定
3.关系式: =k(一定)
3.关系式:x·y=k(一定)
9.正、反比例的异同
长2.4m,宽1.6m 长60cm,宽40cm
(1)这两个长方形的长和宽的比,是否可以组成比例?
(2)如果可以组成比例,把组成的比例写出来,并指出这个比例的内项和外项。
长和宽的比:
2.4:1.6
60:40
可以组成比例
2.4 : 1.6 = 60 : 40
内项
外项
综合运用
返回
(4) :=x:
(3) =
解比例。
(1)10:12=x:30 (2)2x:0.8=1.5:4
解:12x=10×30
x=300÷12
x=25
解:2x×4=0.8×1.5
8x=1.2
χ=0.15
x=1.2÷8
解:2x=1.8×5
x=9÷2
x=4.5
解:×x= ×
x= ÷
x=
返回
(1)学校举行方阵团体操表演,排成5列需要90人。照这样计算,排成24列,需要多少人
(2)学校举行方阵团体操表演,如果每列16人,要排27列。
(1)90÷5×24
=18×24
=432(人)
(2)解:设要排x列。
18x=16×27
x=432÷18
x=24
答:要排24列。
答:需要432人。
返回
一架飞机的飞行时间和航程如下表:
飞行时间(时)
2
3
4
6
航程(km)
1600
2400
3200
4800
(1)写出几组航程和相对应的飞行时间的比,并比较比值的大小。说一说它们的比值表示什么。
(2)表中的航程和飞行时间成正比例吗?为什么?
=800
=800
=800
=800
比值表示航行的速度
成正比例。
因为航程和时间的比值一定(800),所以成正比例。
返回
一架飞机的飞行时间和航程如下表。
(3)在下图中描出表示航程和相应飞行时间的点,然后把它们顺次连起来并估计一下飞行2500km要用多长时间?
●
●
●
●
飞行时间(时)
2
3
4
6
航程(km)
1600
2400
3200
4800
返回
谢 谢
