五年级上册数学课件-二 图形的平移、旋转与轴对称 复习课件 西师大版 (共54张PPT)
文档属性
| 名称 | 五年级上册数学课件-二 图形的平移、旋转与轴对称 复习课件 西师大版 (共54张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-27 00:00:00 | ||
图片预览








文档简介
二 图形的平移、旋转与轴对称
复习课件
图形的平移、旋转与轴对称
图形平移的方法
画出平移后的图形
描述旋转方向与旋转角度
按要求画出物体旋转后的图形
对称轴
画出图形的另一半
用图形的平移、旋转设计图案
用图形的轴对称设计图案
复习旧知
这组图案是怎样得到的?
通过平移得到的。
像这样,物体或图形沿着某一方向做直线运动的现象叫平移。
物体或图形都是沿着直线运动,且运动时物体的大小、形状、方向没有发生改变,只是位置发生了变化。
平移的特征
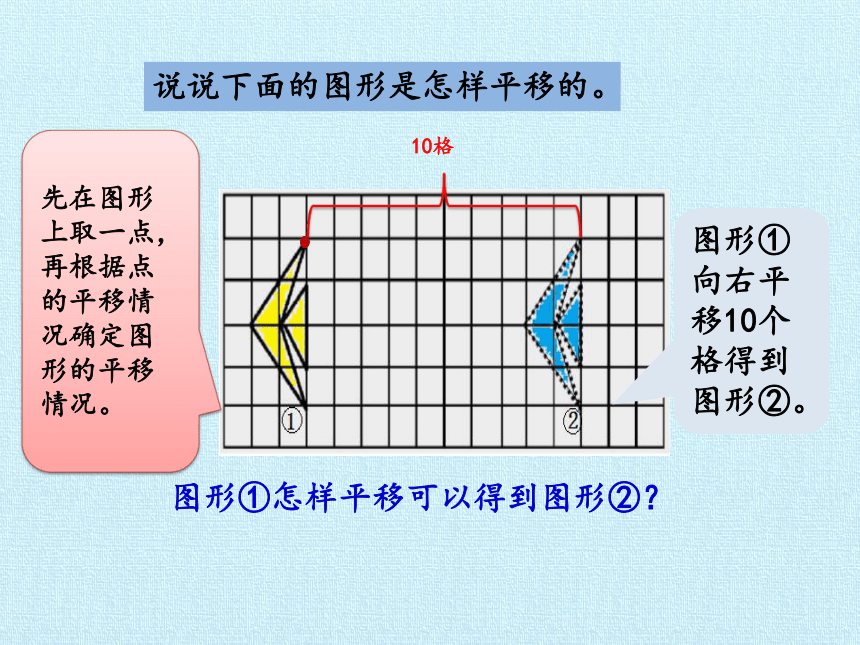
说说下面的图形是怎样平移的。
图形①怎样平移可以得到图形②?
先在图形上取一点,再根据点的平移情况确定图形的平移情况。
10格
图形①向右平移10个格得到图形②。
画平移图形的方法是什么?
1.找出原图形的关键点(图形的顶点)。
2.把要平移图形的各个顶点按指定的方向和格子数平移到新位置,描出各点。
3.把各点按原图形的顺序依次连接起来。
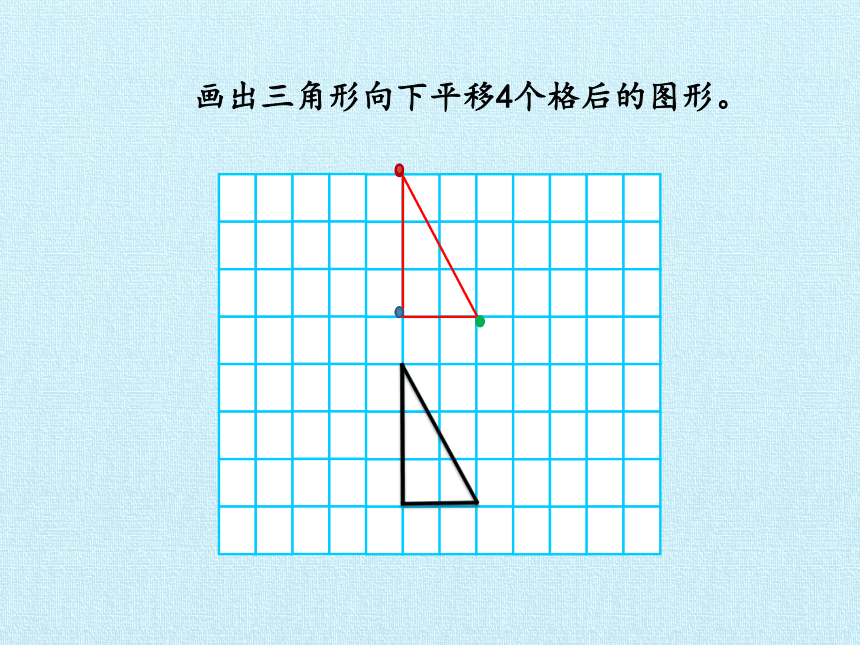
画出三角形向下平移4个格后的图形。
巩固练习
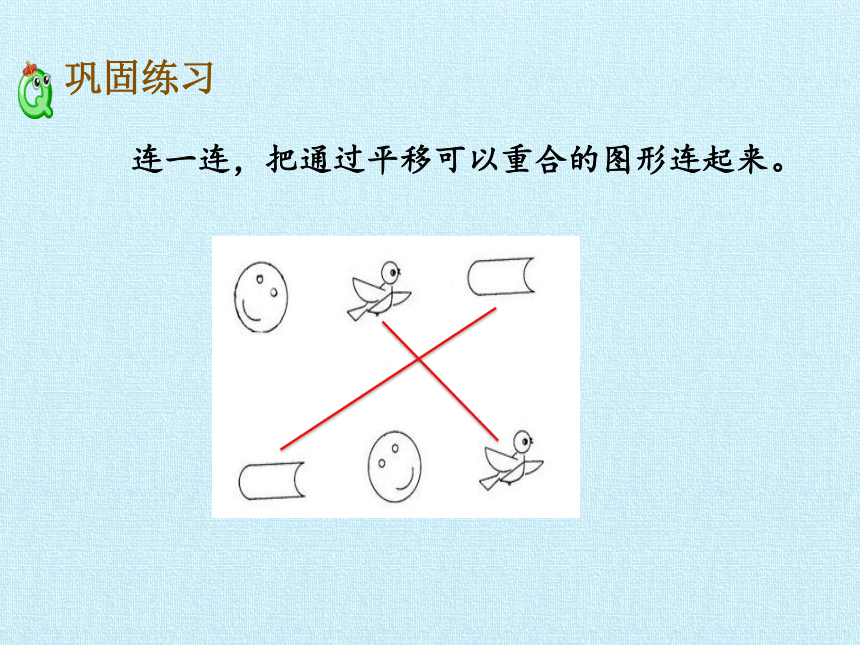
连一连,把通过平移可以重合的图形连起来。
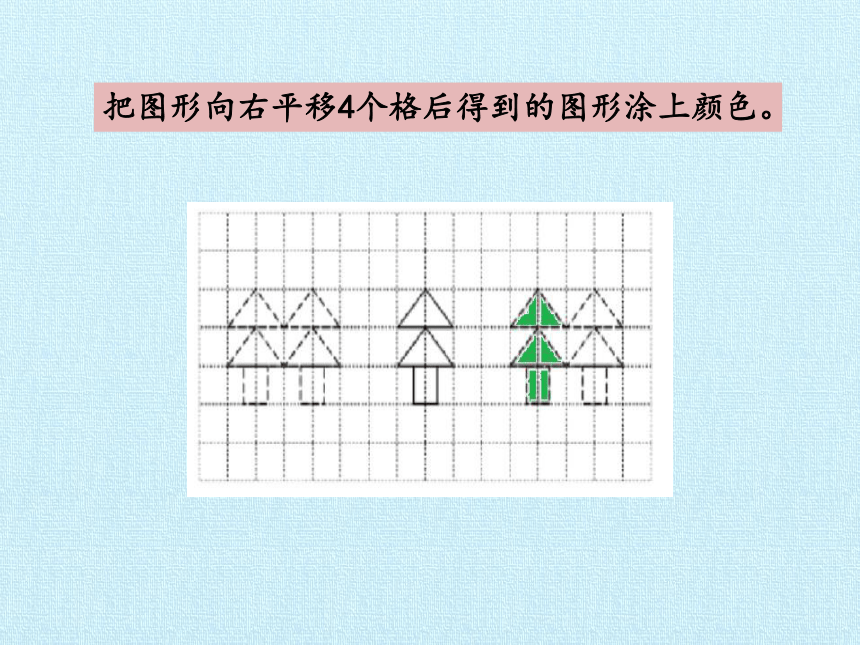
把图形向右平移4个格后得到的图形涂上颜色。
小结1
平移是图形或物体做直线运动的现象。
平移前后,物体的形状、大小、方向都没有改变,只有位置变了。
小结1
画平移图形的方法:
1.找出原图形的关键点(图形的顶点)。
2.把要平移图形的各个顶点按指定的方向和格子数平移到新位置,描出各点。
3.把各点按原图形的顺序依次链接起来。
复习旧知
生
活
中
的
旋
转
什么是旋转?
旋转是物体或图形围绕一个点或一个轴运动。
旋转方向
与时针旋转的方向相同,通常叫顺时针方向旋转。
指针从A旋转到D,顺时针旋转了90°。
与时针旋转的方向相反,通常叫逆时针方向旋转。
指针从A旋转到B,逆时针旋转了90°。
旋转角度
如何确定一个物体或图形旋转的角度?
可以对图形中的某一条线段进行观察,看旋转后这条线段的位置与原来的位置发生了什么变化,这样来确定图形旋转的角度。
如何画出简单的旋转图形?
第一:明确画图要求。(旋转点、旋转方向、旋转角度。)
第二:画图。找出图形中关键的线段,按要求旋转,画出旋转后的,然后根据图形的特点画出图形。
1.下面是旋转现象的是( )。
2.下面各图中,图形B是图形A绕点O顺时针旋转90°得到的是( )。
A
C
巩固练习
小结2
1.图形旋转前后形状、大小不变,位置和方向发生改变。
2.可以对图形中的某一条线段进行观察,看旋转后这条线段的位置与原来的位置发生了什么变化,这样来确定图形旋转的角度。
复习旧知
这类图形有什么共同的特征?
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
折痕所在的这条直线叫做对称轴。
在轴对称图形中, 折痕所在的直线就是这个图形的对称轴。
对称轴
等腰三角形
等边三角形
一条
三条
×
√
√
菱形
两条
√
×
有的轴对称图形有1条对称轴,有的不止1条。
利用轴对称的知识画一个正方形。
第一步:确定对称轴的位置。
第二步:根据对称轴,找到对应点。
第三步:把各点顺次连接起来,得到轴对称图形。
巩固练习
选一选。
1.下列图形中:等腰三角形、圆、直角三角形、等腰梯形、长方形,其中一定是轴对称图形的有( )个。
A.2 B.3 C.4 D.5
2.下面不是轴对称图形的是( )。
A.正方形 B.平行四边形 C.半圆 D.线段
C
B
小结3
1.轴对称图形沿一条直线对折后,两部分能完全重合,折痕所在直线叫做对称轴。
2.在轴对称图形中,有的只有1条对称轴,有的不止1条对称轴。
小结3
3.画对称轴时,可以用对折的方法将图形对折后,画出对称轴;当图形不能对折时,根据图形的特点进行判断,画出对称轴。
4.画轴对称图形的方法:先找出对称轴的位置,再根据对称轴找出对应点,最后把各点连起来,就得到一个轴对称图形。
复习旧知
回忆一下你都运用过哪些方法设计美丽的图案。
平移、旋转、轴对称。
说说美丽的图案是怎样得到的。
1.一个图案可以通过三种变换方式中的一种或两种甚至三种得到。
2.复杂、美丽的图案可以用一个简单图形经过平移、旋转或对称得到。
1.下面的图案是通过( )得到的。
观察图形,以三角形为基本图形每次向右平移2格,得到的。
平移
巩固练习
2.下图是由①通过( )得到的。
观察图形,由原图形①顺时针旋转90°得到②,依次类推。
旋转
3.观察方格纸上所画图形的位置关系,并填空。
图形B可以看作图形A绕点O顺时针方向旋转( )得到的。图形C可以看作图形B绕点O( )方向旋转90°得到的。图形D可以看作图形C绕点( )顺时针方向旋转90°得到的。
90°
顺时针
O
4.下图中,从左图变化到右图,先( ),再( )即可。
旋转【或对称】
平移【或对称】
5.
(1)从6:00到9:00时针旋转了( )°。
(2)如图:阀门手柄绕O点( )时针旋转了90°。
90
逆
6.下面的现象中是平移的画△,是旋转的画○。
(1)推拉窗的移动。( )
(2)飞机的螺旋桨。( )
(3)索道上运行的观光缆车。( )
(4)拉动抽屉。( )
(5)钟面上分针的转动。( )
(6)工作中的电风扇。( )
△
○
△
△
○
○
7.利用平移设计美丽的图案。
我根据平移的特征,把这条“小鱼”各顶点向右平移4格,再4格……
8.利用旋转设计美丽的图案。
根据旋转的特征,小旗子绕点O顺(或逆)时针旋转90°,再旋转90°即可成为一幅美丽的图案。
9.利用轴对称设计美丽的图案。
先确定对称轴,以已知图形的最右边所在的直线为对称轴,根据轴对称图形的性质,在对称轴的右边画出已知图形的关键的对称点,然后连接即可得到轴对称图案。
小结4
一个简单的图形经过平移、旋转或对称的变换即可得到复杂、美丽的图案。
找图形的变化规律和计算图中的个数问题时,我们应注意什么?
1.找图形的变化规律时,要充分考虑到平移和旋转的特征。
2.解决下幅图的个数问题时,可以按照规律继续画一画,也可以用算式计算。
复习旧知
1.按规律接着画两个。
巩固练习
通过观察可以看出,三角形是按照顺时针方向依次旋转90°。
2.舞台上有15只小熊参加表演,一共多少条腿着地?
后面的小熊都是两条腿着地。
通过观察可知,第一只小熊4条腿着地,后面的小熊2条腿着地,因此共有:
4+2×(15-1)
=4+2×14
=32(条)
答:共有32条腿着地。
3.找出规律,接着画。
由题意可知:图形在方格中进行顺时针旋转,据此画图即可。
小结5
1.找图形的变化规律时,要充分考虑平移和旋转的特征。
2.解决下幅图的个数问题时,可以按照规律继续画一画,也可以用算式计算。
谢 谢
复习课件
图形的平移、旋转与轴对称
图形平移的方法
画出平移后的图形
描述旋转方向与旋转角度
按要求画出物体旋转后的图形
对称轴
画出图形的另一半
用图形的平移、旋转设计图案
用图形的轴对称设计图案
复习旧知
这组图案是怎样得到的?
通过平移得到的。
像这样,物体或图形沿着某一方向做直线运动的现象叫平移。
物体或图形都是沿着直线运动,且运动时物体的大小、形状、方向没有发生改变,只是位置发生了变化。
平移的特征
说说下面的图形是怎样平移的。
图形①怎样平移可以得到图形②?
先在图形上取一点,再根据点的平移情况确定图形的平移情况。
10格
图形①向右平移10个格得到图形②。
画平移图形的方法是什么?
1.找出原图形的关键点(图形的顶点)。
2.把要平移图形的各个顶点按指定的方向和格子数平移到新位置,描出各点。
3.把各点按原图形的顺序依次连接起来。
画出三角形向下平移4个格后的图形。
巩固练习
连一连,把通过平移可以重合的图形连起来。
把图形向右平移4个格后得到的图形涂上颜色。
小结1
平移是图形或物体做直线运动的现象。
平移前后,物体的形状、大小、方向都没有改变,只有位置变了。
小结1
画平移图形的方法:
1.找出原图形的关键点(图形的顶点)。
2.把要平移图形的各个顶点按指定的方向和格子数平移到新位置,描出各点。
3.把各点按原图形的顺序依次链接起来。
复习旧知
生
活
中
的
旋
转
什么是旋转?
旋转是物体或图形围绕一个点或一个轴运动。
旋转方向
与时针旋转的方向相同,通常叫顺时针方向旋转。
指针从A旋转到D,顺时针旋转了90°。
与时针旋转的方向相反,通常叫逆时针方向旋转。
指针从A旋转到B,逆时针旋转了90°。
旋转角度
如何确定一个物体或图形旋转的角度?
可以对图形中的某一条线段进行观察,看旋转后这条线段的位置与原来的位置发生了什么变化,这样来确定图形旋转的角度。
如何画出简单的旋转图形?
第一:明确画图要求。(旋转点、旋转方向、旋转角度。)
第二:画图。找出图形中关键的线段,按要求旋转,画出旋转后的,然后根据图形的特点画出图形。
1.下面是旋转现象的是( )。
2.下面各图中,图形B是图形A绕点O顺时针旋转90°得到的是( )。
A
C
巩固练习
小结2
1.图形旋转前后形状、大小不变,位置和方向发生改变。
2.可以对图形中的某一条线段进行观察,看旋转后这条线段的位置与原来的位置发生了什么变化,这样来确定图形旋转的角度。
复习旧知
这类图形有什么共同的特征?
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
折痕所在的这条直线叫做对称轴。
在轴对称图形中, 折痕所在的直线就是这个图形的对称轴。
对称轴
等腰三角形
等边三角形
一条
三条
×
√
√
菱形
两条
√
×
有的轴对称图形有1条对称轴,有的不止1条。
利用轴对称的知识画一个正方形。
第一步:确定对称轴的位置。
第二步:根据对称轴,找到对应点。
第三步:把各点顺次连接起来,得到轴对称图形。
巩固练习
选一选。
1.下列图形中:等腰三角形、圆、直角三角形、等腰梯形、长方形,其中一定是轴对称图形的有( )个。
A.2 B.3 C.4 D.5
2.下面不是轴对称图形的是( )。
A.正方形 B.平行四边形 C.半圆 D.线段
C
B
小结3
1.轴对称图形沿一条直线对折后,两部分能完全重合,折痕所在直线叫做对称轴。
2.在轴对称图形中,有的只有1条对称轴,有的不止1条对称轴。
小结3
3.画对称轴时,可以用对折的方法将图形对折后,画出对称轴;当图形不能对折时,根据图形的特点进行判断,画出对称轴。
4.画轴对称图形的方法:先找出对称轴的位置,再根据对称轴找出对应点,最后把各点连起来,就得到一个轴对称图形。
复习旧知
回忆一下你都运用过哪些方法设计美丽的图案。
平移、旋转、轴对称。
说说美丽的图案是怎样得到的。
1.一个图案可以通过三种变换方式中的一种或两种甚至三种得到。
2.复杂、美丽的图案可以用一个简单图形经过平移、旋转或对称得到。
1.下面的图案是通过( )得到的。
观察图形,以三角形为基本图形每次向右平移2格,得到的。
平移
巩固练习
2.下图是由①通过( )得到的。
观察图形,由原图形①顺时针旋转90°得到②,依次类推。
旋转
3.观察方格纸上所画图形的位置关系,并填空。
图形B可以看作图形A绕点O顺时针方向旋转( )得到的。图形C可以看作图形B绕点O( )方向旋转90°得到的。图形D可以看作图形C绕点( )顺时针方向旋转90°得到的。
90°
顺时针
O
4.下图中,从左图变化到右图,先( ),再( )即可。
旋转【或对称】
平移【或对称】
5.
(1)从6:00到9:00时针旋转了( )°。
(2)如图:阀门手柄绕O点( )时针旋转了90°。
90
逆
6.下面的现象中是平移的画△,是旋转的画○。
(1)推拉窗的移动。( )
(2)飞机的螺旋桨。( )
(3)索道上运行的观光缆车。( )
(4)拉动抽屉。( )
(5)钟面上分针的转动。( )
(6)工作中的电风扇。( )
△
○
△
△
○
○
7.利用平移设计美丽的图案。
我根据平移的特征,把这条“小鱼”各顶点向右平移4格,再4格……
8.利用旋转设计美丽的图案。
根据旋转的特征,小旗子绕点O顺(或逆)时针旋转90°,再旋转90°即可成为一幅美丽的图案。
9.利用轴对称设计美丽的图案。
先确定对称轴,以已知图形的最右边所在的直线为对称轴,根据轴对称图形的性质,在对称轴的右边画出已知图形的关键的对称点,然后连接即可得到轴对称图案。
小结4
一个简单的图形经过平移、旋转或对称的变换即可得到复杂、美丽的图案。
找图形的变化规律和计算图中的个数问题时,我们应注意什么?
1.找图形的变化规律时,要充分考虑到平移和旋转的特征。
2.解决下幅图的个数问题时,可以按照规律继续画一画,也可以用算式计算。
复习旧知
1.按规律接着画两个。
巩固练习
通过观察可以看出,三角形是按照顺时针方向依次旋转90°。
2.舞台上有15只小熊参加表演,一共多少条腿着地?
后面的小熊都是两条腿着地。
通过观察可知,第一只小熊4条腿着地,后面的小熊2条腿着地,因此共有:
4+2×(15-1)
=4+2×14
=32(条)
答:共有32条腿着地。
3.找出规律,接着画。
由题意可知:图形在方格中进行顺时针旋转,据此画图即可。
小结5
1.找图形的变化规律时,要充分考虑平移和旋转的特征。
2.解决下幅图的个数问题时,可以按照规律继续画一画,也可以用算式计算。
谢 谢
