苏科版数学七年级册第2章 有理数全章知识点复习知识点复习学案
文档属性
| 名称 | 苏科版数学七年级册第2章 有理数全章知识点复习知识点复习学案 |  | |
| 格式 | zip | ||
| 文件大小 | 218.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-27 15:35:19 | ||
图片预览




文档简介
有理数和无理数
学前引导:
进入初中阶段我们首先引入了正数和负数。所以必须先了解这两个数的概念。
概念:
正数:大于0的数,正数前面用“+”来表示(通常省略不写)。正数可分为正整数和正分数。
负数:小于0的数,负数前面用“-”来表示(不可省略)。负数可分为负整数和负分数。
特别注意:
0既不是正数,也不是负数。但是:0属于偶数、自然数、整数、非正数、非负数、非正整数、非负整数。
总结:
我们把正整数、零和负整数统称为整数,正分数、负分数统称分数。
进入主题:
有理数:
整数和分数统称为有理数。
图文解释:如(图一,图二)
无理数:
无限不循环小数(比如π,)
有理数知识点总结:
(1)有理数可以按照整数,分数分类。也可以按照正有理数,0,负有理数分类。
(2)在分类时,要注意0的地位和意义。
(3)习惯上,把正整数、0统称为非负整数(也叫自然数);把负整数、0统称为非正整数,
无理数知识点总结:
(1)只有满足“无限”和“不循环”这两个条件,才是无理数。
(2)无理数与有理数的和差一定是无理数。
(3)无理数乘或除以一个不为0的有理数一定是无理数.如2π、π
(4)无理数分类比较简单可以分为:正无理数和负无理数。
特别注意分数与无理数的区别:
分数必须先化简再作判断
(分数可以化为有限小数和无线循环小数,这是与无理数的区别。其中百分数也是分数的一种形式)
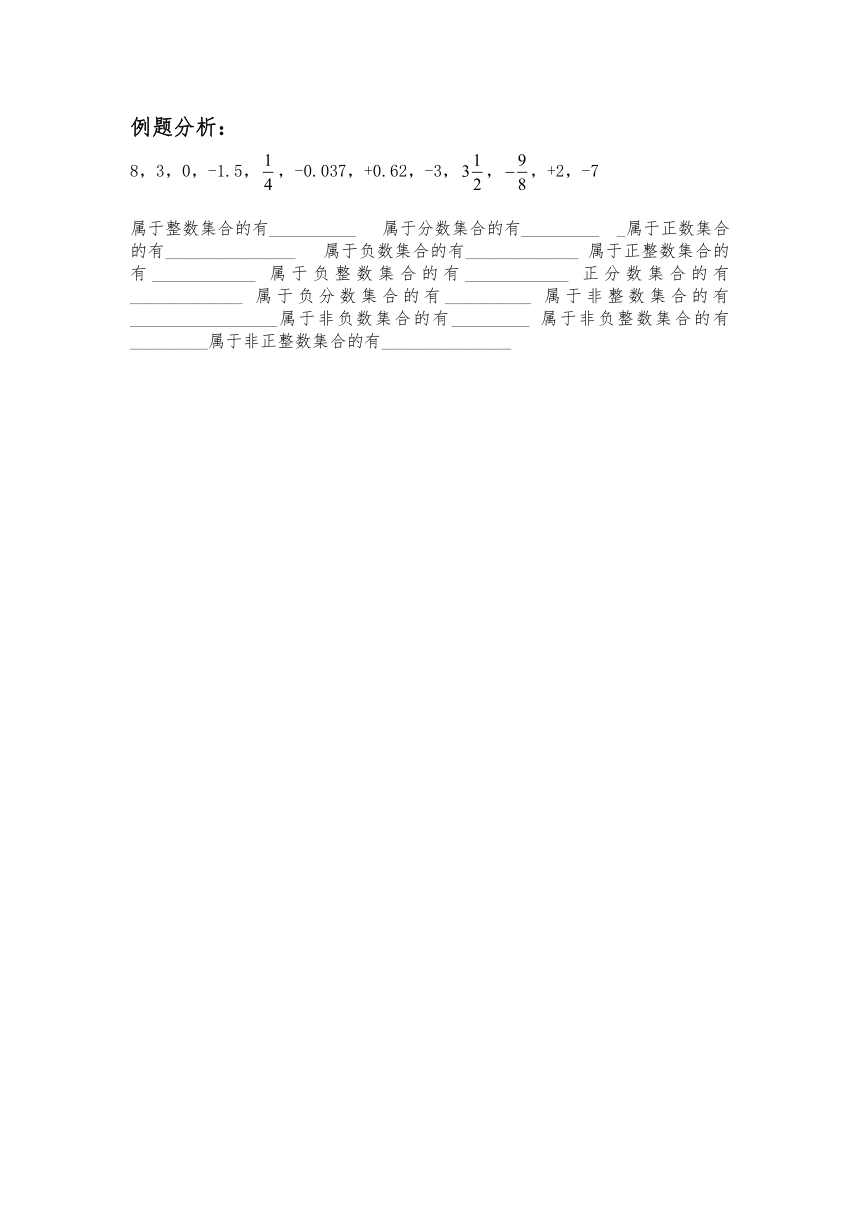
例题分析:
0
-1
+2
-5%
1.2
-
0.1010010001....
0.0101001
Π
-3.1415926
-0.58
80%
+24
-90
6.9
-
正数集合:
负数集合:
非负数集合:
非正数集合:
整数集合:
分数集合:
自然数集合:
有理数集合:
无理数集合:
例题分析:
8,3,0,-1.5,,-0.037,+0.62,-3,,,+2,-7
属于整数集合的有__________
属于分数集合的有_________
_属于正数集合的有_______________
属于负数集合的有_____________
属于正整数集合的有____________
属于负整数集合的有____________
正分数集合的有_____________
属于负分数集合的有__________
属于非整数集合的有_________________属于非负数集合的有_________
属于非负整数集合的有_________属于非正整数集合的有_______________
数轴、绝对值、相反数
数轴:
定义:规定了原点、正方向、单位长度的直线叫作数轴(这也是数轴的三要素)
(注意这里说的规定,意思是可以根据实际情况取数轴的三要素)
为什么要引入数轴
:
1.
可以清楚地区分正数、0、负数
;
2.
有理数和无理数都可以用数轴上的点表示;
3.
反过来,数轴上的任意一点都可以表示一个有理数或无理数。
数轴上点的性质:
在数轴上表示的两个数,右边的数总比左边的数大。
正数都大于0,负数都小于0,正数大于负数。
拓展:
(1)
举例:数轴上A对应的数为-3,B对应数为1,则AB中点对应的数为
数轴上A对应的数为-3,B对应数为-1,则AB中点对应的数为
数轴上A对应的数为3,B对应数为1,则AB中点对应的数为
(2)数轴上任意两点的距离公式:
右边点表示的数-左边点表示的数。
举例:数轴上A对应的数为-3,B对应的数为-2,则线段AB的长为:-2-(-3)=1
数轴上A对应的数为3,B对应的数为-2,则线段AB的长度为:3-(-2)=5
数轴上A对应的数为3,B对应的数为+2,则线段AB的长度为:3-(+2)=1
(3)数轴上运动的点表示的数:
一定要先规定起点对应的数为a
动点向右运动b个单位,则表示的数为:a+b;
动点向左运动b个单位,则表示的数为:a-b;
举例:数轴上A对应的数为2,动点Q从A点向右移动3个单位,此时Q点对应的数为:2+3=5
数轴上A对应的数为2,动点Q从A点向左移动3个单位,此时Q点对应的数为:2-3=-1
数轴上A对应的数为-2,动点Q从A点向右移动3个单位,此时Q点对应的数为:-2+3=1
数轴上A对应的数为-2,动点Q从A点向左移动3个单位,此时Q点对应的数为:-2-3=-5
绝对值:
定义:数轴上的点与原点的距离叫作这个数的绝对值
注意:绝对值表示的是长度
例如:
表示-2的点到原点的距离为2,所以我们说-2的绝对值为2。
表示2的点到原点的距离为2,所以我们说2的绝对值为2。
表示0的点到原点的距离为0,因此0的绝对值为0。
绝对值的表示:
通常,我们将数a的绝对值表示为|a|,例如:-2的绝对值表示为|-2|=2,|2|=2,|0|=0
拓展:
注意:对于|a-b|或|b-a|表示:数轴上数a对应点到数b对应点的距离。注意绝对值里面要要看作一个数减去另外一个数的形式,对于|a+b|,通常改写为|a-(-b)|表示数a对应点到数-b对应点的距离。
举例:|-3-2|表示-3对应点到2对应点的距离为5。
|-3+2|首先改成|-3-(-2)|表示-3对应点到-2对应点的距离为1。
在数轴上点A对应的数是-3,点B对应的数为-2,则AB中点对应的数为:
=-
相反数:
定义:符号不同、绝对值相同的两个数互为相反数,其中一个数叫作另外一个数的相反数。
注意:相反数是相对于两个数而言的。
例如:2与-2互为相反数,其中2是-2的相反数,或者-2是2的相反数。
0的相反数为0。
相反数的表示:
通常表示一个数的相反数,我们可以在这个数前面加和“-”号.例如:5的相反数可以表示为-5,-5的相反数可以表示为-(-5)=5。
绝对值和相反数总结:
绝对值:
正数的绝对值是它本身;
即当a>0时,|a|=a;
负数的绝对值是它的相反数;
即当a<0时,|a|=-a;
0的绝对值是0;
即a=0时,|a|=0;
绝对值比大小:
两个正数,绝对值大的正数大;两个负数,绝对值大的负数小。
相反数:
互为相反数的两个数和为0;
有理数的加法与减法
有理数的加法法则:
同号两数相加:
结果先取相同的符号,再将这两个数的绝对值相加。
异号两数相加:
绝对值相等,结果为0.
绝对值不等,结果先取绝对值较大数的符号,再用较大绝对值减较小绝对值。
注意:
这里说的同号和异号是指两个正数相加或两个负数相加或一个正数和一个负数相加。
先取结果的符号,就是要先确定结果的正负性。
例如:(-15)+(-3)
先明确为两负数相加(也叫同号两数相加),再确定结果肯定为负数,将两数的绝对值相加为18,所以最后结果为-18
(-180)+(+20)先明确为一个正数和一个负数相加(也叫异号两数相加),再确定结果肯定为负数,因为-180的绝对值大,即取“-”号,再用较大绝对值减较小绝对值为160,所以最后结果为-160
(+180)+(-20)先明确为一个正数和一个负数相加(也叫异号两数相加),再确定结果肯定为正数,因为+180的绝对值大,即取“+”号,再用较大绝对值减较小绝对值为160,所以最后结果为+160
有理数的减法法则:
减去一个数等于加上这个数的相反数。
注意:减法必须要转化为加法,然后用加法法则计算。
一定要明确减的是正数还是负数。
例如:(-15)-(+3)表示减的是+3,所以应该加上+3的相反数-3;
即原式可变为(-15)+(-3);
(-15)-(-3)表示减的是-3,所以应该加上-3的相反数+3;
即原式可变为(-15)+(+3);
怎样做好有理数的加法运算:
1、一定要保证每一个加数前面只有一个符号。
举例:
-(-3)
3前面两个负号,可以改成+3,两个负号变正号
+(-3)
3前面一个负号一个正号,可以改成-3,去掉正号。
-(+3)
3前面一个正号一个负号,可以改成-3,去掉正号。
(也就是正号和负号在一起可以直接去掉正号,两负号在一起可以变一个正号)
2、保证每个加数前面只有一个符号后,再明确是哪几个加数相加。
举例:2+5-8,可以看作+2、+5、-8三个数相加,
-14-27+12-17,可以看作-14、-17、+12、-17
四个加数相加。
3、掌握两个加法运算律:
交换律:a+b=b+a
结合律:(a+b)+c=a+(b+c)
总结:
确定每一个数前面的符号很重要。
初中有理数加减法运算,不像小学加减法,因为涉及到负数。
为了适应加法法则,要习惯看成哪几个数相加的形式。
习惯忘记小学中的加号和减号,当确定好每个数前面的符号后,你看到的加号表
示这个数的正号,你看的的减号表示这个数的负号。
交换律和结合律只是告诉你,正数要和正数先加,负数要和负数先加。
(确定每个数前面是正号还是负号尤为重要,如果不确定好,往往开头就错了。无论是以后的有理数混合运算还是幂的运算,)都要注意这点!!!)
有理数的乘除法与乘方
有理数的的乘法法则:
两数相乘同号得正,异号得负,并把绝对值相乘。0与任何数相乘都为0。
注意:这里说的同号指是正数与正数相乘,负数与负数相乘,此时结果为正数
异号是指正数与负数相乘,此时结果为负数。
确定完结果的正负性,再将两数的绝对值相乘得结果。
举例:(-9)×(-6)明确为两负数相乘,即同号相乘,确定结果肯定为正数。
再分别取(-9)和(-6)两数的绝对值相乘为54,最后结果为+54。
(-9)×(+6)明确为负数和正数相乘,即异号相乘,确定结果肯定为负数。再分别取(-9)和(+6)两数的绝对值相乘为54,最后结果为-54。
书写:乘号和正号在一起可以直接省去正号。比如(-9)×(+6)可以写成(-9)×6,乘号和负数在一起负数必须要加括号,比如(-9)×(-6)不能写成(-9)×-6,括号为了将“×”号和“-”号隔开。
有理数的的除法法则:
除以一个不等于0的数,等于乘这个数的倒数。
(有理数除法可以转化为乘法,所以他有与乘法类似的法则。)
两个不为0的数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不为0的数都为0。
注意:遇到除法我们最好转化为乘法,然后运用乘法法则计算。
乘积为1的两个数互为倒数。倒数是相对于两个数而言的。
正数的倒数是正数,负数的倒数是负数(即互为倒数的两个数符号相同)
0没有倒数,因为0与任何数的乘积都不为1。
举例:14÷(-7)可以写成14×(-),然后运用乘法法则计算。
-7÷(-7)可以写成-7×(-)=1.其中-7和-互为倒数,
-7为-的倒数,或者说-为-7的倒数。
怎样做好有理数的乘除法:
1、遇到除法转化为乘法。
2、要确定是哪两个数相乘,所以必须要先确定每一个数前面的符号。
3、一定要先确定结果是正数还是负数,这样就不会因为符号导致结果错误。
4、要掌握乘法运算律。
交换律:a×b=b×a
结合律:(a×b)×c=
a×(b×c)
分配律:a×(b+c)=a×b+a×c
注意:除法没有分配律
(一个数与两个数的和相乘,等于把这个数分别与这两个数相乘,再把积相加)
5、有n个负数相乘,若n为偶数时,积为正数;当n为奇数时,积为负数。
有理数的乘方:
一般的,在数学上我们把n个相同的因数a相乘的积记做an,即:
记作
读作“a的n次方”。
我们把求相同因数的积的运算叫做乘方,相同因数叫作底数,因数的个数叫作指数,运算出来的结果叫做幂。
例如:2×2×2×2×2=2
这时2也可以看作乘方运算的结果,这时候他们表示为数,读作2的5次幂,其中2叫作底数,3叫作指数。
总结:正数的任何次幂都是正数
负数的奇数次幂是负数,负数的偶数次幂是正数。
特别地,一个数的二次方也叫作这个数的平方,一个数的三次方也叫这个数的立方。
科学计数法:
一般地,一个大于10的数可以写成a×10n的形式,其中1≤a<10,n是正整数,这种记数法称为科学计数法。如1800
000=1.8×106
(为什么要科学计数法,使数书写简单)
科学计数法的方法:
1、移小数点法
2、减“1”法
(10的指数位等于整数位减1)
学前引导:
进入初中阶段我们首先引入了正数和负数。所以必须先了解这两个数的概念。
概念:
正数:大于0的数,正数前面用“+”来表示(通常省略不写)。正数可分为正整数和正分数。
负数:小于0的数,负数前面用“-”来表示(不可省略)。负数可分为负整数和负分数。
特别注意:
0既不是正数,也不是负数。但是:0属于偶数、自然数、整数、非正数、非负数、非正整数、非负整数。
总结:
我们把正整数、零和负整数统称为整数,正分数、负分数统称分数。
进入主题:
有理数:
整数和分数统称为有理数。
图文解释:如(图一,图二)
无理数:
无限不循环小数(比如π,)
有理数知识点总结:
(1)有理数可以按照整数,分数分类。也可以按照正有理数,0,负有理数分类。
(2)在分类时,要注意0的地位和意义。
(3)习惯上,把正整数、0统称为非负整数(也叫自然数);把负整数、0统称为非正整数,
无理数知识点总结:
(1)只有满足“无限”和“不循环”这两个条件,才是无理数。
(2)无理数与有理数的和差一定是无理数。
(3)无理数乘或除以一个不为0的有理数一定是无理数.如2π、π
(4)无理数分类比较简单可以分为:正无理数和负无理数。
特别注意分数与无理数的区别:
分数必须先化简再作判断
(分数可以化为有限小数和无线循环小数,这是与无理数的区别。其中百分数也是分数的一种形式)
例题分析:
0
-1
+2
-5%
1.2
-
0.1010010001....
0.0101001
Π
-3.1415926
-0.58
80%
+24
-90
6.9
-
正数集合:
负数集合:
非负数集合:
非正数集合:
整数集合:
分数集合:
自然数集合:
有理数集合:
无理数集合:
例题分析:
8,3,0,-1.5,,-0.037,+0.62,-3,,,+2,-7
属于整数集合的有__________
属于分数集合的有_________
_属于正数集合的有_______________
属于负数集合的有_____________
属于正整数集合的有____________
属于负整数集合的有____________
正分数集合的有_____________
属于负分数集合的有__________
属于非整数集合的有_________________属于非负数集合的有_________
属于非负整数集合的有_________属于非正整数集合的有_______________
数轴、绝对值、相反数
数轴:
定义:规定了原点、正方向、单位长度的直线叫作数轴(这也是数轴的三要素)
(注意这里说的规定,意思是可以根据实际情况取数轴的三要素)
为什么要引入数轴
:
1.
可以清楚地区分正数、0、负数
;
2.
有理数和无理数都可以用数轴上的点表示;
3.
反过来,数轴上的任意一点都可以表示一个有理数或无理数。
数轴上点的性质:
在数轴上表示的两个数,右边的数总比左边的数大。
正数都大于0,负数都小于0,正数大于负数。
拓展:
(1)
举例:数轴上A对应的数为-3,B对应数为1,则AB中点对应的数为
数轴上A对应的数为-3,B对应数为-1,则AB中点对应的数为
数轴上A对应的数为3,B对应数为1,则AB中点对应的数为
(2)数轴上任意两点的距离公式:
右边点表示的数-左边点表示的数。
举例:数轴上A对应的数为-3,B对应的数为-2,则线段AB的长为:-2-(-3)=1
数轴上A对应的数为3,B对应的数为-2,则线段AB的长度为:3-(-2)=5
数轴上A对应的数为3,B对应的数为+2,则线段AB的长度为:3-(+2)=1
(3)数轴上运动的点表示的数:
一定要先规定起点对应的数为a
动点向右运动b个单位,则表示的数为:a+b;
动点向左运动b个单位,则表示的数为:a-b;
举例:数轴上A对应的数为2,动点Q从A点向右移动3个单位,此时Q点对应的数为:2+3=5
数轴上A对应的数为2,动点Q从A点向左移动3个单位,此时Q点对应的数为:2-3=-1
数轴上A对应的数为-2,动点Q从A点向右移动3个单位,此时Q点对应的数为:-2+3=1
数轴上A对应的数为-2,动点Q从A点向左移动3个单位,此时Q点对应的数为:-2-3=-5
绝对值:
定义:数轴上的点与原点的距离叫作这个数的绝对值
注意:绝对值表示的是长度
例如:
表示-2的点到原点的距离为2,所以我们说-2的绝对值为2。
表示2的点到原点的距离为2,所以我们说2的绝对值为2。
表示0的点到原点的距离为0,因此0的绝对值为0。
绝对值的表示:
通常,我们将数a的绝对值表示为|a|,例如:-2的绝对值表示为|-2|=2,|2|=2,|0|=0
拓展:
注意:对于|a-b|或|b-a|表示:数轴上数a对应点到数b对应点的距离。注意绝对值里面要要看作一个数减去另外一个数的形式,对于|a+b|,通常改写为|a-(-b)|表示数a对应点到数-b对应点的距离。
举例:|-3-2|表示-3对应点到2对应点的距离为5。
|-3+2|首先改成|-3-(-2)|表示-3对应点到-2对应点的距离为1。
在数轴上点A对应的数是-3,点B对应的数为-2,则AB中点对应的数为:
=-
相反数:
定义:符号不同、绝对值相同的两个数互为相反数,其中一个数叫作另外一个数的相反数。
注意:相反数是相对于两个数而言的。
例如:2与-2互为相反数,其中2是-2的相反数,或者-2是2的相反数。
0的相反数为0。
相反数的表示:
通常表示一个数的相反数,我们可以在这个数前面加和“-”号.例如:5的相反数可以表示为-5,-5的相反数可以表示为-(-5)=5。
绝对值和相反数总结:
绝对值:
正数的绝对值是它本身;
即当a>0时,|a|=a;
负数的绝对值是它的相反数;
即当a<0时,|a|=-a;
0的绝对值是0;
即a=0时,|a|=0;
绝对值比大小:
两个正数,绝对值大的正数大;两个负数,绝对值大的负数小。
相反数:
互为相反数的两个数和为0;
有理数的加法与减法
有理数的加法法则:
同号两数相加:
结果先取相同的符号,再将这两个数的绝对值相加。
异号两数相加:
绝对值相等,结果为0.
绝对值不等,结果先取绝对值较大数的符号,再用较大绝对值减较小绝对值。
注意:
这里说的同号和异号是指两个正数相加或两个负数相加或一个正数和一个负数相加。
先取结果的符号,就是要先确定结果的正负性。
例如:(-15)+(-3)
先明确为两负数相加(也叫同号两数相加),再确定结果肯定为负数,将两数的绝对值相加为18,所以最后结果为-18
(-180)+(+20)先明确为一个正数和一个负数相加(也叫异号两数相加),再确定结果肯定为负数,因为-180的绝对值大,即取“-”号,再用较大绝对值减较小绝对值为160,所以最后结果为-160
(+180)+(-20)先明确为一个正数和一个负数相加(也叫异号两数相加),再确定结果肯定为正数,因为+180的绝对值大,即取“+”号,再用较大绝对值减较小绝对值为160,所以最后结果为+160
有理数的减法法则:
减去一个数等于加上这个数的相反数。
注意:减法必须要转化为加法,然后用加法法则计算。
一定要明确减的是正数还是负数。
例如:(-15)-(+3)表示减的是+3,所以应该加上+3的相反数-3;
即原式可变为(-15)+(-3);
(-15)-(-3)表示减的是-3,所以应该加上-3的相反数+3;
即原式可变为(-15)+(+3);
怎样做好有理数的加法运算:
1、一定要保证每一个加数前面只有一个符号。
举例:
-(-3)
3前面两个负号,可以改成+3,两个负号变正号
+(-3)
3前面一个负号一个正号,可以改成-3,去掉正号。
-(+3)
3前面一个正号一个负号,可以改成-3,去掉正号。
(也就是正号和负号在一起可以直接去掉正号,两负号在一起可以变一个正号)
2、保证每个加数前面只有一个符号后,再明确是哪几个加数相加。
举例:2+5-8,可以看作+2、+5、-8三个数相加,
-14-27+12-17,可以看作-14、-17、+12、-17
四个加数相加。
3、掌握两个加法运算律:
交换律:a+b=b+a
结合律:(a+b)+c=a+(b+c)
总结:
确定每一个数前面的符号很重要。
初中有理数加减法运算,不像小学加减法,因为涉及到负数。
为了适应加法法则,要习惯看成哪几个数相加的形式。
习惯忘记小学中的加号和减号,当确定好每个数前面的符号后,你看到的加号表
示这个数的正号,你看的的减号表示这个数的负号。
交换律和结合律只是告诉你,正数要和正数先加,负数要和负数先加。
(确定每个数前面是正号还是负号尤为重要,如果不确定好,往往开头就错了。无论是以后的有理数混合运算还是幂的运算,)都要注意这点!!!)
有理数的乘除法与乘方
有理数的的乘法法则:
两数相乘同号得正,异号得负,并把绝对值相乘。0与任何数相乘都为0。
注意:这里说的同号指是正数与正数相乘,负数与负数相乘,此时结果为正数
异号是指正数与负数相乘,此时结果为负数。
确定完结果的正负性,再将两数的绝对值相乘得结果。
举例:(-9)×(-6)明确为两负数相乘,即同号相乘,确定结果肯定为正数。
再分别取(-9)和(-6)两数的绝对值相乘为54,最后结果为+54。
(-9)×(+6)明确为负数和正数相乘,即异号相乘,确定结果肯定为负数。再分别取(-9)和(+6)两数的绝对值相乘为54,最后结果为-54。
书写:乘号和正号在一起可以直接省去正号。比如(-9)×(+6)可以写成(-9)×6,乘号和负数在一起负数必须要加括号,比如(-9)×(-6)不能写成(-9)×-6,括号为了将“×”号和“-”号隔开。
有理数的的除法法则:
除以一个不等于0的数,等于乘这个数的倒数。
(有理数除法可以转化为乘法,所以他有与乘法类似的法则。)
两个不为0的数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不为0的数都为0。
注意:遇到除法我们最好转化为乘法,然后运用乘法法则计算。
乘积为1的两个数互为倒数。倒数是相对于两个数而言的。
正数的倒数是正数,负数的倒数是负数(即互为倒数的两个数符号相同)
0没有倒数,因为0与任何数的乘积都不为1。
举例:14÷(-7)可以写成14×(-),然后运用乘法法则计算。
-7÷(-7)可以写成-7×(-)=1.其中-7和-互为倒数,
-7为-的倒数,或者说-为-7的倒数。
怎样做好有理数的乘除法:
1、遇到除法转化为乘法。
2、要确定是哪两个数相乘,所以必须要先确定每一个数前面的符号。
3、一定要先确定结果是正数还是负数,这样就不会因为符号导致结果错误。
4、要掌握乘法运算律。
交换律:a×b=b×a
结合律:(a×b)×c=
a×(b×c)
分配律:a×(b+c)=a×b+a×c
注意:除法没有分配律
(一个数与两个数的和相乘,等于把这个数分别与这两个数相乘,再把积相加)
5、有n个负数相乘,若n为偶数时,积为正数;当n为奇数时,积为负数。
有理数的乘方:
一般的,在数学上我们把n个相同的因数a相乘的积记做an,即:
记作
读作“a的n次方”。
我们把求相同因数的积的运算叫做乘方,相同因数叫作底数,因数的个数叫作指数,运算出来的结果叫做幂。
例如:2×2×2×2×2=2
这时2也可以看作乘方运算的结果,这时候他们表示为数,读作2的5次幂,其中2叫作底数,3叫作指数。
总结:正数的任何次幂都是正数
负数的奇数次幂是负数,负数的偶数次幂是正数。
特别地,一个数的二次方也叫作这个数的平方,一个数的三次方也叫这个数的立方。
科学计数法:
一般地,一个大于10的数可以写成a×10n的形式,其中1≤a<10,n是正整数,这种记数法称为科学计数法。如1800
000=1.8×106
(为什么要科学计数法,使数书写简单)
科学计数法的方法:
1、移小数点法
2、减“1”法
(10的指数位等于整数位减1)
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
