勾股定理(第一课时)
图片预览
文档简介
勾股定理(第一课时)
学习目标:1. 勾股定理的内容.
2. 如何验证勾股定理的内容.
3. 利用勾股定理,已知直角三角形的两边求第三边的长.
一.自主学习
(一)温故知新
1.直角三角形的性质:(1)直角三角形两锐角 ;
(2)直角三角形斜边上的中线等于 ;
(3)直角三角形中30°的角所对的直角边等于 。
2.分别求出下式中的x的值:① x2=5 ② (x-2)2=5 ③ 4(2x-1)2=9
二. 合作交流
1. 完成P65的探究,猜想得出的结论: 。
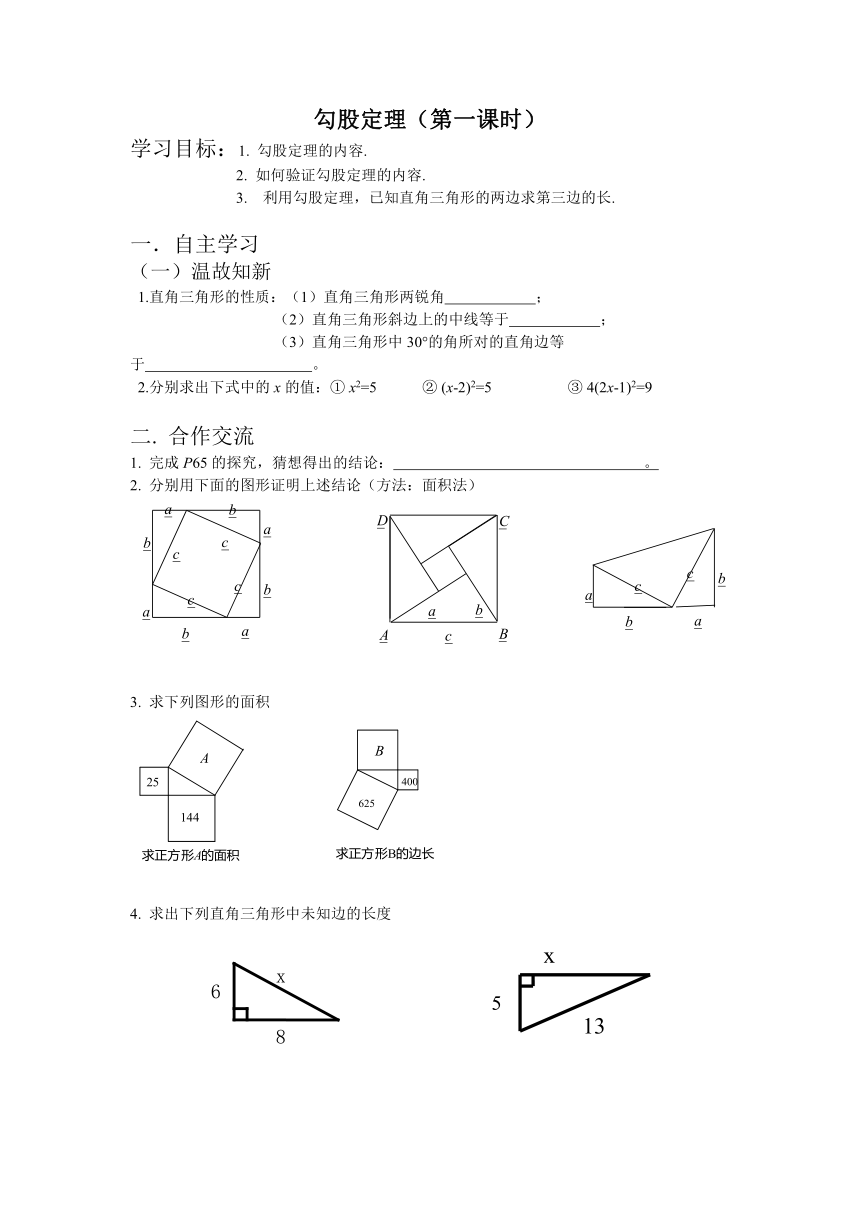
2. 分别用下面的图形证明上述结论(方法:面积法)
3. 求下列图形的面积
4. 求出下列直角三角形中未知边的长度
三. 展示升华
完成“合作交流”中的四个问题,并进行学生展示,教师点评.
四.达标巩固
1.在Rt△ABC中, ∠C=90°,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b;
(4) 若a : b = 1:2 ,c=6,则a,b各多长
(5)若∠A=300,a=3,则b , c各多长
五.课时训练
基础过关:
1.在Rt△ABC中,∠C=90°
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC =________。
2.已知在Rt△ABC中,∠B=90°,a、b、c是△ABC的三边,则
⑴c= 。(已知a、b,求c)
⑵a= 。(已知b、c,求a)
⑶b= 。(已知a、c,求b)
强化提升
1.在一个直角三角形中,若斜边的长是,一条直角边的长为,那么这个
直角三角形的面积是( )
(A) (B) (C) (D)
2. 在直角三角形ABC中,斜边AB=1,则AB的值是( )
A.2 B.4 C.6 D.8
3. 已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A、25 B、14 C、7 D、7或25
4. 如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯多少米?
5. 直角三角形两直角边长分别为5和12,则它斜边上的高为__________。
6.. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们
仅仅少走了 步路(假设2步为1米),却踩伤了花草.
7. (2008年株洲市)如图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是 米.
8. 等腰三角形底边上的高为8,周长为32,求这个三角形的面积的值。
9. 一个零件的形状如图所示,已知AC=3,AB=4,BD=12
求CD的长.
10. 如图所示,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,
求AB的长.
_
a
_
b
_
c
_
a
_
c
_
b
_
a
_
a
_
b
_
c
_
b
_
c
_
a
_
b
_
c
_
c
_
b
_
a
_
a
_
c
_
b
_
D
_
C
_
B
_
A
x
x
6
8
13
5
第4题
第6题
第7题
第9题图
第10题图
学习目标:1. 勾股定理的内容.
2. 如何验证勾股定理的内容.
3. 利用勾股定理,已知直角三角形的两边求第三边的长.
一.自主学习
(一)温故知新
1.直角三角形的性质:(1)直角三角形两锐角 ;
(2)直角三角形斜边上的中线等于 ;
(3)直角三角形中30°的角所对的直角边等于 。
2.分别求出下式中的x的值:① x2=5 ② (x-2)2=5 ③ 4(2x-1)2=9
二. 合作交流
1. 完成P65的探究,猜想得出的结论: 。
2. 分别用下面的图形证明上述结论(方法:面积法)
3. 求下列图形的面积
4. 求出下列直角三角形中未知边的长度
三. 展示升华
完成“合作交流”中的四个问题,并进行学生展示,教师点评.
四.达标巩固
1.在Rt△ABC中, ∠C=90°,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b;
(4) 若a : b = 1:2 ,c=6,则a,b各多长
(5)若∠A=300,a=3,则b , c各多长
五.课时训练
基础过关:
1.在Rt△ABC中,∠C=90°
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC =________。
2.已知在Rt△ABC中,∠B=90°,a、b、c是△ABC的三边,则
⑴c= 。(已知a、b,求c)
⑵a= 。(已知b、c,求a)
⑶b= 。(已知a、c,求b)
强化提升
1.在一个直角三角形中,若斜边的长是,一条直角边的长为,那么这个
直角三角形的面积是( )
(A) (B) (C) (D)
2. 在直角三角形ABC中,斜边AB=1,则AB的值是( )
A.2 B.4 C.6 D.8
3. 已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A、25 B、14 C、7 D、7或25
4. 如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯多少米?
5. 直角三角形两直角边长分别为5和12,则它斜边上的高为__________。
6.. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们
仅仅少走了 步路(假设2步为1米),却踩伤了花草.
7. (2008年株洲市)如图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是 米.
8. 等腰三角形底边上的高为8,周长为32,求这个三角形的面积的值。
9. 一个零件的形状如图所示,已知AC=3,AB=4,BD=12
求CD的长.
10. 如图所示,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,
求AB的长.
_
a
_
b
_
c
_
a
_
c
_
b
_
a
_
a
_
b
_
c
_
b
_
c
_
a
_
b
_
c
_
c
_
b
_
a
_
a
_
c
_
b
_
D
_
C
_
B
_
A
x
x
6
8
13
5
第4题
第6题
第7题
第9题图
第10题图
