四边形复习

(共20张PPT)
主讲：宋文慧
2007年4月
设计制作：宋文慧
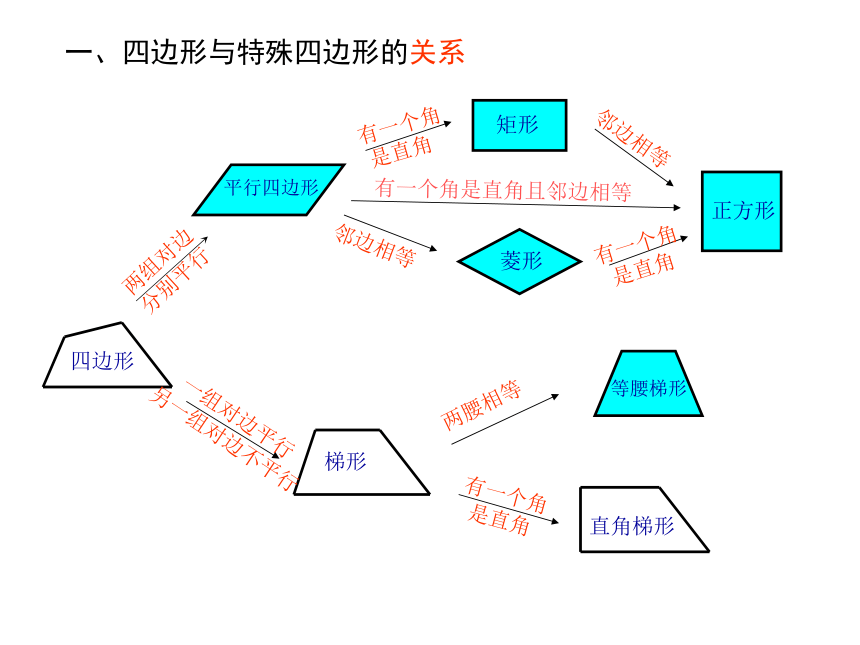
一、四边形与特殊四边形的关系
四边形
平行四边形
矩形
菱形
正方形
梯形
等腰梯形
直角梯形
两组对边
分别平行
有一个角
是直角
邻边相等
邻边相等
有一个角
是直角
一组对边平行
另一组对边不平行
两腰相等
有一个角
是直角
有一个角是直角且邻边相等
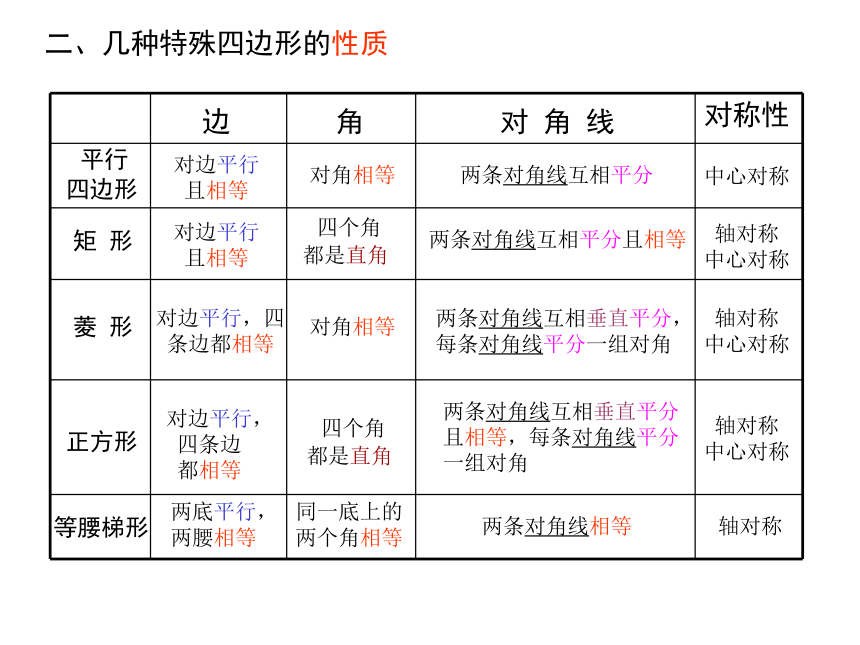
二、几种特殊四边形的性质
平行
四边形
矩 形
菱 形
正方形
等腰梯形
边
对边平行
且相等
对边平行
且相等
对边平行，四
条边都相等
对边平行，
四条边
都相等
两底平行，
两腰相等
角
对角相等
四个角
都是直角
对角相等
四个角
都是直角
同一底上的
两个角相等
对 角 线
两条对角线互相平分
两条对角线互相平分且相等
两条对角线互相垂直平分，
每条对角线平分一组对角
两条对角线互相垂直平分
且相等，每条对角线平分
一组对角
两条对角线相等
对称性
中心对称
轴对称
中心对称
轴对称
中心对称
轴对称
中心对称
轴对称
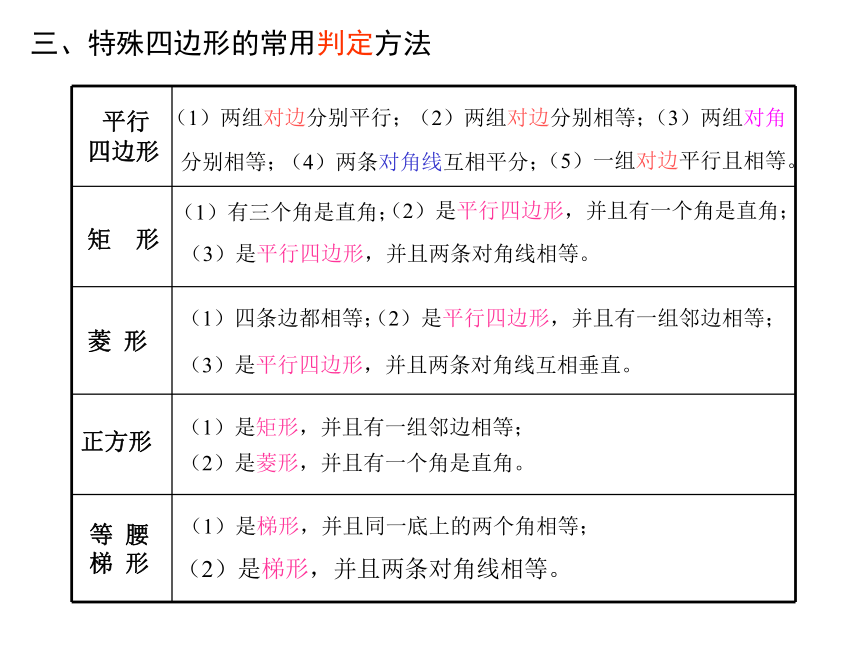
三、特殊四边形的常用判定方法
平行
四边形
（1）两组对边分别平行；
（2）两组对边分别相等；
（5）一组对边
平行且相等。
（4）两条对角线互相平分；
（3）两组对角
矩 形
（1）有三个角是直角；
（2）是平行四边形，并且有一个角是直角；
（3）是平行四边形，并且两条对角线相等。
菱 形
（1）四条边都相等；
（2）是平行四边形，并且有一组邻边相等；
（3）是平行四边形，并且两条对角线互相垂直。
正方形
（1）是矩形，并且有一组邻边相等；
（2）是菱形，并且有一个角是直角。
等 腰
梯 形
（1）是梯形，并且同一底上的两个角相等；
（2）是梯形，并且两条对角线相等。
分别相等；
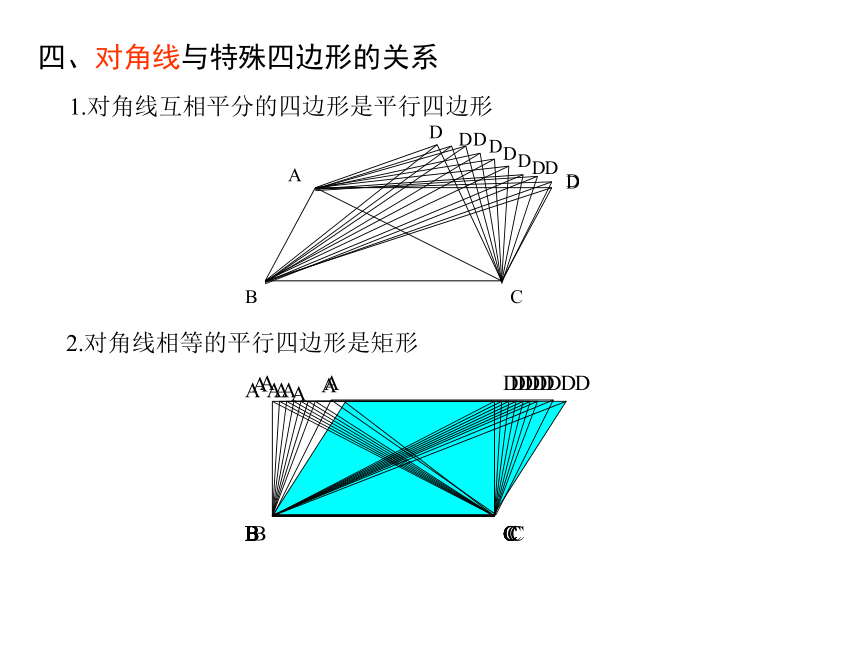
1.对角线互相平分的四边形是平行四边形
2.对角线相等的平行四边形是矩形
A
B
C
D
A
D
B
C
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
四、对角线与特殊四边形的关系
A
B
C
D
D
D
D
D
D
D
D
D
D
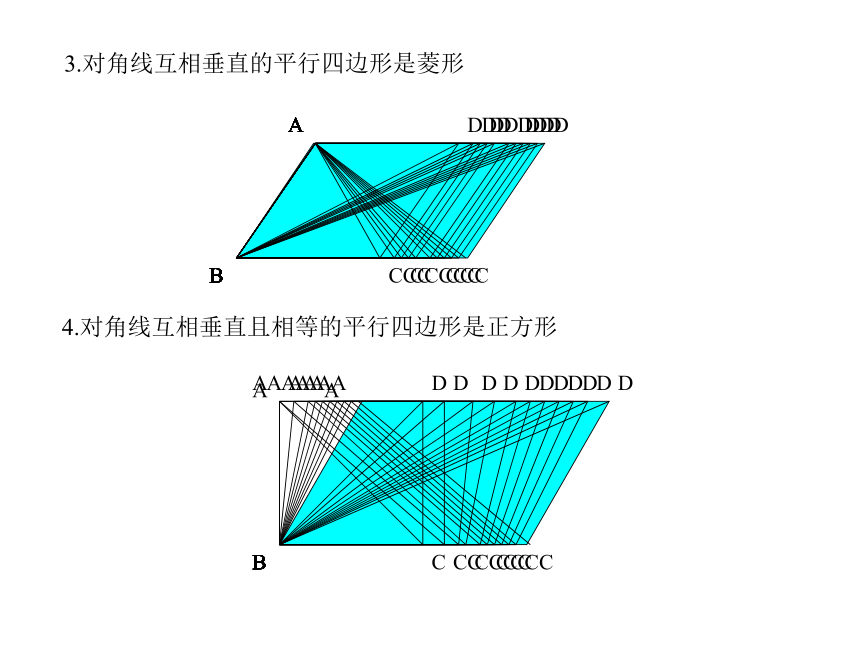
3.对角线互相垂直的平行四边形是菱形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
A
B
C
4.对角线互相垂直且相等的平行四边形是正方形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
C
A
B
D
五、其他重要定理
1. 四边形的内角和等于
360°.
2. n 边形的内角和等于
( n – 2 )
.
180°.
3. 任意多边形的外角和等于
360°.
4. 关于中心对称的两个图形的性质：
（1）是全等形；
（2）对称点的连线都经过对称中心并且被对称中心平分。
六、平行线等分线段定理
如果一组平行线在一条直线上截得的线段相等，那么在其他
直线上截得的线段也相等。
七、三角形、梯形中位线定理
1. 三角形的中位线定理：
A
B
C
D
E
如图，三角形ABC中，AD=DB，AE=EC，
则有 ； 。
DE // BC
DE = BC
1
2
2. 梯形的中位线定理：
A
B
C
D
E
F
如图，梯形ABCD中，AD//BC，EF是中位线，
则有（1） ；
（2） 。
EF// AD// BC
EF = (AD+BC)
1
2
A
B
.
E
.
F
.
G
C
D
P
八、巩固练习
（一）判断题：
1.平行四边形的对角线相等； （ ）
2.矩形的四个角都相等； （ ）
3.菱形的对角线互相垂直平分； （ ）
4.有一个角是直角且邻边相等的平行四边形是正方形； （ ）
5.一组对边平行的四边形是梯形； （ ）
6.有两个角相等的梯形是等腰梯形； （ ）
7.一组对边平行且相等的四边形是平行四边形； （ ）
8.对角线相等的四边形是矩形； （ ）
9.在梯形中上面的底叫做上底，下面的底叫做下底；（ ）
10.正方形既是轴对称图形又是中心对称图形。（ ）
（二）选择题：
(A)一组对边平行，另一组对边也平行；(B)一组对角相等，另一组对角也相等；
1.下面判定四边形是平行四边形的方法中，错误的是（ ）。
(C )一组对边平行，一组对角相等； (D)一组对边平行，另一组对边相等
D
2.正方形具有而菱形不一定具有的性质是（ ）。
(A)对角线互相平分。 (B)对角线相等。
（C）对角线平分一组对角。 (D)对角线互相垂直。
B
3.顺次连结四边形各边中点所得到的四边形一定是（ ）
(A)矩形。 (B)正方形。(C ) 菱形。(D)平行四边形
D
4.内角和等于外角和的多边形是（ ）
(A) 三角形。(B)四边形。(C )五边形。(D)六边形。
B
5.下列性质中，平行四边形不一定具备的是（ ）
(A)对角相等。(B)邻角互补。(C )对角互补。(D)内角和是360°。
C
6.能够判定一个四边形是平行四边形的条件是（ ）
(A)一组对角相等。 (B)两条对角线互相平分。
(C )两条对角线互相垂直。 (D)一对邻角的和为180°。
B
7.下列图形中，既是轴对称图形又是中心对称图形的是（ ）
(A)等边三角形。(B)平行四边形。(C )菱形。(D)等腰梯形。
C
D
9.不能判定四边形ABCD是平行四边形的条件是（ ）
//
(A) AB =CD, AD =BC。(B) BC AD。
(C ) AB//DC, AD//BC。 (D) AB =CD，AD//BC。
D
8.下列图形中，既是轴对称图形又是中心对称图形的是（ ）
(A)
(B)
(C )
(D)
（三）填空题：
相 等
2.两条对角线 的四边形是矩形。
互相平分且相等
3.两条对角线 的平行四边形是菱形。
互 相 垂 直
4.两条对角线 的四边形是菱形。
互相垂直平分
5.两条对角线 的矩形是正方形。
互 相 垂 直
6.两条对角线 的菱形是正方形。
相 等
7.两条对角线 的平行四边形是正方形。
互相垂直并相等
8.两条对角线 的四边形是正方形。
互相垂直平分并相等
9.一个多边形的每一个外角都等于40° ，这个多边形的边数是 ，
它的内角和是 。
9
1260°
10.等腰梯形在同一底上的两个角 ，对角线 。
相 等
相 等
1.两条对角线 的平行四边形是矩形。
11.如图(1)， ABCD中，∠1 = ∠B =50°,则∠2 = 。
A
B
C
D
1
2
(1)
80°
8㎝
12.如图（2），菱形有一个内角是120°，有一条对角线长是8㎝，
A
B
C
D
O
(2)
那么菱形边长是 。
13.已知：正方形的边长是4㎝，则它的对角线的长是 ，
面积是 。
4√2
16
2
㎝
㎝
14.已知，正方形的对角线的长是6 ㎝，则它的边长是 ，
面积是 。
3√2 ㎝
18 ㎝
2
15.已知：正方形的面积是12 ㎝ ，则它的边长是 ，
对角线的长是 。
2
2√3 ㎝
2√6 ㎝
或
3
8
√3 ㎝
九、几种常见的平行四边形辅助线的画法：
1.对角线
A
B
C
D
2.构建新的平行四边形
A
B
C
D
A
B
C
D
E
A
B
C
D
E
3.构建全等三角形
A
B
C
D
E
F
A
B
C
D
E
F
4.构建等腰三角形
A
B
C
D
E
A
B
C
D
E
十、几种常见的梯形的辅助线画法：
1.构建平行四边形
A
B
C
D
F
A
B
C
D
F
2.平移一条对角线
A
B
C
D
E
A
B
C
D
E
3.构建全等三角形
A
B
C
D
E
.
F
A
B
C
D
F
4.构建矩形
A
B
C
D
F
A
B
C
D
E
F
E
E
.
5.作梯形的中位线
A
B
C
D
E
F
6.构建大平行四边形
7.构建三角形
A
B
C
D
E
E
F
C
A
B
D
O
十一、作业： P 195 1、2 （ 做在书上）
P196 3、4、5.
两组对边
分别平行
有一个角
是直角
邻边相等
邻边相等
有一个角
是直角
一组对边平行
另一组对边不平行
两腰相等
有一个角
是直角
四边形
平行四边形
矩形
菱形
正方形
梯形
等腰梯形
直角梯形
有一个角是直角且邻边相等