17.1勾股定理 课件(共24张PPT)
图片预览





文档简介
(共24张PPT)
17.1勾股定理
人教版
八年级
一、教学目标
1、了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2、培养在实际生活中发现问题总结规律的意识和能力。
3、介绍古人在勾股定理研究方面所取得的成就,激发学生的学习热情。
二、重点、难点
重点:勾股定理的内容及其证明。
难点:掌握勾股定理的证明。
情景导入
相传两千五百年前,一次毕达哥拉斯去朋友家做客,发现朋友家的地面图案反映了直角三角形三边的某种数量关系.那么我们也一起来观察下地面,看看能否发现什么数量关系。
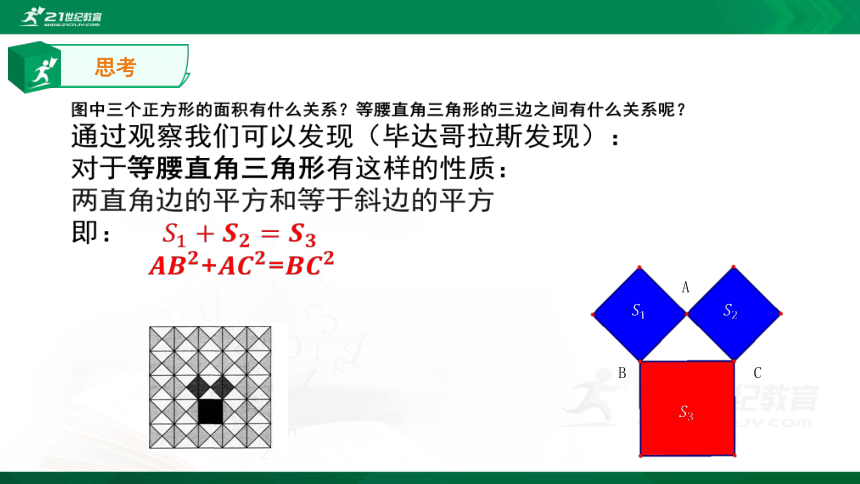
思考
图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系呢?
通过观察我们可以发现(毕达哥拉斯发现):
对于等腰直角三角形有这样的性质:
两直角边的平方和等于斜边的平方
即:
+=
B
A
C
发现
以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积。即等腰直角三角形的三边之间有一种特殊的的关系:斜边的平方等于两直角边的平方和。
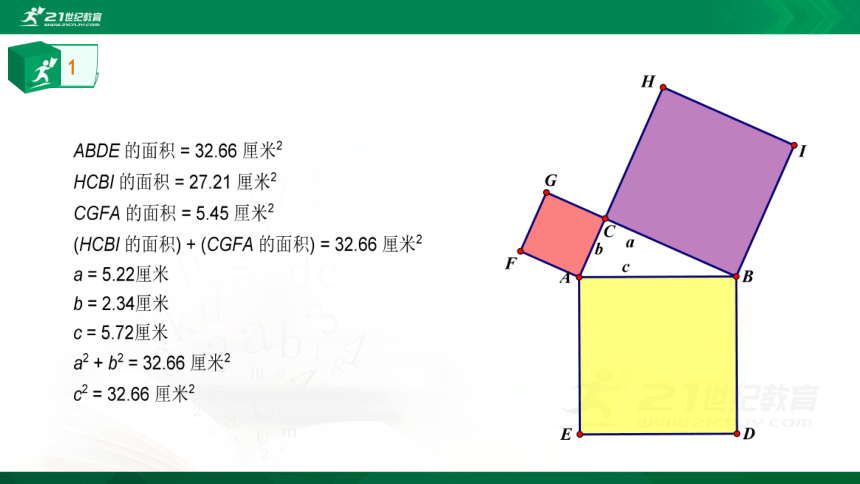
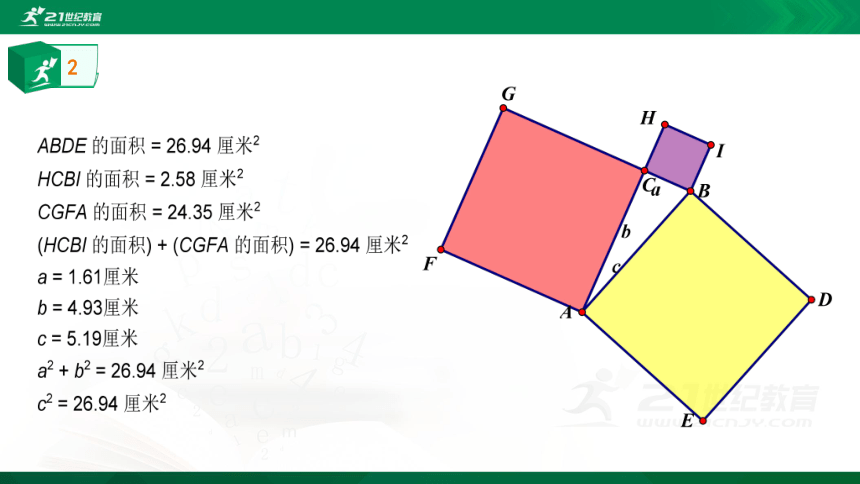
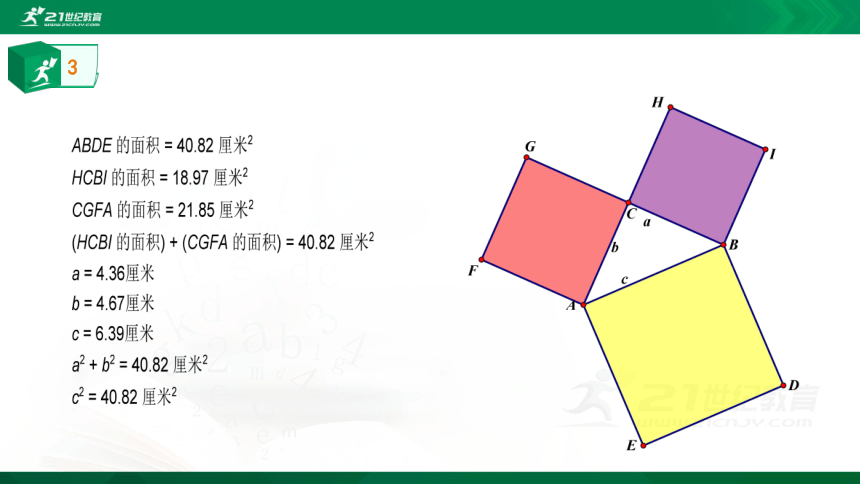
探究
对于
一般的直角三角形
是否也是有上述性质呢?
在下面让我们一起探索一般直角三角形三边之间的数量关系.
请观察下列三种由几何画板绘画出的图形以及相关数量,可得到什么结论呢?
1
2
3
勾股定理
由前面的观察和探究,我们不难发现:
如果直角三角形的两直角边长分别为
??a、b??
,斜边长为
?
c,那么:
b
A
C
c
B
a
=
我们称之为勾股定理(毕达哥拉斯定理).
我国古人对勾股定理的钻研
勾三股四弦五
赵爽弦图——证明了勾股定理
西周《周髀算经》???商高
汉代《周髀算经》注解??
赵爽
勾股定理的证明(赵爽弦图)
由以上的弦图变换可证明勾股定理
得出:
S=
=
欧几里得证明
∵
AF
=
AC,
AB
=
AD,
∠
FAB
=
∠
GAD
,
∴
ΔFAB
≌
ΔGAD
,
∵
ΔFAB
的面积等于
,ΔGAD
的面积等于矩形
ADLM的面积的一半,
∴
矩形
ADLM
的面积
等于
同理可证,矩形
MLEB
的面积等于
∵
正方形
ADEB
的面积
=
矩形
ADLM
的面积
+
矩形MLEB的面积
∴
做三个边长分别为
a
、
b
、
c
的正方形,把它们拼成如图所示形状,使
H
、
C
、
B
三点在一条直线
上,连结
BF
、
CD.
过
C
作
CL
⊥
DE
,交
AB
于点
M
,交
DE
于点
L.
邹元治法
D
G
C
F
B
E
A
H
a
b
a
b
a
b
a
b
c
c
c
c
∵?RtΔHAE?≌?RtΔEBF,?∴?∠AHE?=?∠BEF.?
∵?∠AEH?+?∠AHE?=?90?,∴?∠AEH?+?∠BEF?=?90?.∴?∠HEF?=?180?―90?=?90?.?
∴?四边形EFGH是一个边长为c的正方形.?它的面积等于
∵?RtΔGDH?≌?RtΔHAE,?∴?∠HGD?=?∠EHA.?
∵?∠HGD?+?∠GHD?=?90?,∴?∠EHA?+?∠GHD?=?90?.?
又∵?∠GHE?=?90?,∴?∠DHA?=?90?+?90?=?180?.?
∴?ABCD是一个边长为a?+?b的正方形,它的面积等于∴??∴
做三个边长分别为
a
、
b
、
c
的正方形,把它们拼成如图所示形状,使
H
、
C
、
B
三点在一条直线
上,连结
BF
、
CD.
过
C
作
CL
⊥
DE
,交
AB
于点
M
,交
DE
于点
L.
典例分析
如图,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5m,梯子滑动后停在DE的位置上,如图2,测得BD长为0.5m,求梯子顶端A下落了多少米.
解法指导:
直角三角形中,已知一直角边和斜边是勾股定理的重要应用之一.勾股定理:的各种变式:.应牢固掌握,灵活应用.
分析:先利用勾股定理求出AC与CE的长则梯子顶端A下落的距离为AE=AC-CF.
解:在Rt△ABC中,
?
∴,∴AC=2(m).
?
在Rt△EDC中,,
∴
∴=2.25,∴CE=1.5(m),
?
∴AE=AC-CE=2-1.5=0.5(m)
?
答:梯子顶端A下落了0.5m.
A
C
E
D
B
如图,已知△ABC中,AD为高,且AB+CD=AC+BD,求证:AB=AC.
证明:∵三角形ABD和ACD是直角三角形,
∴AB2-BD2=AC2-CD2
①
又由AB+CD=AC+BD得:
AB-BD=AC-CD
②
由①②得:
AB+BD=AC+CD
③
联立公式②③得:
AB=AC.
A
C
D
B
例1
证明
∵四边形ABCD与四边形EFGH是正方形,
∴∠A=∠D=∠FEH=90°,EF=EH,
∴∠AEF+∠DEH=90°,∠AEF+∠AFE=90°,
∴∠DEH=∠AFE,
在△AEF和△DHE中,
EH=EF,
∠EAF=∠DAE
,∠DEH=∠AFE
∴△AEF≌△DHE,
∴AF=DE=b,
∵DE+AE=1,
∴a+b=1①,
∵SEFGH=EF2=AE2+AF2=
∴ab=
|b—a|=
故答案
D
H
C
G
B
F
A
E
已知:正方形ABCD的边长为1,正方形EFGH内接于ABCD,AE=
a,AF=b,且SEFGH=,则|b-a|的值。
例2
在三角形ABC中,∠A=90,M是BC中点,E.F分别在AC,AB上,且ME⊥MF,探索EF与BF,CE的等量关系,说明理由
例3
结论
证明:
延长EM至N使MN=EM连接BN,FN
∵BM=CM
∠EMC=∠BMN
∴△EMC全等于△BMN
∴∠MEC=∠MEB
∠ECM=∠MBN
EC=BN
∵∠ABC+∠ECM=90°
∴∠ABC+∠MBN=∠FBN=90°
∴
∵FM⊥EM
EM=MN
∴FN=EF
∴
课堂小结
1、了解勾股定理的发现以及其证明过程。
2、通过不同的证明法来掌握勾股定理的证明。
3、学会用面积法证明勾股定理。
4、勾股定理的应用。
随堂测验
1、已知直角三角形两边的长为3和4,则此三角形的周长为__________.
2、某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要????????
__________元.
?3、如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m.同时梯子的顶端B下降至B′,那么BB′(???
).
A.小于1m??
B.大于1m??
C.等于1m?
D.小于或等于1m
?4、将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为h
cm,则h的取值范围是(?
)
A.h≤17cm???
B.h≥8cm?
C.15cm≤h≤16cm?????
D.7cm≤h≤16cm
12或7
150a
A
D
拓展提高
1.
小明想测量教学楼的高度.他用一根绳子从楼顶垂下,发现绳子垂到地面后还多了2
m,当他把绳子的下端拉开6
m后,发现绳子下端刚好接触地面,则教学楼的高为(?????
).?
?
A.
8
m????
B.
10
m????
C.
12
m????
D.
14
m?
2.如果梯子的底端离建筑物9
m,那么15
m长的梯子可以到达建筑物的高度是(?????
).?
A.
10
m???
B.
11
m????
C.
12
m????
D.
13
m?
3.
直角三角形三边的长分别为3、4、x,则x可能取的值有(?????
).?
?
A.
1个????
B.
2
个????
C.
3个?????
D.
无数多个
4、直角三角形中,以直角边为边长的两个正方形的面积为7cm2,8
cm2,则以斜边为边长的正方形的面积为_________
cm2.
A
.C
B?
15
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
17.1勾股定理
人教版
八年级
一、教学目标
1、了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2、培养在实际生活中发现问题总结规律的意识和能力。
3、介绍古人在勾股定理研究方面所取得的成就,激发学生的学习热情。
二、重点、难点
重点:勾股定理的内容及其证明。
难点:掌握勾股定理的证明。
情景导入
相传两千五百年前,一次毕达哥拉斯去朋友家做客,发现朋友家的地面图案反映了直角三角形三边的某种数量关系.那么我们也一起来观察下地面,看看能否发现什么数量关系。
思考
图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系呢?
通过观察我们可以发现(毕达哥拉斯发现):
对于等腰直角三角形有这样的性质:
两直角边的平方和等于斜边的平方
即:
+=
B
A
C
发现
以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积。即等腰直角三角形的三边之间有一种特殊的的关系:斜边的平方等于两直角边的平方和。
探究
对于
一般的直角三角形
是否也是有上述性质呢?
在下面让我们一起探索一般直角三角形三边之间的数量关系.
请观察下列三种由几何画板绘画出的图形以及相关数量,可得到什么结论呢?
1
2
3
勾股定理
由前面的观察和探究,我们不难发现:
如果直角三角形的两直角边长分别为
??a、b??
,斜边长为
?
c,那么:
b
A
C
c
B
a
=
我们称之为勾股定理(毕达哥拉斯定理).
我国古人对勾股定理的钻研
勾三股四弦五
赵爽弦图——证明了勾股定理
西周《周髀算经》???商高
汉代《周髀算经》注解??
赵爽
勾股定理的证明(赵爽弦图)
由以上的弦图变换可证明勾股定理
得出:
S=
=
欧几里得证明
∵
AF
=
AC,
AB
=
AD,
∠
FAB
=
∠
GAD
,
∴
ΔFAB
≌
ΔGAD
,
∵
ΔFAB
的面积等于
,ΔGAD
的面积等于矩形
ADLM的面积的一半,
∴
矩形
ADLM
的面积
等于
同理可证,矩形
MLEB
的面积等于
∵
正方形
ADEB
的面积
=
矩形
ADLM
的面积
+
矩形MLEB的面积
∴
做三个边长分别为
a
、
b
、
c
的正方形,把它们拼成如图所示形状,使
H
、
C
、
B
三点在一条直线
上,连结
BF
、
CD.
过
C
作
CL
⊥
DE
,交
AB
于点
M
,交
DE
于点
L.
邹元治法
D
G
C
F
B
E
A
H
a
b
a
b
a
b
a
b
c
c
c
c
∵?RtΔHAE?≌?RtΔEBF,?∴?∠AHE?=?∠BEF.?
∵?∠AEH?+?∠AHE?=?90?,∴?∠AEH?+?∠BEF?=?90?.∴?∠HEF?=?180?―90?=?90?.?
∴?四边形EFGH是一个边长为c的正方形.?它的面积等于
∵?RtΔGDH?≌?RtΔHAE,?∴?∠HGD?=?∠EHA.?
∵?∠HGD?+?∠GHD?=?90?,∴?∠EHA?+?∠GHD?=?90?.?
又∵?∠GHE?=?90?,∴?∠DHA?=?90?+?90?=?180?.?
∴?ABCD是一个边长为a?+?b的正方形,它的面积等于∴??∴
做三个边长分别为
a
、
b
、
c
的正方形,把它们拼成如图所示形状,使
H
、
C
、
B
三点在一条直线
上,连结
BF
、
CD.
过
C
作
CL
⊥
DE
,交
AB
于点
M
,交
DE
于点
L.
典例分析
如图,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5m,梯子滑动后停在DE的位置上,如图2,测得BD长为0.5m,求梯子顶端A下落了多少米.
解法指导:
直角三角形中,已知一直角边和斜边是勾股定理的重要应用之一.勾股定理:的各种变式:.应牢固掌握,灵活应用.
分析:先利用勾股定理求出AC与CE的长则梯子顶端A下落的距离为AE=AC-CF.
解:在Rt△ABC中,
?
∴,∴AC=2(m).
?
在Rt△EDC中,,
∴
∴=2.25,∴CE=1.5(m),
?
∴AE=AC-CE=2-1.5=0.5(m)
?
答:梯子顶端A下落了0.5m.
A
C
E
D
B
如图,已知△ABC中,AD为高,且AB+CD=AC+BD,求证:AB=AC.
证明:∵三角形ABD和ACD是直角三角形,
∴AB2-BD2=AC2-CD2
①
又由AB+CD=AC+BD得:
AB-BD=AC-CD
②
由①②得:
AB+BD=AC+CD
③
联立公式②③得:
AB=AC.
A
C
D
B
例1
证明
∵四边形ABCD与四边形EFGH是正方形,
∴∠A=∠D=∠FEH=90°,EF=EH,
∴∠AEF+∠DEH=90°,∠AEF+∠AFE=90°,
∴∠DEH=∠AFE,
在△AEF和△DHE中,
EH=EF,
∠EAF=∠DAE
,∠DEH=∠AFE
∴△AEF≌△DHE,
∴AF=DE=b,
∵DE+AE=1,
∴a+b=1①,
∵SEFGH=EF2=AE2+AF2=
∴ab=
|b—a|=
故答案
D
H
C
G
B
F
A
E
已知:正方形ABCD的边长为1,正方形EFGH内接于ABCD,AE=
a,AF=b,且SEFGH=,则|b-a|的值。
例2
在三角形ABC中,∠A=90,M是BC中点,E.F分别在AC,AB上,且ME⊥MF,探索EF与BF,CE的等量关系,说明理由
例3
结论
证明:
延长EM至N使MN=EM连接BN,FN
∵BM=CM
∠EMC=∠BMN
∴△EMC全等于△BMN
∴∠MEC=∠MEB
∠ECM=∠MBN
EC=BN
∵∠ABC+∠ECM=90°
∴∠ABC+∠MBN=∠FBN=90°
∴
∵FM⊥EM
EM=MN
∴FN=EF
∴
课堂小结
1、了解勾股定理的发现以及其证明过程。
2、通过不同的证明法来掌握勾股定理的证明。
3、学会用面积法证明勾股定理。
4、勾股定理的应用。
随堂测验
1、已知直角三角形两边的长为3和4,则此三角形的周长为__________.
2、某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要????????
__________元.
?3、如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m.同时梯子的顶端B下降至B′,那么BB′(???
).
A.小于1m??
B.大于1m??
C.等于1m?
D.小于或等于1m
?4、将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为h
cm,则h的取值范围是(?
)
A.h≤17cm???
B.h≥8cm?
C.15cm≤h≤16cm?????
D.7cm≤h≤16cm
12或7
150a
A
D
拓展提高
1.
小明想测量教学楼的高度.他用一根绳子从楼顶垂下,发现绳子垂到地面后还多了2
m,当他把绳子的下端拉开6
m后,发现绳子下端刚好接触地面,则教学楼的高为(?????
).?
?
A.
8
m????
B.
10
m????
C.
12
m????
D.
14
m?
2.如果梯子的底端离建筑物9
m,那么15
m长的梯子可以到达建筑物的高度是(?????
).?
A.
10
m???
B.
11
m????
C.
12
m????
D.
13
m?
3.
直角三角形三边的长分别为3、4、x,则x可能取的值有(?????
).?
?
A.
1个????
B.
2
个????
C.
3个?????
D.
无数多个
4、直角三角形中,以直角边为边长的两个正方形的面积为7cm2,8
cm2,则以斜边为边长的正方形的面积为_________
cm2.
A
.C
B?
15
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
