青岛版八年级数学下册6.1.1平行四边形及其性质课件(共28张PPT)
文档属性
| 名称 | 青岛版八年级数学下册6.1.1平行四边形及其性质课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-27 23:23:47 | ||
图片预览



文档简介
(共28张PPT)
第六章平行四边形
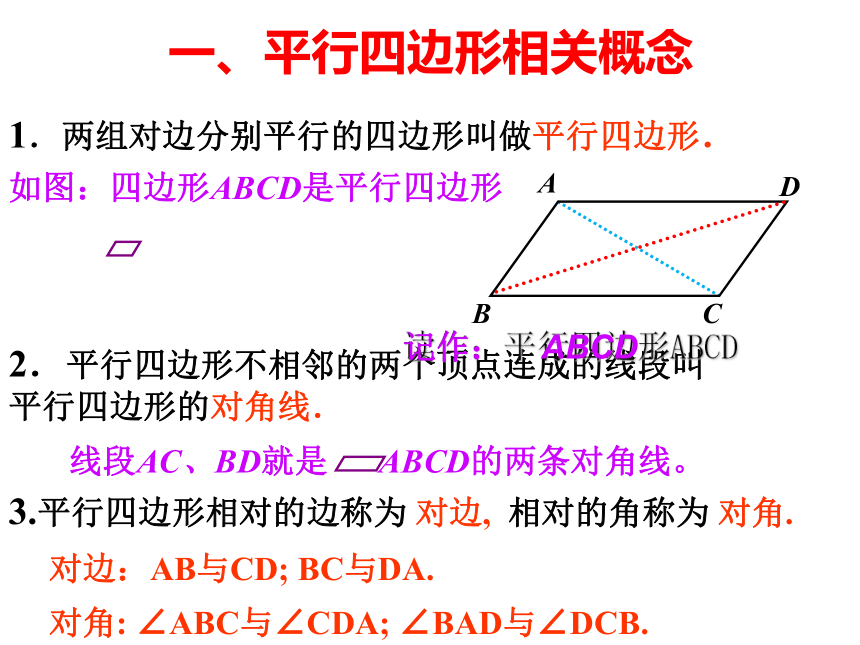
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为
对边,
相对的角称为
对角.
一、平行四边形相关概念
对边:AB与CD;
BC与DA.
对角:
∠ABC与∠CDA;
∠BAD与∠DCB.
读作:平行四边形ABCD
记作:
ABCD
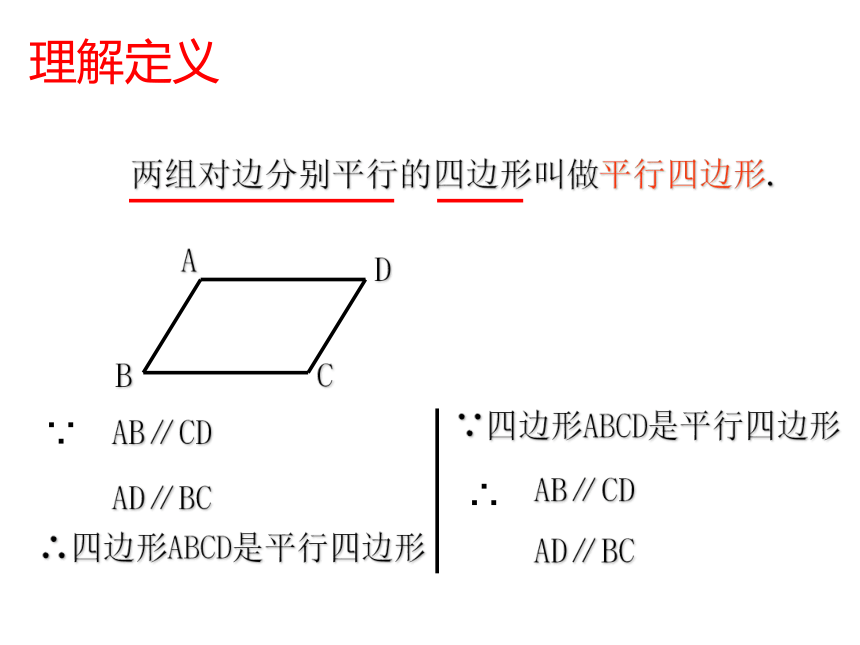
两组对边分别平行的四边形叫做平行四边形.
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
理解定义
6.1.1平行四边形及其性质
如图
∵四边形ABCD是平行四边形
性质1、定义
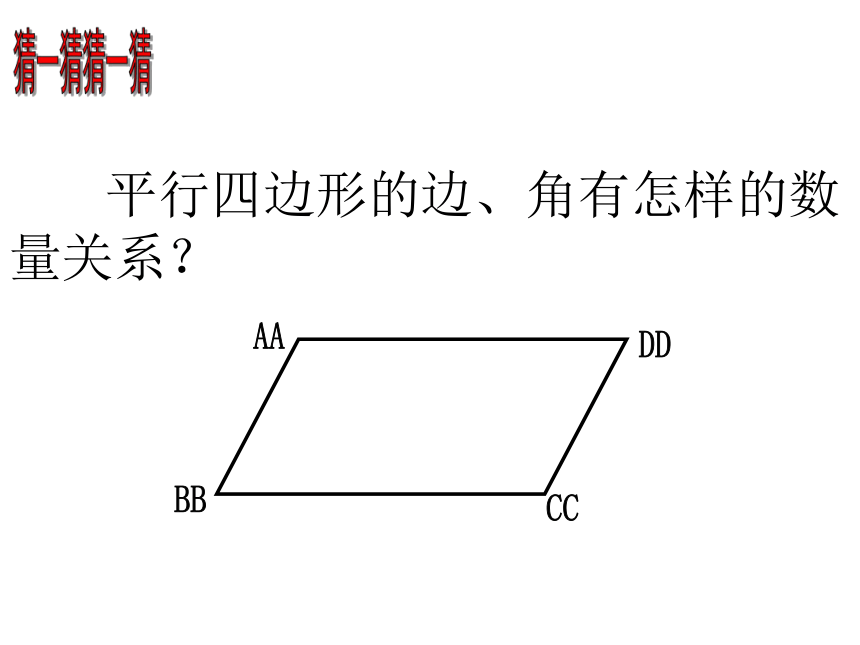
平行四边形的边、角有怎样的数量关系?
猜一猜
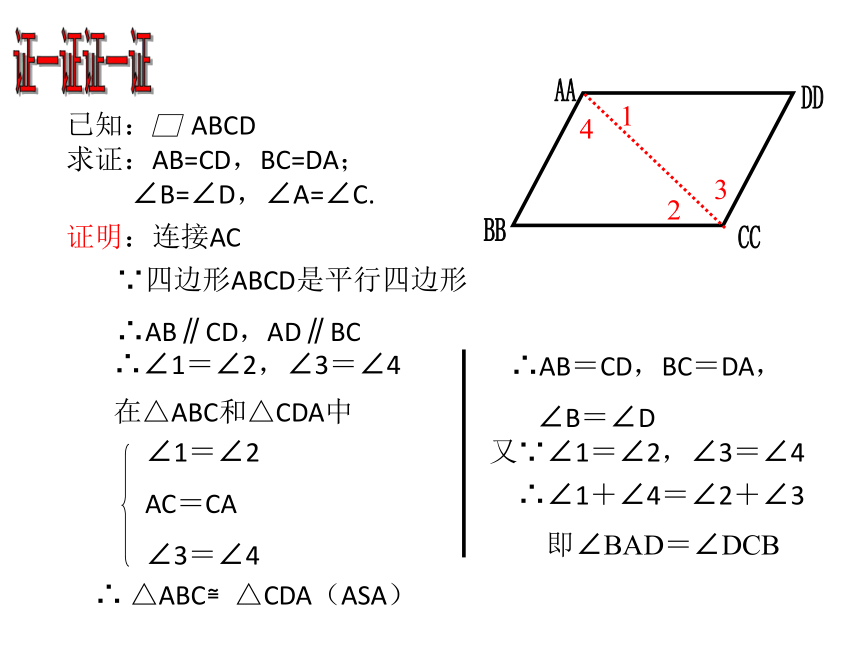
已知:
ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
证一证
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴
△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
几何语言:
性质2:平行四边形的两组对边分别相等
∵
四边形ABCD是平行四边形
∴
AB=CD,AD=BC.(平行四边形的对边相等)
或
∠A=
∠C,
∠B=
∠D(平行四边形的对角相等)
∠A=
∠C,
∠B=
∠D(平行四边形的对角相等)
性质3:平行四边形的两组对角分别相等
例1、如图
小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:∵
四边形ABCD是平行四边形
∴AB=CD,
AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴
AD=BC=10m
8cm
1.如图:在
ABCD中,根据已知你能得到哪
些结论?为什么?
32cm
30cm
56°
124°
124°
小结:平行四边形中知道其中一角可求出另外三个角的度数,
知道其中两边可求出另外两边的长度。
知识应用
4.如图,在
ABCD中,若BE平分∠ABC,则ED=
.
4cm
5cm
5cm
4cm
动手试一试
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O
钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
再看一遍
看一看
看一看
你有什么猜想?
结论
1.
ABCD绕它的中心O旋转180°后与自身重合,这时我们说
ABCD是
中心对称图形,点O叫对称中心。
你能证明
它吗?
根据刚才的旋转,你知道平行四边形的对角线有什么性质吗?
猜一猜
O
证明:
∵四边形ABCD是平行四边形,
∴
AD=BC,AD∥BC.
∴
∠1=∠2,∠3=∠4.
∴
△AOD≌△COB(ASA).
∴
OA=OC,OB=OD.
3
2
4
1
平行四边形的对角线互相平分.
证一证
性质4:
几何语言:
O
平行四边形的对角线互相平分.
选择:平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性
B、对角线互相平分
C、内角的为360度
D、外角和为360度
B
例2,如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及
ABCD的面积.
8
10
解:
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10,OA=OC
又∵OA=OC
∴
∴
∴S
=
BC×AC=8×6=48
ABCD
谁先会,谁展示
说一说,练一练
1、
如图,在
ABCD中,
BC=10cm,
AC=8cm,
BD=14cm,
(1)△
AOD的周长是多少?为什么?
(
2)
△
ABC与△
DBC的周长哪个长?长多少?
A
B
D
C
O
O
D
B
A
C
2.如图,在
ABCD中,
对角线AC﹑BD相交于点O,且AC+BD=20,
△AOB的周长等于15,
则CD=______.
5
3.如图,在
ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是
_________.
1<AD<9
4.
若平行四边形的一边长为5,则它的两条对角线长可以是(
)
A.
12和2
B.
3和4
C.
4和6
D.
4和8
O
D
B
A
C
D
4.如图,在平面直角坐标系中,
OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的
坐标为(
)
x
Y
C
O
(0,0)
B(5,0)
D(2,3)
A.
(3,7)
B.
(5,3)
C.
(7,3)
D.
(8,2)
C
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:
对边平行
对边相等
对角相等
邻角互补
对角线
3.解决平行四边形的有关问题经常连结对角线转化为三角形。
课堂小结
第六章平行四边形
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为
对边,
相对的角称为
对角.
一、平行四边形相关概念
对边:AB与CD;
BC与DA.
对角:
∠ABC与∠CDA;
∠BAD与∠DCB.
读作:平行四边形ABCD
记作:
ABCD
两组对边分别平行的四边形叫做平行四边形.
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
理解定义
6.1.1平行四边形及其性质
如图
∵四边形ABCD是平行四边形
性质1、定义
平行四边形的边、角有怎样的数量关系?
猜一猜
已知:
ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
证一证
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴
△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
几何语言:
性质2:平行四边形的两组对边分别相等
∵
四边形ABCD是平行四边形
∴
AB=CD,AD=BC.(平行四边形的对边相等)
或
∠A=
∠C,
∠B=
∠D(平行四边形的对角相等)
∠A=
∠C,
∠B=
∠D(平行四边形的对角相等)
性质3:平行四边形的两组对角分别相等
例1、如图
小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:∵
四边形ABCD是平行四边形
∴AB=CD,
AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴
AD=BC=10m
8cm
1.如图:在
ABCD中,根据已知你能得到哪
些结论?为什么?
32cm
30cm
56°
124°
124°
小结:平行四边形中知道其中一角可求出另外三个角的度数,
知道其中两边可求出另外两边的长度。
知识应用
4.如图,在
ABCD中,若BE平分∠ABC,则ED=
.
4cm
5cm
5cm
4cm
动手试一试
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O
钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
再看一遍
看一看
看一看
你有什么猜想?
结论
1.
ABCD绕它的中心O旋转180°后与自身重合,这时我们说
ABCD是
中心对称图形,点O叫对称中心。
你能证明
它吗?
根据刚才的旋转,你知道平行四边形的对角线有什么性质吗?
猜一猜
O
证明:
∵四边形ABCD是平行四边形,
∴
AD=BC,AD∥BC.
∴
∠1=∠2,∠3=∠4.
∴
△AOD≌△COB(ASA).
∴
OA=OC,OB=OD.
3
2
4
1
平行四边形的对角线互相平分.
证一证
性质4:
几何语言:
O
平行四边形的对角线互相平分.
选择:平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性
B、对角线互相平分
C、内角的为360度
D、外角和为360度
B
例2,如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及
ABCD的面积.
8
10
解:
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10,OA=OC
又∵OA=OC
∴
∴
∴S
=
BC×AC=8×6=48
ABCD
谁先会,谁展示
说一说,练一练
1、
如图,在
ABCD中,
BC=10cm,
AC=8cm,
BD=14cm,
(1)△
AOD的周长是多少?为什么?
(
2)
△
ABC与△
DBC的周长哪个长?长多少?
A
B
D
C
O
O
D
B
A
C
2.如图,在
ABCD中,
对角线AC﹑BD相交于点O,且AC+BD=20,
△AOB的周长等于15,
则CD=______.
5
3.如图,在
ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是
_________.
1<AD<9
4.
若平行四边形的一边长为5,则它的两条对角线长可以是(
)
A.
12和2
B.
3和4
C.
4和6
D.
4和8
O
D
B
A
C
D
4.如图,在平面直角坐标系中,
OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的
坐标为(
)
x
Y
C
O
(0,0)
B(5,0)
D(2,3)
A.
(3,7)
B.
(5,3)
C.
(7,3)
D.
(8,2)
C
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:
对边平行
对边相等
对角相等
邻角互补
对角线
3.解决平行四边形的有关问题经常连结对角线转化为三角形。
课堂小结
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
