人教高中数学选修2-3第一章 1.3.1二项式定理(一)课件(22张ppt)
文档属性
| 名称 | 人教高中数学选修2-3第一章 1.3.1二项式定理(一)课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 630.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-28 14:31:05 | ||
图片预览







文档简介
(共22张PPT)
二项式定理,又称牛顿二项式定理,由艾萨克·牛顿于1664、1665年间提出.
二项式定理在组合理论、开高次方、高阶等差数列求和,以及差分法中都有广泛的应用.
…
…
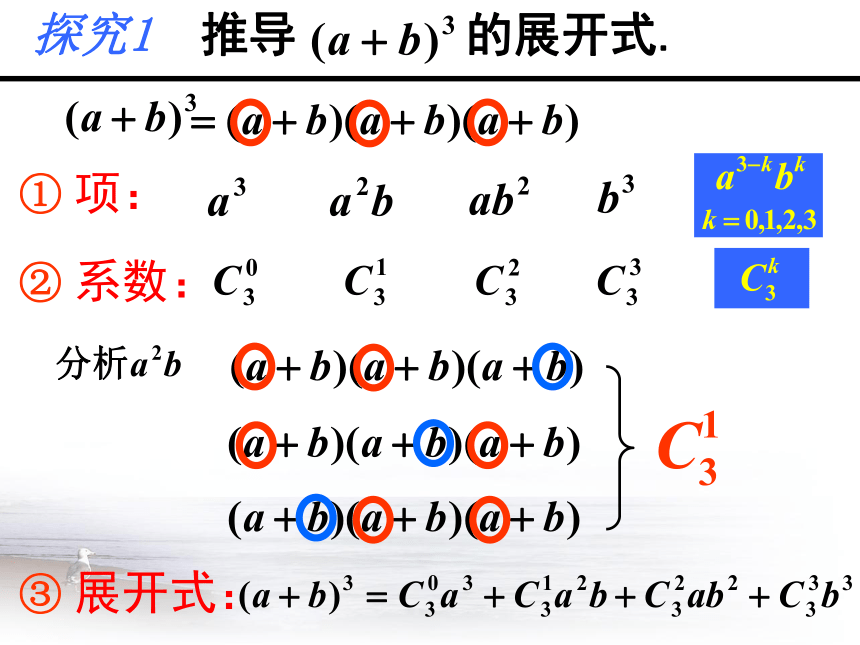
多项式乘法的再认识
①
项:
②
系数:
1
③
展开式:
探究2
仿照上述过程,推导
的展开式.
①项:
②系数:
L
L
③展开式:
④二项展开式的通项:
③二项式系数:
①项数:
②次数:
共有n+1项
各项的次数都等于n,
字母a按降幂排列,次数由n递减到0
,
字母b按升幂排列,次数由0递增到n
.
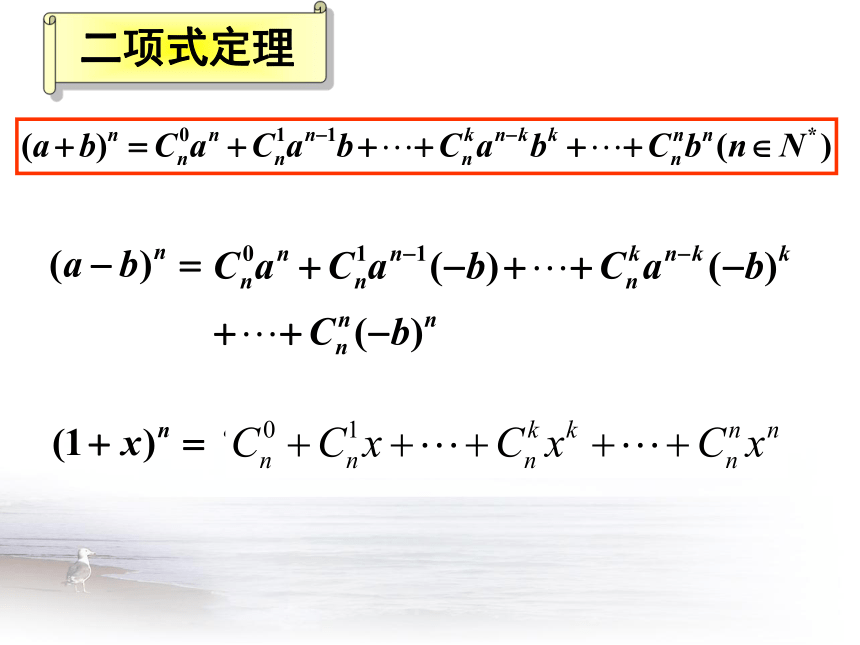
二项式定理
二项式定理
解:
直接展开
先化简后展开
解:
思考3:你能否直接求出展开式的第3项?
思考1:展开式的第3项的系数是多少?
思考2:展开式的第3项的二项式系数是多少?
解:
练习1
例2
(1)求(1+2x)7的展开式的第4项
注:1)注意对二项式定理的灵活应用
2)注意区别二项式系数与项的系数的概念
二项式系数:Cnr;
项的系数:二项式系数与数字系数的积
3)求二项式系数或项的系数的一种方法是将二项式展开
第4项的二项式系数
第4项的系数
例2
(1)求(1+2x)7的展开式的第4项的系数
解
(1)
(1+2x)7的展开式的第4项是
T3+1=C73?17-3?(2x)3
=35×23×x3
=280x3
分析:
先求出x3是展开式的哪一项,再求它的系数
例2
(1)求(1+2x)7的展开式的第4项
9-2r
=3
r
=3
x3系数是
(-1)3C93=-84
练习2、化简:
(x-1)4+4(x-1)3+6(x-1)2+4(x-1)+1.
实战演练
求(x+a)12的展开式中的倒数第4项
解:
练习3
(x+a)12的展开式有13项,倒数第4项是它的第10项
解:
练习
解:
展开式共有10项,中间两项是第5、6项。
练习
思维拓展
在(x-1)(x-2)(x-3)(x-4)
(x-5)的展开式中含x4项
的系数是
(
)
2.
求(x+2y+z)6的展开式中含xy2z3项的系数.
A.
-15
B.
85
C.
-120
D.
274
A
(2)二项展开式的通项:
1.二项式定理:
2.思想方法
(1)二项式系数:
(2)
用计数原理分析二项式的展开过程.
(1)
从特殊到一般的数学思维方式.
(3)
类比、等价转换的思想.
二项式定理,又称牛顿二项式定理,由艾萨克·牛顿于1664、1665年间提出.
二项式定理在组合理论、开高次方、高阶等差数列求和,以及差分法中都有广泛的应用.
…
…
多项式乘法的再认识
①
项:
②
系数:
1
③
展开式:
探究2
仿照上述过程,推导
的展开式.
①项:
②系数:
L
L
③展开式:
④二项展开式的通项:
③二项式系数:
①项数:
②次数:
共有n+1项
各项的次数都等于n,
字母a按降幂排列,次数由n递减到0
,
字母b按升幂排列,次数由0递增到n
.
二项式定理
二项式定理
解:
直接展开
先化简后展开
解:
思考3:你能否直接求出展开式的第3项?
思考1:展开式的第3项的系数是多少?
思考2:展开式的第3项的二项式系数是多少?
解:
练习1
例2
(1)求(1+2x)7的展开式的第4项
注:1)注意对二项式定理的灵活应用
2)注意区别二项式系数与项的系数的概念
二项式系数:Cnr;
项的系数:二项式系数与数字系数的积
3)求二项式系数或项的系数的一种方法是将二项式展开
第4项的二项式系数
第4项的系数
例2
(1)求(1+2x)7的展开式的第4项的系数
解
(1)
(1+2x)7的展开式的第4项是
T3+1=C73?17-3?(2x)3
=35×23×x3
=280x3
分析:
先求出x3是展开式的哪一项,再求它的系数
例2
(1)求(1+2x)7的展开式的第4项
9-2r
=3
r
=3
x3系数是
(-1)3C93=-84
练习2、化简:
(x-1)4+4(x-1)3+6(x-1)2+4(x-1)+1.
实战演练
求(x+a)12的展开式中的倒数第4项
解:
练习3
(x+a)12的展开式有13项,倒数第4项是它的第10项
解:
练习
解:
展开式共有10项,中间两项是第5、6项。
练习
思维拓展
在(x-1)(x-2)(x-3)(x-4)
(x-5)的展开式中含x4项
的系数是
(
)
2.
求(x+2y+z)6的展开式中含xy2z3项的系数.
A.
-15
B.
85
C.
-120
D.
274
A
(2)二项展开式的通项:
1.二项式定理:
2.思想方法
(1)二项式系数:
(2)
用计数原理分析二项式的展开过程.
(1)
从特殊到一般的数学思维方式.
(3)
类比、等价转换的思想.
