《三角形全等的判定复习》课件
图片预览

文档简介
(共29张PPT)
复习课
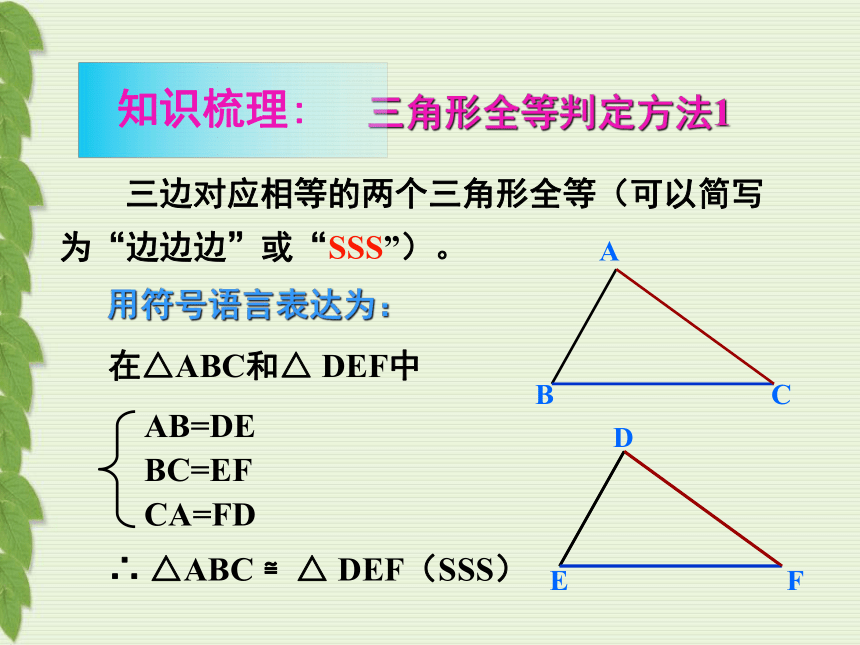
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
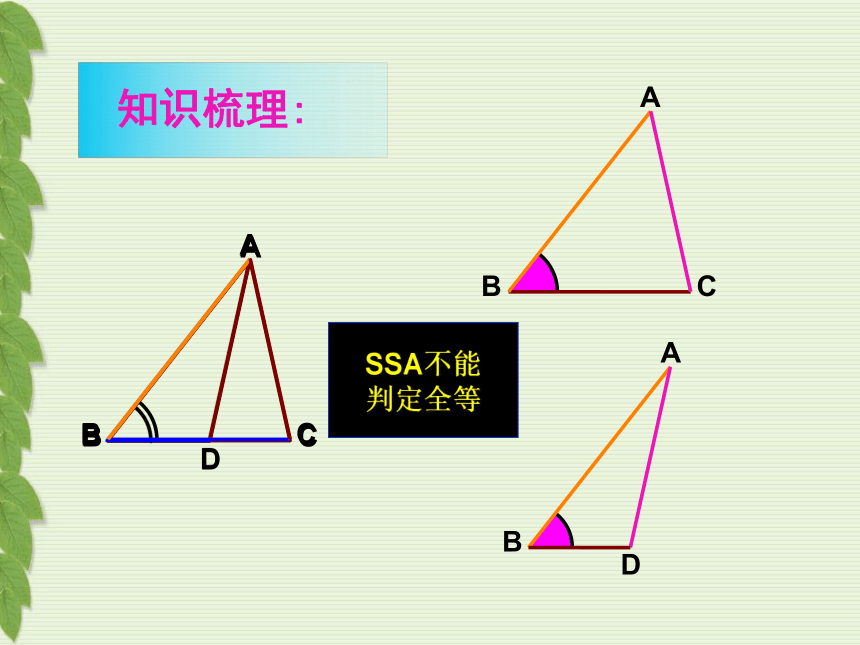
知识梳理:
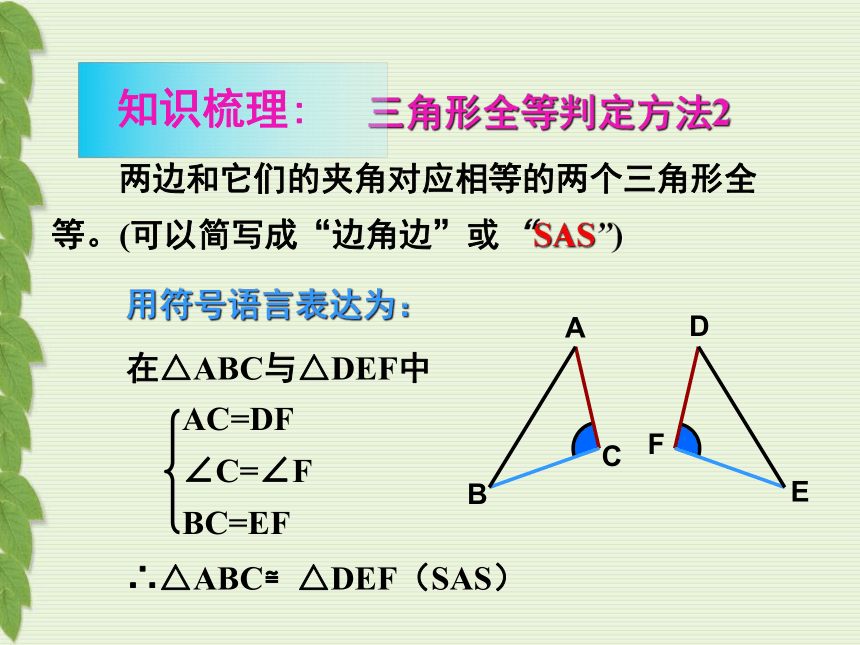
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
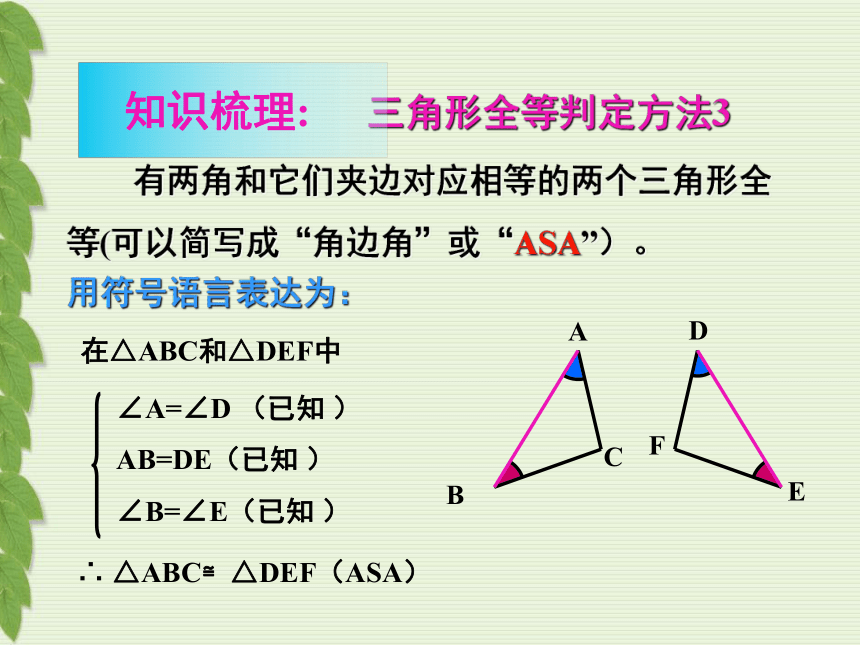
∠A=∠D (已知 )
AB=DE(已知 )
∠B=∠E(已知 )
在△ABC和△DEF中
∴ △ABC≌△DEF(ASA)
有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
用符号语言表达为:
F
E
D
C
B
A
三角形全等判定方法3
知识梳理:
知识梳理:
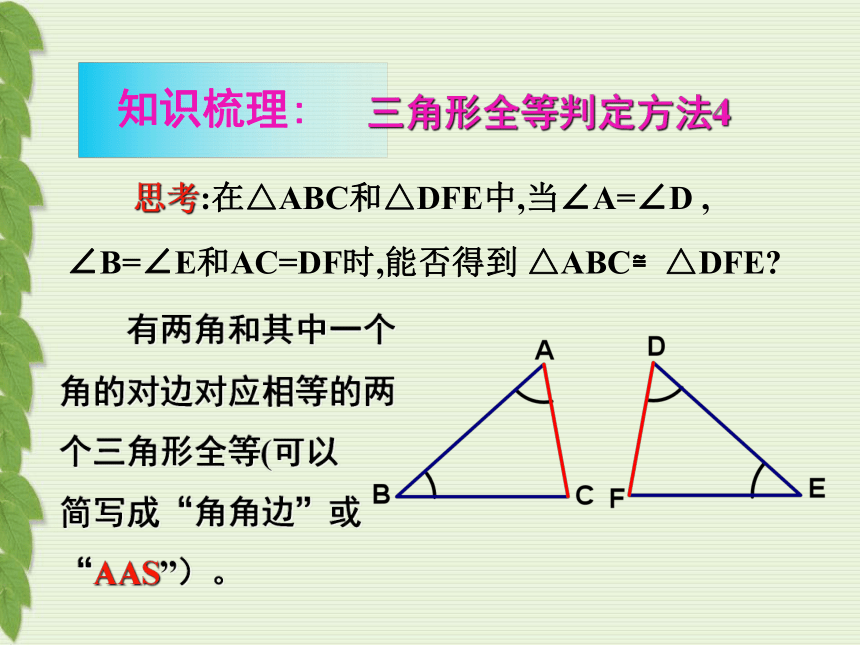
思考:在△ABC和△DFE中,当∠A=∠D , ∠B=∠E和AC=DF时,能否得到 △ABC≌△DFE
三角形全等判定方法4
有两角和其中一个角的对边对应相等的两个三角形全等(可以 简写成“角角边”或“AAS”)。
知识梳理:
A
B
D
A
B
C
SSA不能判定全等
A
B
C
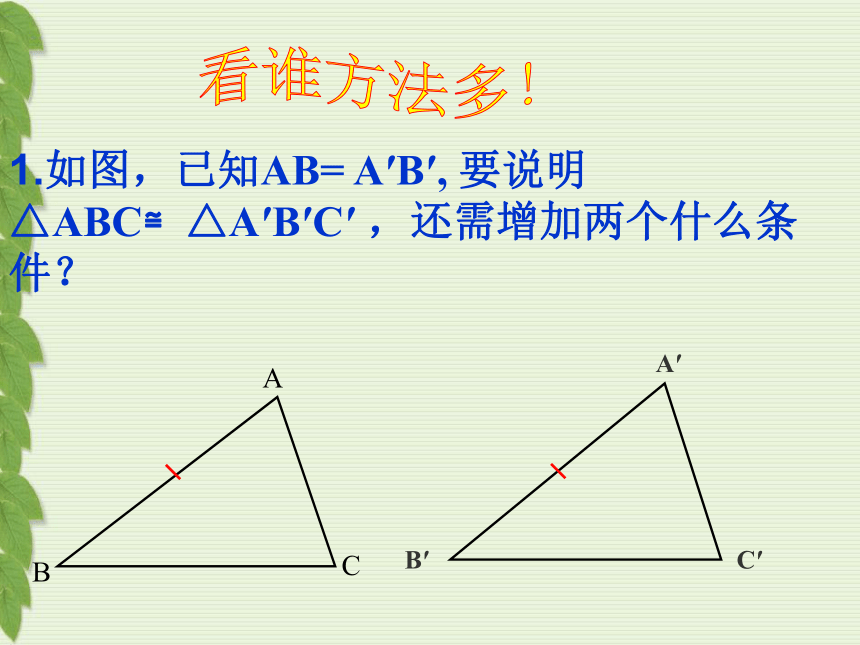
1.如图,已知AB= A′B′, 要说明△ABC≌△A′B′C′ ,还需增加两个什么条件?
A′
C′
B′
C
B
A
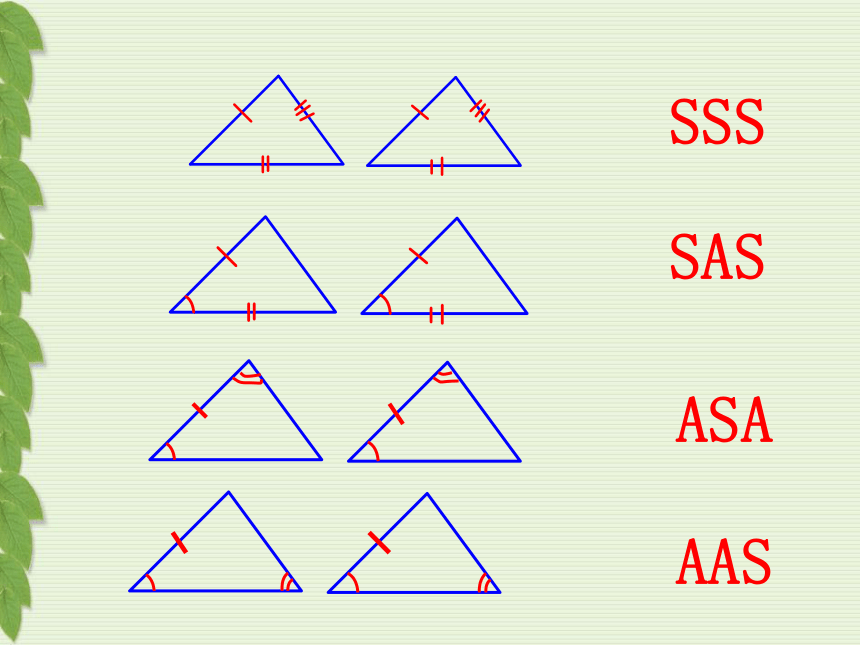
SSS
SAS
ASA
AAS
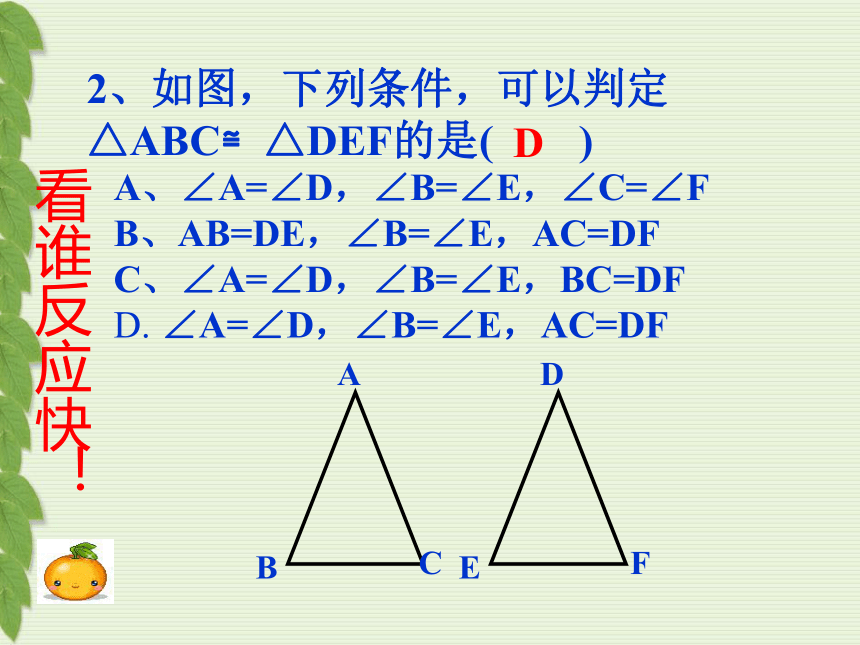
2、如图,下列条件,可以判定△ABC≌△DEF的是( )
D
A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
C、∠A=∠D,∠B=∠E,BC=DF
D. ∠A=∠D,∠B=∠E,AC=DF
A
B
C
D
E
F
看谁反应快!
问题1 已知:如图,AB=DE,AC=DF,
BE=CF,求证:∠A=∠D
①要证什么
③已有什么
④还缺什么
②需证什么
友情提示:
A
B
C
D
F
E
问题2、已知:如图∠1= ∠2, ∠ABC= ∠DCB。AC、DB 相交于点O。
求证:AB=DC
A
B
C
D
O
1
2
已知 :如图, AB=DB, ∠1=∠2,只需添加一个条件,就可得到△ABC≌△DBE.你有几种办法
B
C
A
E
D
1
2
典型例题:
例1 (2006浙江):如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .
分析:现在我们已知 A→∠CAB=∠DAB
①用SAS,需要补充条件AD=AC,
②用ASA,需要补充条件∠CBA=∠DBA,
③用AAS,需要补充条件∠C=∠D,
④此外,补充条件∠CBE=∠DBE也可以( )
SAS
ASA
AAS
S→ AB=AB(公共边) .
AD=AC
∠CBA=∠DBA
∠C=∠D
∠CBE=∠DBE
典型例题:
例2 (2006湖南株洲):如图,AE=AD,要使ΔABD≌ΔACE,请你增加一个条件是 .
分析:现在我们已知 S→ AE=AD
①用SAS,需要补充条件AB=AC,
②用ASA,需要补充条件∠ADB=∠AEC,
③用AAS,需要补充条件∠B=∠ C,
④此外,补充条件∠BDC=∠BEC也可以( )
SAS
ASA
AAS
(CD=BE行吗 )
A→∠A=∠A (公共角) .
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
∵∠1=∠2 (已知) ∴ ∠1+∠EAB = ∠2+ ∠EAB, 即∠BAC=∠EAD
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
AB=AE
∴ΔABC≌ΔAED(SAS)
AB=AE
①AB=AE
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
BC=ED
∴ΔABC与ΔAED不全等
BC=ED
②
BC=ED
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
∠C=∠D
∴ΔABC≌ΔAED(ASA)
∠C=∠D
③∠C=∠D,
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
∠B=∠E
∴ΔABC≌ΔAED(AAS)
∠B=∠E
∠B=∠E,
B
例4 (2007金华):如图, A,E,B,D在同一直线上, AB=DE,AC=DF,AC ∥ DF,在ΔABC和ΔDEF, (1)求证: ΔABC≌ΔDEF;
典型例题:
(1)证明:∵AC∥DF(已知) ∴∠A=∠D (两直线平行,内错角相等)
AB=DE(已知) ∠A=∠D(已证) AC=DF (已知)
∴ΔABC≌ΔDEF(SAS)
在ΔABC和ΔDEF中
例4 (2007金华):如图,A,E,B,D在同一直线上, 在ΔABC和ΔDEF中, AB=DE,AC=DF,AC∥DF, (2)你还可以得到的结论是 .(写出一个,不再添加其他线段,不再表注或使用其他字母)
典型例题:
解:根据”全等三角形的对应边(角)相等”可知:
②∠C=∠F,
③∠ABC=∠ DEF,
④ EF∥BC,
⑤AE=DB等
①BC=EF,
例5 (2005年昆明):如图,已知,AB=CD,CE=DF,AE=BF,则AE∥BF吗 为什么
典型例题:
证明: AE∥DF,理由是: ∵AB=CD(已知) ∴ AB+BC=CD+BC, 即AC=BD.
∴ ΔACE≌ΔBDF(SSS)
在ΔACE和ΔBDF中AC=BD(已证) CE=DF (已知) AE=BF (已知)
∴∠E=∠F(全等三角形的对应角相等) ∴ AE∥DF(内错角相等,两直线平行)
∵BE=EB(公共边)
又∵ AC∥ DB(已知) ∠DBE=∠CEB (两直线平行,内错角相等)
例6 (2006湖北黄冈):如图, AC∥ DB, AC=2DB,E是AC的中点,求证:BC=DE
典型例题:
证明:∵AC=2DB,AE=EC (已知) ∴DB=EC
DB=EC
∠DBE=∠CEB
BE=EB
∴ ΔDBE≌ΔCEB(SAS) ∴ BC=DE (全等三角形的对应边相等)
例7 (2006年烟台):如图在 ΔABC中,AD⊥BC于D,BE⊥AC于E,AD交BE于F,若BF=AC,那么∠ABC的大小是( )
典型例题:
A.40° B.50° C.60° D.45°
解: ∵AD⊥BC,BE⊥AC ∴∠ADB=∠ ADC= ∠BEC= 90°∴ ∠1=∠2在ΔACD和ΔBDF中
1
2
∠1=∠2(已证) AC= BF(已知) ∠ADC=∠ ADB (已证)
∴ ΔACD≌ΔBDF(ASA) ∴ AD=BD(全等三角形对应边相等)
∴ ∠ABC=45 °.选D
D
例8.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。
F
C
B
E
D
A
●
●
1.证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
小结:
3.注意正确地书写证明格式(顺序和对应关系).
请用三角形全等的知识自行设计一种测量底部不可到达物体的宽度(如河宽、池塘宽、山底部宽等等)的方案。
通过本节课学习你有什么收获
复习课
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
知识梳理:
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
∠A=∠D (已知 )
AB=DE(已知 )
∠B=∠E(已知 )
在△ABC和△DEF中
∴ △ABC≌△DEF(ASA)
有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
用符号语言表达为:
F
E
D
C
B
A
三角形全等判定方法3
知识梳理:
知识梳理:
思考:在△ABC和△DFE中,当∠A=∠D , ∠B=∠E和AC=DF时,能否得到 △ABC≌△DFE
三角形全等判定方法4
有两角和其中一个角的对边对应相等的两个三角形全等(可以 简写成“角角边”或“AAS”)。
知识梳理:
A
B
D
A
B
C
SSA不能判定全等
A
B
C
1.如图,已知AB= A′B′, 要说明△ABC≌△A′B′C′ ,还需增加两个什么条件?
A′
C′
B′
C
B
A
SSS
SAS
ASA
AAS
2、如图,下列条件,可以判定△ABC≌△DEF的是( )
D
A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
C、∠A=∠D,∠B=∠E,BC=DF
D. ∠A=∠D,∠B=∠E,AC=DF
A
B
C
D
E
F
看谁反应快!
问题1 已知:如图,AB=DE,AC=DF,
BE=CF,求证:∠A=∠D
①要证什么
③已有什么
④还缺什么
②需证什么
友情提示:
A
B
C
D
F
E
问题2、已知:如图∠1= ∠2, ∠ABC= ∠DCB。AC、DB 相交于点O。
求证:AB=DC
A
B
C
D
O
1
2
已知 :如图, AB=DB, ∠1=∠2,只需添加一个条件,就可得到△ABC≌△DBE.你有几种办法
B
C
A
E
D
1
2
典型例题:
例1 (2006浙江):如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .
分析:现在我们已知 A→∠CAB=∠DAB
①用SAS,需要补充条件AD=AC,
②用ASA,需要补充条件∠CBA=∠DBA,
③用AAS,需要补充条件∠C=∠D,
④此外,补充条件∠CBE=∠DBE也可以( )
SAS
ASA
AAS
S→ AB=AB(公共边) .
AD=AC
∠CBA=∠DBA
∠C=∠D
∠CBE=∠DBE
典型例题:
例2 (2006湖南株洲):如图,AE=AD,要使ΔABD≌ΔACE,请你增加一个条件是 .
分析:现在我们已知 S→ AE=AD
①用SAS,需要补充条件AB=AC,
②用ASA,需要补充条件∠ADB=∠AEC,
③用AAS,需要补充条件∠B=∠ C,
④此外,补充条件∠BDC=∠BEC也可以( )
SAS
ASA
AAS
(CD=BE行吗 )
A→∠A=∠A (公共角) .
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
∵∠1=∠2 (已知) ∴ ∠1+∠EAB = ∠2+ ∠EAB, 即∠BAC=∠EAD
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
AB=AE
∴ΔABC≌ΔAED(SAS)
AB=AE
①AB=AE
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
BC=ED
∴ΔABC与ΔAED不全等
BC=ED
②
BC=ED
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
∠C=∠D
∴ΔABC≌ΔAED(ASA)
∠C=∠D
③∠C=∠D,
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
典型例题:
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
∠B=∠E
∴ΔABC≌ΔAED(AAS)
∠B=∠E
∠B=∠E,
B
例4 (2007金华):如图, A,E,B,D在同一直线上, AB=DE,AC=DF,AC ∥ DF,在ΔABC和ΔDEF, (1)求证: ΔABC≌ΔDEF;
典型例题:
(1)证明:∵AC∥DF(已知) ∴∠A=∠D (两直线平行,内错角相等)
AB=DE(已知) ∠A=∠D(已证) AC=DF (已知)
∴ΔABC≌ΔDEF(SAS)
在ΔABC和ΔDEF中
例4 (2007金华):如图,A,E,B,D在同一直线上, 在ΔABC和ΔDEF中, AB=DE,AC=DF,AC∥DF, (2)你还可以得到的结论是 .(写出一个,不再添加其他线段,不再表注或使用其他字母)
典型例题:
解:根据”全等三角形的对应边(角)相等”可知:
②∠C=∠F,
③∠ABC=∠ DEF,
④ EF∥BC,
⑤AE=DB等
①BC=EF,
例5 (2005年昆明):如图,已知,AB=CD,CE=DF,AE=BF,则AE∥BF吗 为什么
典型例题:
证明: AE∥DF,理由是: ∵AB=CD(已知) ∴ AB+BC=CD+BC, 即AC=BD.
∴ ΔACE≌ΔBDF(SSS)
在ΔACE和ΔBDF中AC=BD(已证) CE=DF (已知) AE=BF (已知)
∴∠E=∠F(全等三角形的对应角相等) ∴ AE∥DF(内错角相等,两直线平行)
∵BE=EB(公共边)
又∵ AC∥ DB(已知) ∠DBE=∠CEB (两直线平行,内错角相等)
例6 (2006湖北黄冈):如图, AC∥ DB, AC=2DB,E是AC的中点,求证:BC=DE
典型例题:
证明:∵AC=2DB,AE=EC (已知) ∴DB=EC
DB=EC
∠DBE=∠CEB
BE=EB
∴ ΔDBE≌ΔCEB(SAS) ∴ BC=DE (全等三角形的对应边相等)
例7 (2006年烟台):如图在 ΔABC中,AD⊥BC于D,BE⊥AC于E,AD交BE于F,若BF=AC,那么∠ABC的大小是( )
典型例题:
A.40° B.50° C.60° D.45°
解: ∵AD⊥BC,BE⊥AC ∴∠ADB=∠ ADC= ∠BEC= 90°∴ ∠1=∠2在ΔACD和ΔBDF中
1
2
∠1=∠2(已证) AC= BF(已知) ∠ADC=∠ ADB (已证)
∴ ΔACD≌ΔBDF(ASA) ∴ AD=BD(全等三角形对应边相等)
∴ ∠ABC=45 °.选D
D
例8.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。
F
C
B
E
D
A
●
●
1.证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
小结:
3.注意正确地书写证明格式(顺序和对应关系).
请用三角形全等的知识自行设计一种测量底部不可到达物体的宽度(如河宽、池塘宽、山底部宽等等)的方案。
通过本节课学习你有什么收获
