《11.6、作三角形》教学课件
图片预览



文档简介
(共24张PPT)
豆豆书上的三角形被墨迹污染了一部分,他想在作业本上画出一个与书上完全一样的三角形,他该怎么办?
你能帮他画出来吗?
三角形的基本元素是____和____。
你会用尺规作一条线段等于已知线段吗?
自己动手试一试!
你会用尺规作一个角等于已知角吗?
你能利用尺规作一个三角形与已知三角形全等吗?
边
角
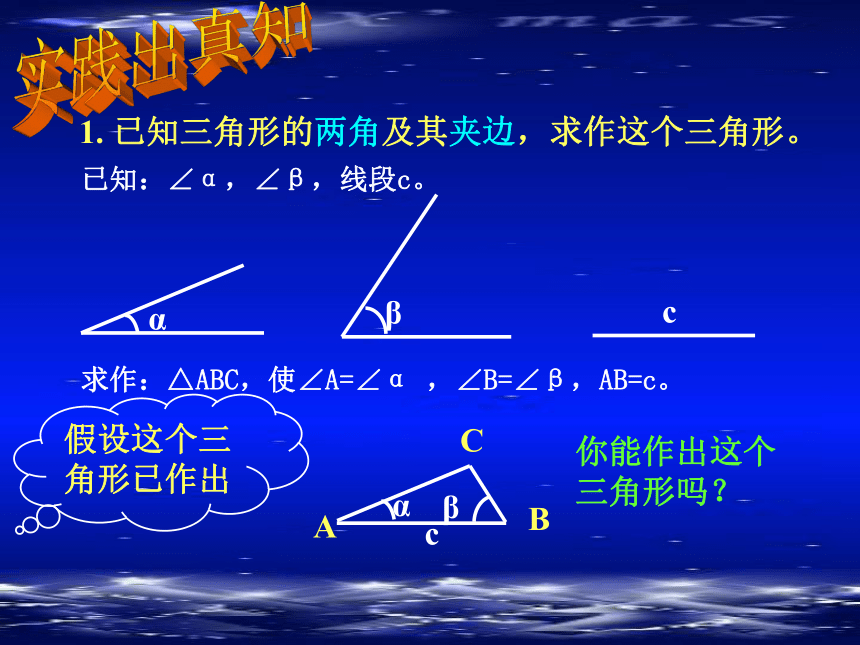
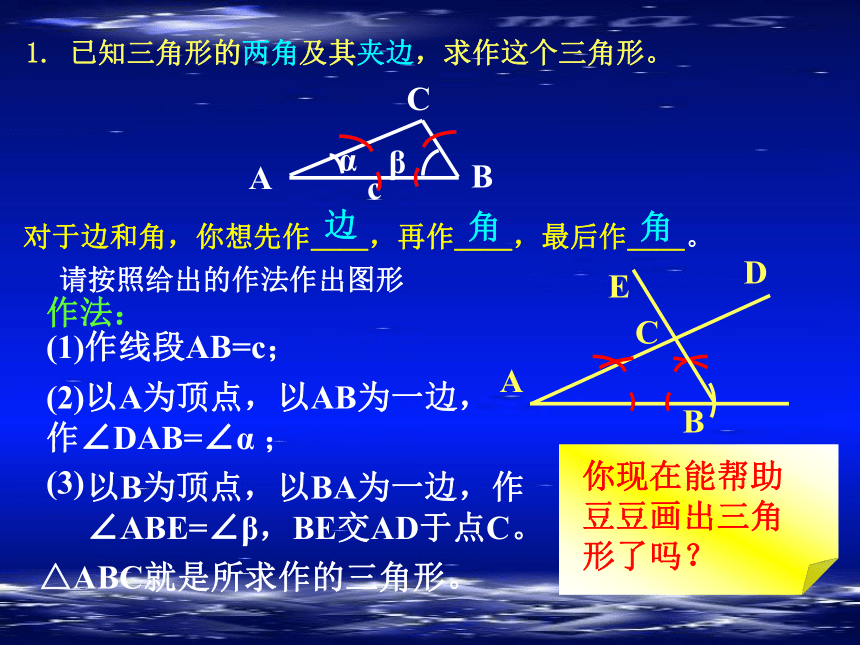
1. 已知三角形的两角及其夹边,求作这个三角形。
已知:∠α,∠β,线段c。
求作:△ABC,使∠A=∠α ,∠B=∠β,AB=c。
α
β
c
你能作出这个三角形吗?
α
β
A
B
C
c
假设这个三角形已作出
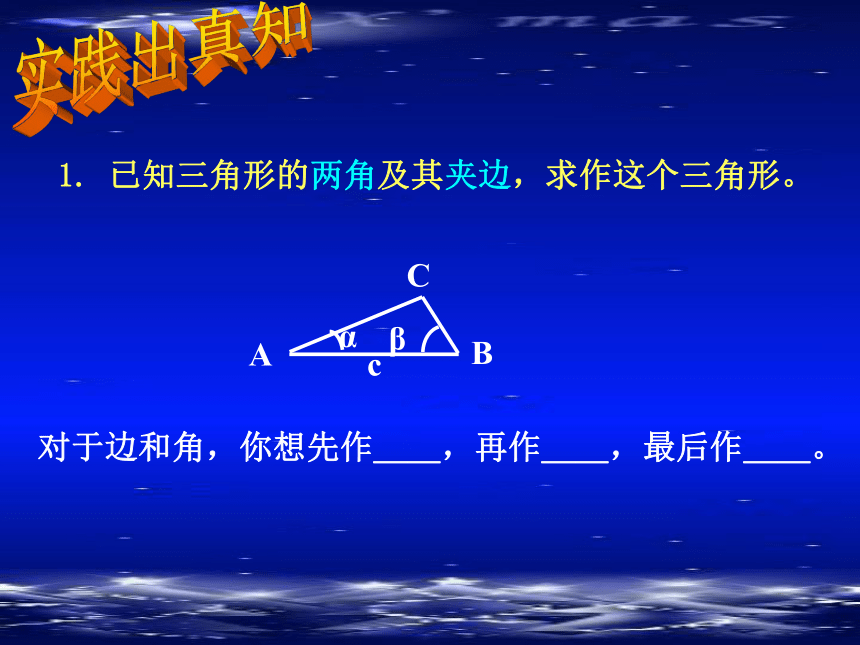
1. 已知三角形的两角及其夹边,求作这个三角形。
对于边和角,你想先作__,再作__,最后作__。
α
β
A
B
C
c
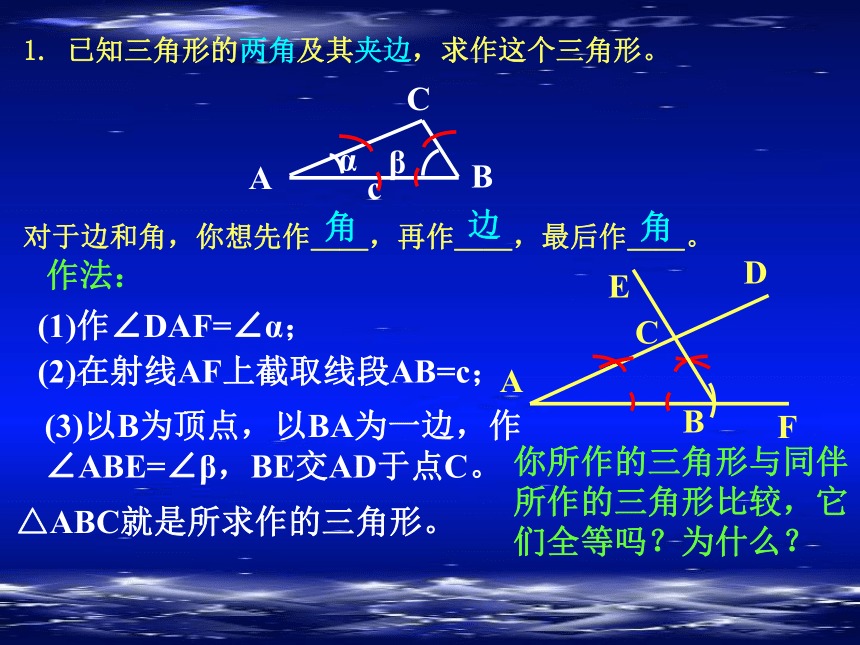
1. 已知三角形的两角及其夹边,求作这个三角形。
对于边和角,你想先作__,再作__,最后作__。
作法:
(1)作∠DAF=∠α;
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C。
△ABC就是所求作的三角形。
D
A
F
B
C
E
你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
α
β
A
B
C
c
角
角
边
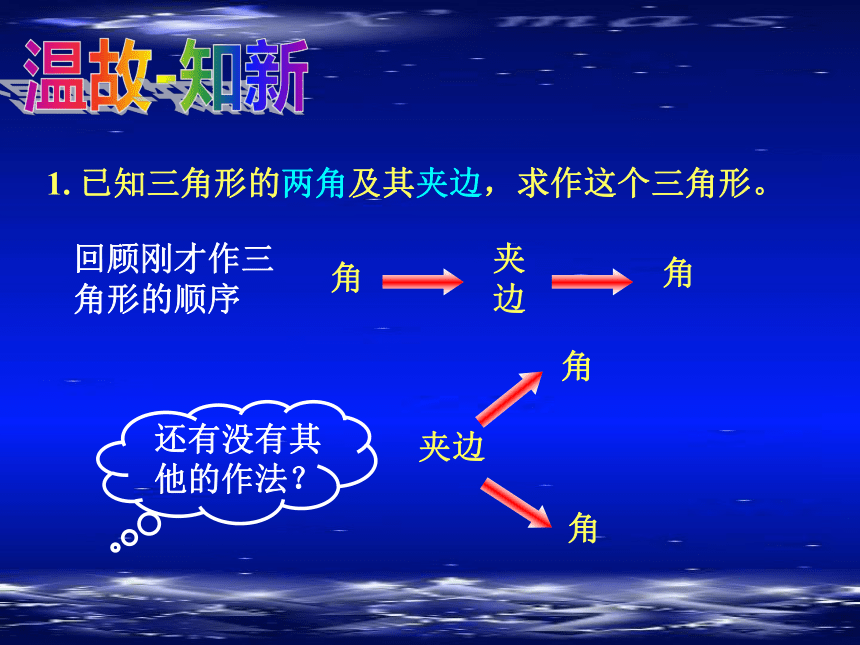
1. 已知三角形的两角及其夹边,求作这个三角形。
回顾刚才作三角形的顺序
角
角
夹边
夹边
角
角
还有没有其他的作法?
1. 已知三角形的两角及其夹边,求作这个三角形。
请按照给出的作法作出图形
作法:
(1)作线段AB=c;
(2)以A为顶点,以AB为一边,作∠DAB=∠α ;
以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C。
△ABC就是所求作的三角形。
D
A
B
C
E
(3)
α
β
A
B
C
c
对于边和角,你想先作__,再作__,最后作__。
角
角
边
你现在能帮助豆豆画出三角形了吗?
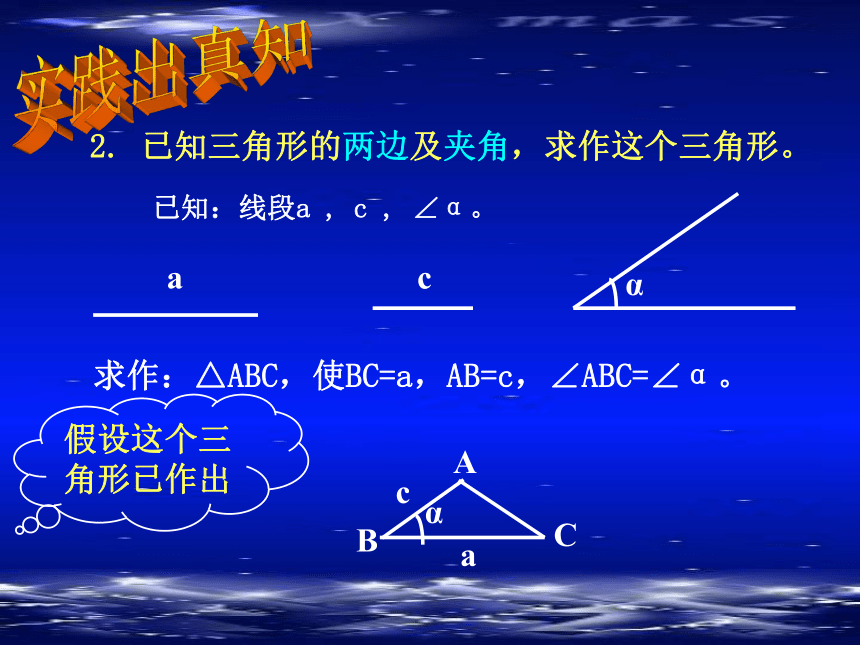
2. 已知三角形的两边及夹角,求作这个三角形。
已知:线段a , c , ∠α。
α
a
c
求作:△ABC,使BC=a,AB=c,∠ABC=∠α。
假设这个三角形已作出
B
A
C
α
a
c
B
C
D
A
作法:(1)作一条线段BC=a
(2)以B为顶点,以BC为一边,作角∠DBC=∠α
(3)在射线BD上截取线段BA=c
(4)连接AC
△ABC就是所求作的三角形。
你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
2. 已知三角形的两边及夹角,求作这个三角形。
对于边和角,你想先作__,再作__,最后作__。
α
a
c
B
A
C
a
c
α
边
角
边
请按照给出的作法作出图形
2. 已知三角形的两边及夹角,求作这个三角形。
回顾刚才作三角形的顺序
边
边
夹角
夹角
边
边
还有没有其他的作法?
2. 已知三角形的两边及夹角,求作这个三角形。
已知:线段a , c , ∠α。
α
a
c
求作:△ABC,使BC=a,AB=c,∠ABC=∠α。
作法:
(1)作∠DBE=∠α
(2)在射线BD,BE上分别截取BA=c,BC=a
(3)连接AC
△ABC就是所求作的三角形。
B
E
D
C
A
对于边和角,你想先作__,再作__,最后作__。
边
角
边
B
A
C
α
a
c
尝试自己作图,并用语言表述作法
(1)作∠······=∠ ······ ;
(2)在······上截取,使······ = ······ ;
(3)以···为顶点,以······为一边,作∠ ······ =∠ ······ ;
(4)作一条线段······ = ······ ;
(5)连接······ ,或连接······交······于点······ ;
(6)分别以··· , ···为圆心,以··· , ···为半径画弧,两弧交于···点;
······ ······ ······ ······
你知道的常用作图语言有哪些呢?
3. 已知三角形的三条边,求作这个三角形。
已知:线段 a,b,c。
求作:△ABC,使AB=c,AC=b,BC=a。
a
b
c
尝试自己分析并作出这个三角形、写出作法。
3.已知三角形的三条边,求作这个三角形。
已知:线段 a,b,c。
求作:△ABC,使AB=c,AC=b,BC=a。
(1)作一条线段BC=a;
(2)分别以B,C为圆心,以c,b为半径画弧,两弧交于A点;
(3)连接AB,AC。
△ABC就是所求作的三角形。
a
b
c
B
C
A
作法:
你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
经过前面的实践,我们如何来分析作图题呢?
1. 假设所求作的图形已经作出,并在草稿纸上作出草图;
2. 在草图上标出已给的边、角的对应位置;
3. 从草图中首先找出基本图形,由此确定作图的起始步骤;
4. 在3的基础上逐步向所求图形扩展。
1. 你能用尺规作一个直角三角形,使其两条直角边分别等于已知线段a,b吗?并写出作法。
a
b
分析:先在草纸上画出一个假设的“已作出的三角形”,会发现是“已知两边及夹角求作三角形”,所以按照此方法作图。
已知:直角,线段a,b
求作:直角三角形ABC,使BC=a,AC=b
作法:
(1)作∠DCE=90°
(2)在射线CD,CE上分别截取CB=a,CA=b
(3)连接AB
△ABC就是所求作的三角形。
C
D
E
B
A
2. 已知∠α和∠β,线段a,用尺规作一个三角形,使其一个内角等于∠α,另一个内角等于∠β ,且∠α的对边等于a。
α
a
提示:先作出一个角等于∠α+∠β,通过反向延长角的一边得到它的补角,即三角形中的第三个内角∠γ 。由此转换成已知∠β 和∠γ及其这两角的夹边a,求作这个三角形。
β
α
β
γ
β
γ
a
α
B
C
A
E
F
G
作法:1. 作∠α+∠β的补角∠γ
2. 作∠GBE=∠β
3. 在射线BE上截取BC=a
4. 以C为顶点,CB为一边作∠FCB=∠γ
5. 射线BG与射线CF相交于点A
△ABC就是所求作的三角形。
你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
已知线段a,b和∠α,求作△ABC,使其有一个内角等于∠α,且∠α的对边等于a,另有一边等于b。
a
b
α
分析:先在草纸上画出一个假设的“已作出的三角形”;然后在草图上标出已给的边、角的对应位置;再找出边与角,确定作图的顺序。
α
b
a
a
A
B
M
N
C
C'
作法:
1. 作∠MAN=∠α
2. 在射线AM上截取AB=b
3. 以B为圆心,以a为半径画弧,交AN于点C, C'
4. 连接BC,BC'
△ABC和△ABC'就是所求作的三角形。
同样是已知两边及一角,为什么会出现两个三角形呢?
你从中可以感悟到什么?
感悟:已知三角形的两边及一角并不都能只确定一个三角形。当已知两边及夹角时可以确定一个三角形,因此可以用来判定两个三角形全等;而当已知两边及一边的对角时,会画出两个不同的三角形,因此不能用来作为判别两个三角形全等的条件。
α
b
a
a
A
B
M
N
C
C'
a
c
α
两边及夹角
两边及一边的对角
B
E
D
C
A
谈谈你本节课的
收获与感受
豆豆书上的三角形被墨迹污染了一部分,他想在作业本上画出一个与书上完全一样的三角形,他该怎么办?
你能帮他画出来吗?
三角形的基本元素是____和____。
你会用尺规作一条线段等于已知线段吗?
自己动手试一试!
你会用尺规作一个角等于已知角吗?
你能利用尺规作一个三角形与已知三角形全等吗?
边
角
1. 已知三角形的两角及其夹边,求作这个三角形。
已知:∠α,∠β,线段c。
求作:△ABC,使∠A=∠α ,∠B=∠β,AB=c。
α
β
c
你能作出这个三角形吗?
α
β
A
B
C
c
假设这个三角形已作出
1. 已知三角形的两角及其夹边,求作这个三角形。
对于边和角,你想先作__,再作__,最后作__。
α
β
A
B
C
c
1. 已知三角形的两角及其夹边,求作这个三角形。
对于边和角,你想先作__,再作__,最后作__。
作法:
(1)作∠DAF=∠α;
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C。
△ABC就是所求作的三角形。
D
A
F
B
C
E
你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
α
β
A
B
C
c
角
角
边
1. 已知三角形的两角及其夹边,求作这个三角形。
回顾刚才作三角形的顺序
角
角
夹边
夹边
角
角
还有没有其他的作法?
1. 已知三角形的两角及其夹边,求作这个三角形。
请按照给出的作法作出图形
作法:
(1)作线段AB=c;
(2)以A为顶点,以AB为一边,作∠DAB=∠α ;
以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C。
△ABC就是所求作的三角形。
D
A
B
C
E
(3)
α
β
A
B
C
c
对于边和角,你想先作__,再作__,最后作__。
角
角
边
你现在能帮助豆豆画出三角形了吗?
2. 已知三角形的两边及夹角,求作这个三角形。
已知:线段a , c , ∠α。
α
a
c
求作:△ABC,使BC=a,AB=c,∠ABC=∠α。
假设这个三角形已作出
B
A
C
α
a
c
B
C
D
A
作法:(1)作一条线段BC=a
(2)以B为顶点,以BC为一边,作角∠DBC=∠α
(3)在射线BD上截取线段BA=c
(4)连接AC
△ABC就是所求作的三角形。
你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
2. 已知三角形的两边及夹角,求作这个三角形。
对于边和角,你想先作__,再作__,最后作__。
α
a
c
B
A
C
a
c
α
边
角
边
请按照给出的作法作出图形
2. 已知三角形的两边及夹角,求作这个三角形。
回顾刚才作三角形的顺序
边
边
夹角
夹角
边
边
还有没有其他的作法?
2. 已知三角形的两边及夹角,求作这个三角形。
已知:线段a , c , ∠α。
α
a
c
求作:△ABC,使BC=a,AB=c,∠ABC=∠α。
作法:
(1)作∠DBE=∠α
(2)在射线BD,BE上分别截取BA=c,BC=a
(3)连接AC
△ABC就是所求作的三角形。
B
E
D
C
A
对于边和角,你想先作__,再作__,最后作__。
边
角
边
B
A
C
α
a
c
尝试自己作图,并用语言表述作法
(1)作∠······=∠ ······ ;
(2)在······上截取,使······ = ······ ;
(3)以···为顶点,以······为一边,作∠ ······ =∠ ······ ;
(4)作一条线段······ = ······ ;
(5)连接······ ,或连接······交······于点······ ;
(6)分别以··· , ···为圆心,以··· , ···为半径画弧,两弧交于···点;
······ ······ ······ ······
你知道的常用作图语言有哪些呢?
3. 已知三角形的三条边,求作这个三角形。
已知:线段 a,b,c。
求作:△ABC,使AB=c,AC=b,BC=a。
a
b
c
尝试自己分析并作出这个三角形、写出作法。
3.已知三角形的三条边,求作这个三角形。
已知:线段 a,b,c。
求作:△ABC,使AB=c,AC=b,BC=a。
(1)作一条线段BC=a;
(2)分别以B,C为圆心,以c,b为半径画弧,两弧交于A点;
(3)连接AB,AC。
△ABC就是所求作的三角形。
a
b
c
B
C
A
作法:
你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
经过前面的实践,我们如何来分析作图题呢?
1. 假设所求作的图形已经作出,并在草稿纸上作出草图;
2. 在草图上标出已给的边、角的对应位置;
3. 从草图中首先找出基本图形,由此确定作图的起始步骤;
4. 在3的基础上逐步向所求图形扩展。
1. 你能用尺规作一个直角三角形,使其两条直角边分别等于已知线段a,b吗?并写出作法。
a
b
分析:先在草纸上画出一个假设的“已作出的三角形”,会发现是“已知两边及夹角求作三角形”,所以按照此方法作图。
已知:直角,线段a,b
求作:直角三角形ABC,使BC=a,AC=b
作法:
(1)作∠DCE=90°
(2)在射线CD,CE上分别截取CB=a,CA=b
(3)连接AB
△ABC就是所求作的三角形。
C
D
E
B
A
2. 已知∠α和∠β,线段a,用尺规作一个三角形,使其一个内角等于∠α,另一个内角等于∠β ,且∠α的对边等于a。
α
a
提示:先作出一个角等于∠α+∠β,通过反向延长角的一边得到它的补角,即三角形中的第三个内角∠γ 。由此转换成已知∠β 和∠γ及其这两角的夹边a,求作这个三角形。
β
α
β
γ
β
γ
a
α
B
C
A
E
F
G
作法:1. 作∠α+∠β的补角∠γ
2. 作∠GBE=∠β
3. 在射线BE上截取BC=a
4. 以C为顶点,CB为一边作∠FCB=∠γ
5. 射线BG与射线CF相交于点A
△ABC就是所求作的三角形。
你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
已知线段a,b和∠α,求作△ABC,使其有一个内角等于∠α,且∠α的对边等于a,另有一边等于b。
a
b
α
分析:先在草纸上画出一个假设的“已作出的三角形”;然后在草图上标出已给的边、角的对应位置;再找出边与角,确定作图的顺序。
α
b
a
a
A
B
M
N
C
C'
作法:
1. 作∠MAN=∠α
2. 在射线AM上截取AB=b
3. 以B为圆心,以a为半径画弧,交AN于点C, C'
4. 连接BC,BC'
△ABC和△ABC'就是所求作的三角形。
同样是已知两边及一角,为什么会出现两个三角形呢?
你从中可以感悟到什么?
感悟:已知三角形的两边及一角并不都能只确定一个三角形。当已知两边及夹角时可以确定一个三角形,因此可以用来判定两个三角形全等;而当已知两边及一边的对角时,会画出两个不同的三角形,因此不能用来作为判别两个三角形全等的条件。
α
b
a
a
A
B
M
N
C
C'
a
c
α
两边及夹角
两边及一边的对角
B
E
D
C
A
谈谈你本节课的
收获与感受
