沪教版四上 5.4 角的度量 课件 (共17张PPT)
文档属性
| 名称 | 沪教版四上 5.4 角的度量 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 166.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-28 17:22:01 | ||
图片预览






文档简介
角的度量
学习目标:
1.知道度、分、秒,会进行它们之间的简单换算,并会通过角度比较角的大小。
2.回顾直角、锐角、钝角的概念。
3.会计算两个角的和、差。
4.记住余角和补角的概念,认识余角和补角的性质。
一、角的度量单位
角的度量单位是度、分、秒,是六十进制
1°的60分之一为1分,记作“1′ ”,即1°=60′
1′的60分之一为1秒,记作“1″ ”,即1′=60″
1个周角的360分之一是1度的角,记作 “1°”
例计算:
把18°25′12 ″化成用度表示的角。
解:
所以18°25′ 12″ =___________。
先把12″ 化成分,即12″ =(12? )=0.2′
再把(25+0.2)′化成度,即
(25+0.2)′=(25.2? )°=0.42°,
18.42°
1
60
1
60
4
15
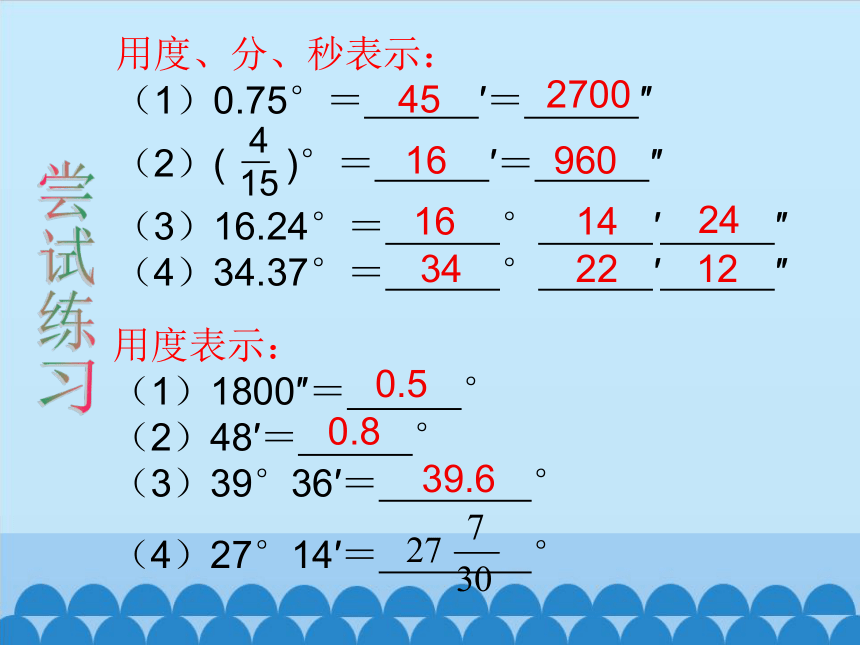
用度、分、秒表示:
(1)0.75°= ′= ″
(2)( - )°= ′= ″
(3)16.24°= ° ′ ″
(4)34.37°= ° ′ ″
用度表示:
(1)1800″= °
(2)48′= °
(3)39°36′= °
(4)27°14′= °
45
2700
16
960
16
14
24
34
22
12
0.5
0.8
39.6
尝试练习
例1
48°22′13″与48.37°哪个大?
解:
0.37°是十进制表示的,因此可先将0.37°用分、秒表示:
0.37°=60′× 0.37=22.2′
0.2′=60″×0.2=12″
所以0.37°=22′+0.2′=22′12″
因为22′12″< 22′13″
所以48.37°< 48°22′13″
回顾
1.周角、平角、直角
二、小于180°的角的分类
2.小于180°的角分为:
直角、锐角和钝角
分别确定四个城市相应钟表上时针与分针所成角的度数 ,它们分别是直角、锐角还是钝角?
巴黎时间 伦敦时间 北京时间 东京时间
30°
0°
120°
90°
锐角 钝角 直角
试一试
例2
已知∠α=37°50′ ,∠β=52°10′
求∠α+∠β与∠α-∠β
解:
因为∠α=37°50′ ,∠β=52°10′
所以∠α+∠β= 37°50′+ 52°10′
=90°
∠α-∠β = 37°50′- 52°10′
= 14°20′
三、计算两个角的和、差
四、余角和补角的性质
1.余角和补角的定义
如果两个角的和是90°,那么这两个角互为余角,简称 “互余”。
如果两个角的和是180°,那么这两个角互为补角,简称“互补”。
)
)
A
B
C
O
2
1
)
(
2
1
A
O
B
C
图1
)
(
A
B
O
D
C
图2
图3
在图1、图2、图3中找出互余的角和互补的角。
1.余角和补角的性质
同角或等角的余角相等
同角或等角的补角相等
)
)
)
)
1
2
3
4
A
B
C
D
E
O
已知,如图
∠AOC= ∠BOD
= ∠COE=90 °,
找出(1)互余的角;
(2)互补的角;
(3)相等的角。
(直角均除外)
(1) ∠1与∠3, ∠1与∠4, ∠1与∠3, ∠1与∠4;
(2) ∠1、 ∠2与∠AOD, ∠3、 ∠4与∠BOE;
(3) ∠1=∠2, ∠3= ∠4
小组讨论:
1.下列各对图形一定是互为余角的是( )
A
B
C
D
练习
2.如果 ,那么的补角等于( )
A. 20° B.70° C.110° D.160°
B
D
练习
3.∠α与∠β的度数分别是2m-67和68-m,且∠α与∠β都是∠γ 的补角,那么∠α与∠β的关系是( )。
A.互余但不相等 B.互为补角
C.相等但不互余 D.互余且相等
C
课堂小结:
本节课学习了以下内容
1.角的度量单位——度、分、秒,以及它们之间的换算。
2.直角、锐角、钝角的概念。
3.计算两个角的和、差。
4.余角和补角的概念,余角和补角的性质。
作业提示
⒈复习本节课内容。
⒉第15页课本习题。
谢 谢
学习目标:
1.知道度、分、秒,会进行它们之间的简单换算,并会通过角度比较角的大小。
2.回顾直角、锐角、钝角的概念。
3.会计算两个角的和、差。
4.记住余角和补角的概念,认识余角和补角的性质。
一、角的度量单位
角的度量单位是度、分、秒,是六十进制
1°的60分之一为1分,记作“1′ ”,即1°=60′
1′的60分之一为1秒,记作“1″ ”,即1′=60″
1个周角的360分之一是1度的角,记作 “1°”
例计算:
把18°25′12 ″化成用度表示的角。
解:
所以18°25′ 12″ =___________。
先把12″ 化成分,即12″ =(12? )=0.2′
再把(25+0.2)′化成度,即
(25+0.2)′=(25.2? )°=0.42°,
18.42°
1
60
1
60
4
15
用度、分、秒表示:
(1)0.75°= ′= ″
(2)( - )°= ′= ″
(3)16.24°= ° ′ ″
(4)34.37°= ° ′ ″
用度表示:
(1)1800″= °
(2)48′= °
(3)39°36′= °
(4)27°14′= °
45
2700
16
960
16
14
24
34
22
12
0.5
0.8
39.6
尝试练习
例1
48°22′13″与48.37°哪个大?
解:
0.37°是十进制表示的,因此可先将0.37°用分、秒表示:
0.37°=60′× 0.37=22.2′
0.2′=60″×0.2=12″
所以0.37°=22′+0.2′=22′12″
因为22′12″< 22′13″
所以48.37°< 48°22′13″
回顾
1.周角、平角、直角
二、小于180°的角的分类
2.小于180°的角分为:
直角、锐角和钝角
分别确定四个城市相应钟表上时针与分针所成角的度数 ,它们分别是直角、锐角还是钝角?
巴黎时间 伦敦时间 北京时间 东京时间
30°
0°
120°
90°
锐角 钝角 直角
试一试
例2
已知∠α=37°50′ ,∠β=52°10′
求∠α+∠β与∠α-∠β
解:
因为∠α=37°50′ ,∠β=52°10′
所以∠α+∠β= 37°50′+ 52°10′
=90°
∠α-∠β = 37°50′- 52°10′
= 14°20′
三、计算两个角的和、差
四、余角和补角的性质
1.余角和补角的定义
如果两个角的和是90°,那么这两个角互为余角,简称 “互余”。
如果两个角的和是180°,那么这两个角互为补角,简称“互补”。
)
)
A
B
C
O
2
1
)
(
2
1
A
O
B
C
图1
)
(
A
B
O
D
C
图2
图3
在图1、图2、图3中找出互余的角和互补的角。
1.余角和补角的性质
同角或等角的余角相等
同角或等角的补角相等
)
)
)
)
1
2
3
4
A
B
C
D
E
O
已知,如图
∠AOC= ∠BOD
= ∠COE=90 °,
找出(1)互余的角;
(2)互补的角;
(3)相等的角。
(直角均除外)
(1) ∠1与∠3, ∠1与∠4, ∠1与∠3, ∠1与∠4;
(2) ∠1、 ∠2与∠AOD, ∠3、 ∠4与∠BOE;
(3) ∠1=∠2, ∠3= ∠4
小组讨论:
1.下列各对图形一定是互为余角的是( )
A
B
C
D
练习
2.如果 ,那么的补角等于( )
A. 20° B.70° C.110° D.160°
B
D
练习
3.∠α与∠β的度数分别是2m-67和68-m,且∠α与∠β都是∠γ 的补角,那么∠α与∠β的关系是( )。
A.互余但不相等 B.互为补角
C.相等但不互余 D.互余且相等
C
课堂小结:
本节课学习了以下内容
1.角的度量单位——度、分、秒,以及它们之间的换算。
2.直角、锐角、钝角的概念。
3.计算两个角的和、差。
4.余角和补角的概念,余角和补角的性质。
作业提示
⒈复习本节课内容。
⒉第15页课本习题。
谢 谢
