人教版数学四年级上册 6.10《商的变化规律》课件(19张ppt)
文档属性
| 名称 | 人教版数学四年级上册 6.10《商的变化规律》课件(19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 707.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-29 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
除数是两位数的除法
6
人教版·四年级上册
第10课时 商的变化规律
看谁算得又对又快?
30÷10 =
40×20=
3
800
270÷30=
9
300×5=
1500
一、新课引入
150 × 24 =
3600
15 × 24 = 360
一个因数不变,另一个因数乘(或除以)几(0除外),积也随着乘(或除以)几。
积的变化规律:
看谁算得又对又快?
问题:我们都知道乘法和除法有着密切的联系,乘法中有着像 “积的变化规律”,那在除法中是否也有规律呢?
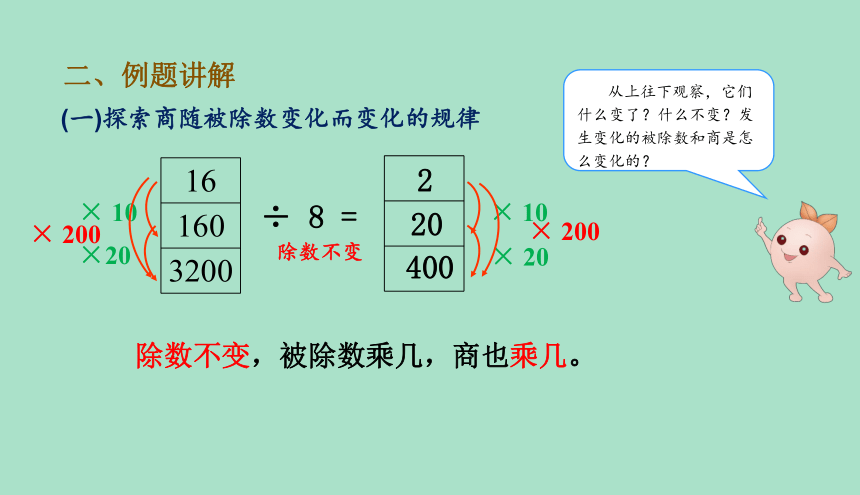
从上往下观察,它们什么变了?什么不变?发生变化的被除数和商是怎么变化的?
(一)探索商随被除数变化而变化的规律
二、例题讲解
16
160
3200
÷ 8 =
2
20
400
× 10
除数不变
× 10
×20
× 20
× 200
× 200
除数不变,被除数乘几,商也乘几。
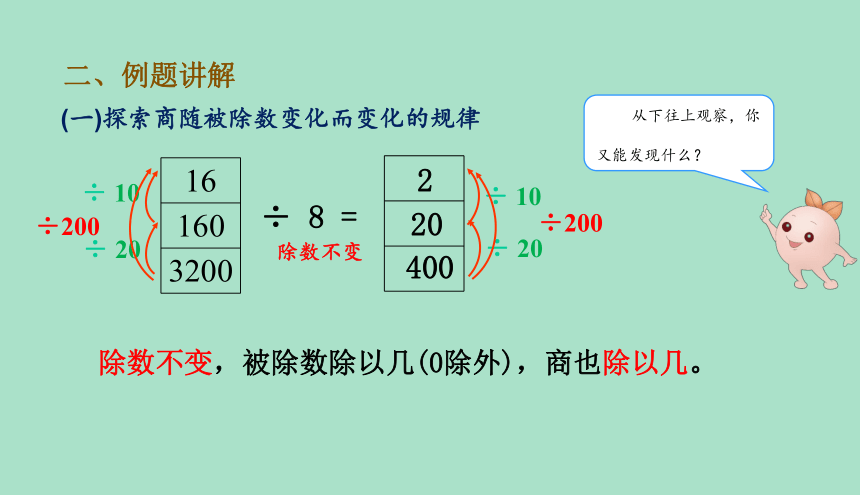
(一)探索商随被除数变化而变化的规律
二、例题讲解
16
160
3200
÷ 8 =
2
20
400
除数不变
除数不变,被除数除以几(0除外),商也除以几。
÷ 20
÷ 10
÷ 20
÷ 10
÷200
÷200
从下往上观察,你又能发现什么?
除数不变,
被除数乘(或除以)几(0除外),
商也随着乘(或除以)几。
被除数不变,商 除数
相同变
二、例题讲解
(一)探索商随被除数变化而变化的规律
二、例题讲解
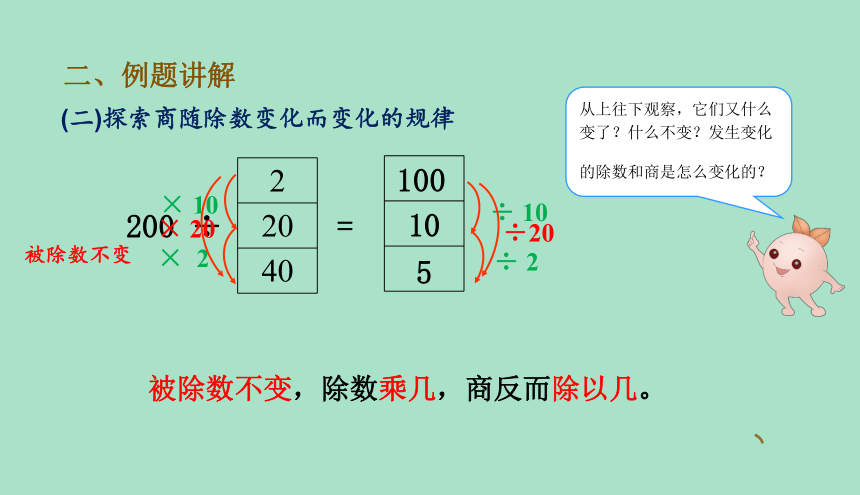
从上往下观察,它们又什么变了?什么不变?发生变化的除数和商是怎么变化的?
(二)探索商随除数变化而变化的规律
2
20
40
200 ÷ =
100
10
5
× 10
被除数不变
× 2
÷ 10
÷ 2
× 20
÷20
被除数不变,除数乘几,商反而除以几。
二、例题讲解
从下往上观察,你又能发现什么?
(二)探索商随除数变化而变化的规律
2
20
40
200 ÷ =
100
10
5
被除数不变
被除数不变,除数除以几(0除外),商反而乘几。
÷ 2
× 2
÷ 10
× 10
÷ 20
× 20
被除数不变,
除数 乘(或除以)几(0除外),
商反而除以(或乘)几。
被除数不变,商 除数
相反变
二、例题讲解
(二)探索商随除数变化而变化的规律
6 ÷ 3 = 2
60 ÷ 30 = 2
600 ÷ 300 = 2
①
③
②
× 10
× 10
× 10
× 10
×100
× 100
被除数和除数同时乘一个相同的数,商不变。
什么变了?什么不变?
问题:从上往下观察,它们什么变了?什么不变?发生变化的被除数和除数是怎么变的?
二、例题讲解
(三)探索商不变的规律
6 ÷ 3 = 2
60 ÷ 30 = 2
600 ÷ 300 = 2
①
③
②
÷10
÷10
÷10
÷10
÷100
÷100
被除数和除数同时除以一个相同的数,商不变。
什么变了?什么不变?
问题:从下往上观察呢?你又有什么发现?
二、例题讲解
(三)探索商不变的规律
12 ÷ 3 = 4
48 ÷ 12 =
×4
×4
4
360 ÷ 30 = 12
36 ÷ ( ) = 12
÷10
÷10
3
( )
(1)
(2)
80 ÷ 40 = 2
( ) ÷ ( ) = 2
( )
( )
(3)
问题:1.第3小题要使商不变,你想让被除数和除数同时做怎样的变化?同时乘和除以一个相同的数,这个数为任何数都行吗?哪个数不行?
2.所以我们总结出的这条规律必须给它加上一个条件“0除外”。
二、例题讲解
(三)探索商不变的规律
被除数和除数同时乘(或除以)一个相同的数(0除外),商不变。
商不变的性质
二、例题讲解
(三)探索商不变的规律
1.根据每组第一题的商,写出下面两题的商。
72 ÷ 9 =
720 ÷ 90 =
7200÷900 =
3600 ÷ 40 = 90
3600 ÷ 8 =
7200 ÷ 40 =
8
8
8
450
180
三、新知运用
(1)一个除法算式,被除数乘15,要使商不变,除数也要乘15。( )
(2)如果被除数不变,除数乘4,商也随着乘4。 ( )
√
×
2.我是小判官。
(3)一个除法算式的被除数、除数都除以3以后,商是20,那么原来的商是60。 ( )
×
我来答!
(1)被除数乘2,除数怎样变化,商不变?
(2)除数除以10,被除数怎样变化,商不变
(3)被除数不变,除数除以2,商会怎样变化
(除数也要乘2)
(被除数也要除以10)
(商反而乘2)
3.我来问,你来答。
回顾本节课的学习,你认为哪些内容很重要 你学会了吗
四、课堂小结
1.被除数和除数同时乘(或除以)一个相同的数 (0除外),商不变。
2.被除数不变,除数乘(或除以)几(0除外), 商反而除以(或乘)几。
3.除数不变,被除数乘(或除以)几(0除外),商也随着乘(或除以)几。
商变了
五、课后作业
完成课本“练习十七”第89页第4题、第90页第6题。
除数是两位数的除法
6
人教版·四年级上册
第10课时 商的变化规律
看谁算得又对又快?
30÷10 =
40×20=
3
800
270÷30=
9
300×5=
1500
一、新课引入
150 × 24 =
3600
15 × 24 = 360
一个因数不变,另一个因数乘(或除以)几(0除外),积也随着乘(或除以)几。
积的变化规律:
看谁算得又对又快?
问题:我们都知道乘法和除法有着密切的联系,乘法中有着像 “积的变化规律”,那在除法中是否也有规律呢?
从上往下观察,它们什么变了?什么不变?发生变化的被除数和商是怎么变化的?
(一)探索商随被除数变化而变化的规律
二、例题讲解
16
160
3200
÷ 8 =
2
20
400
× 10
除数不变
× 10
×20
× 20
× 200
× 200
除数不变,被除数乘几,商也乘几。
(一)探索商随被除数变化而变化的规律
二、例题讲解
16
160
3200
÷ 8 =
2
20
400
除数不变
除数不变,被除数除以几(0除外),商也除以几。
÷ 20
÷ 10
÷ 20
÷ 10
÷200
÷200
从下往上观察,你又能发现什么?
除数不变,
被除数乘(或除以)几(0除外),
商也随着乘(或除以)几。
被除数不变,商 除数
相同变
二、例题讲解
(一)探索商随被除数变化而变化的规律
二、例题讲解
从上往下观察,它们又什么变了?什么不变?发生变化的除数和商是怎么变化的?
(二)探索商随除数变化而变化的规律
2
20
40
200 ÷ =
100
10
5
× 10
被除数不变
× 2
÷ 10
÷ 2
× 20
÷20
被除数不变,除数乘几,商反而除以几。
二、例题讲解
从下往上观察,你又能发现什么?
(二)探索商随除数变化而变化的规律
2
20
40
200 ÷ =
100
10
5
被除数不变
被除数不变,除数除以几(0除外),商反而乘几。
÷ 2
× 2
÷ 10
× 10
÷ 20
× 20
被除数不变,
除数 乘(或除以)几(0除外),
商反而除以(或乘)几。
被除数不变,商 除数
相反变
二、例题讲解
(二)探索商随除数变化而变化的规律
6 ÷ 3 = 2
60 ÷ 30 = 2
600 ÷ 300 = 2
①
③
②
× 10
× 10
× 10
× 10
×100
× 100
被除数和除数同时乘一个相同的数,商不变。
什么变了?什么不变?
问题:从上往下观察,它们什么变了?什么不变?发生变化的被除数和除数是怎么变的?
二、例题讲解
(三)探索商不变的规律
6 ÷ 3 = 2
60 ÷ 30 = 2
600 ÷ 300 = 2
①
③
②
÷10
÷10
÷10
÷10
÷100
÷100
被除数和除数同时除以一个相同的数,商不变。
什么变了?什么不变?
问题:从下往上观察呢?你又有什么发现?
二、例题讲解
(三)探索商不变的规律
12 ÷ 3 = 4
48 ÷ 12 =
×4
×4
4
360 ÷ 30 = 12
36 ÷ ( ) = 12
÷10
÷10
3
( )
(1)
(2)
80 ÷ 40 = 2
( ) ÷ ( ) = 2
( )
( )
(3)
问题:1.第3小题要使商不变,你想让被除数和除数同时做怎样的变化?同时乘和除以一个相同的数,这个数为任何数都行吗?哪个数不行?
2.所以我们总结出的这条规律必须给它加上一个条件“0除外”。
二、例题讲解
(三)探索商不变的规律
被除数和除数同时乘(或除以)一个相同的数(0除外),商不变。
商不变的性质
二、例题讲解
(三)探索商不变的规律
1.根据每组第一题的商,写出下面两题的商。
72 ÷ 9 =
720 ÷ 90 =
7200÷900 =
3600 ÷ 40 = 90
3600 ÷ 8 =
7200 ÷ 40 =
8
8
8
450
180
三、新知运用
(1)一个除法算式,被除数乘15,要使商不变,除数也要乘15。( )
(2)如果被除数不变,除数乘4,商也随着乘4。 ( )
√
×
2.我是小判官。
(3)一个除法算式的被除数、除数都除以3以后,商是20,那么原来的商是60。 ( )
×
我来答!
(1)被除数乘2,除数怎样变化,商不变?
(2)除数除以10,被除数怎样变化,商不变
(3)被除数不变,除数除以2,商会怎样变化
(除数也要乘2)
(被除数也要除以10)
(商反而乘2)
3.我来问,你来答。
回顾本节课的学习,你认为哪些内容很重要 你学会了吗
四、课堂小结
1.被除数和除数同时乘(或除以)一个相同的数 (0除外),商不变。
2.被除数不变,除数乘(或除以)几(0除外), 商反而除以(或乘)几。
3.除数不变,被除数乘(或除以)几(0除外),商也随着乘(或除以)几。
商变了
五、课后作业
完成课本“练习十七”第89页第4题、第90页第6题。
