13.3.2等边三角形(1)课件(共23张PPT)
文档属性
| 名称 | 13.3.2等边三角形(1)课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-30 07:12:23 | ||
图片预览






文档简介
(共23张PPT)
人教版
八年级数学上
13.3.2等边三角形(1)
学习目标
1.探索等边三角形的性质和判定.(重点)
2.能运用等边三角形的性质和判定进行计算和证明.(难点)
回顾旧知
名称
图
形
定
义
性
质
判
定
等
腰
三
角
形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
合作探究
等腰三角形
等边三角形
一般三角形
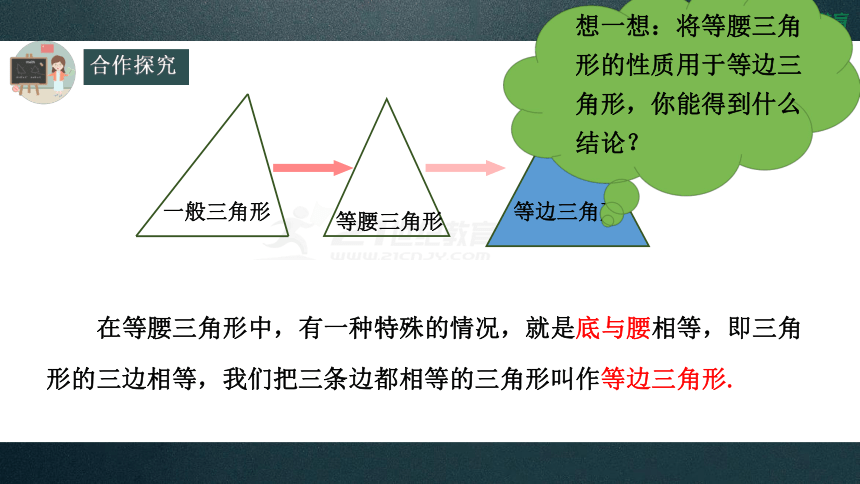
在等腰三角形中,有一种特殊的情况,就是底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫作等边三角形.
想一想:将等腰三角形的性质用于等边三角形,你能得到什么结论?
合作探究
A
B
C
A
B
C
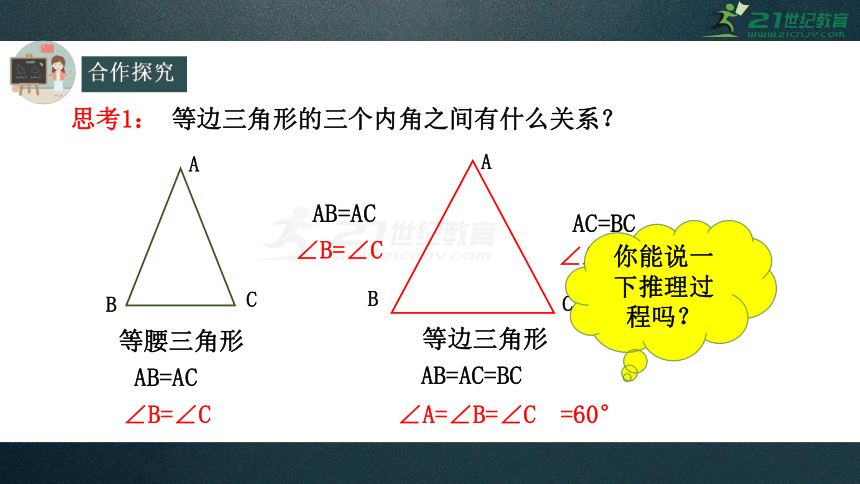
思考1:
等边三角形的三个内角之间有什么关系?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AB=AC
∠B=∠C
AC=BC
∠A=∠B
∠A=∠B=∠C
=60°
你能说一下推理过程吗?
合作探究
证明:∵ △ABC
是等边三角形,
∴ BC
=AC,BC
=AB.
∴ ∠A
=∠B,∠A
=∠C
.
∴ ∠A
=∠B
=∠C
.
∵ ∠A
+∠B
+∠C
=180°,
∴ ∠A
=60°.
∴ ∠A
=∠B
=∠C
=60°.
已知:△ABC
是等边三角形
求证:∠A
=∠B
=∠C=60°.
A
B
C
合作探究
A
B
C
A
B
C
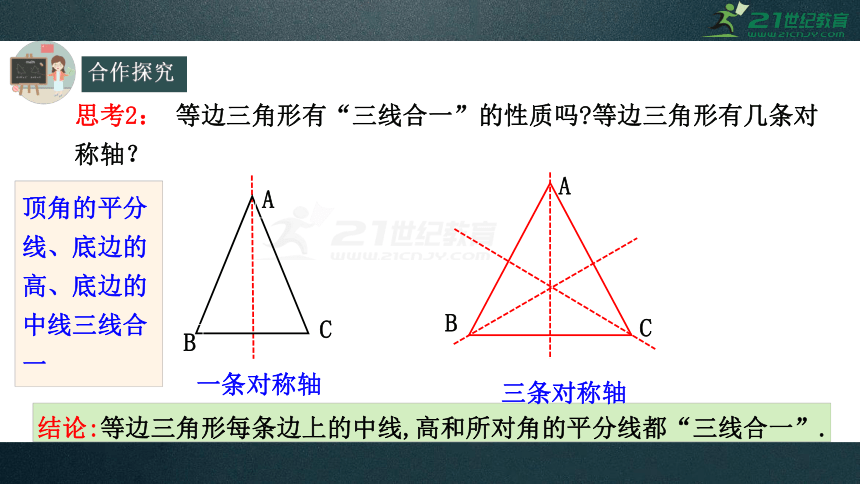
思考2:
等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高、底边的中线三线合一
一条对称轴
三条对称轴
合作探究
图形
等腰三角形
性
质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
例题精练
例1、如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,
连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
变式训练
如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
合作探究
想一想:一个三角形的三个内角满足什么条件才是等边三角形?
我们类比等腰三角形的判定来探究一下。
图形
等腰三角形
判
定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
等边三角形的判定方法:有一个角是60°的等腰三角形是等边三角形.
例题精练
例2
如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵
△ABC是等边三角形,
∴
∠A=
∠B=
∠C.
∵
DE//BC,
∴
∠ADE=
∠B,
∠
AED=
∠C.
∴
∠A=
∠ADE=
∠
AED.
∴
△ADE是等边三角形.
想一想:本题还有其他证法吗?
变式训练
若点D、E
在边AB、AC
的反向延长线上,且DE∥BC,结论依然成
立吗?
证明:
∵ △ABC
是等边三角形,
∴ ∠BAC
=∠B
=∠C
∵ DE∥BC,∴ ∠B
=∠D,∠C
=∠E.
∴ ∠EAD
=∠D
=∠E.
∴ △ADE
是等边三角形.
A
D
E
B
C
变式训练
上题中,若将条件DE∥BC改为AD=AE,
△ADE还是等边三角形吗?试说明理由.
A
C
B
D
E
证明:
∵
△ABC是等边三角形,
∴
∠A=
60°
∵
AD=AE
∴
∠ADE=
∠
AED
∴
△ADE是等边三角形.
小试牛刀
1.如图,△ABC是等边三角形,D,E,F为各边中点,
则图中等边三角形的个数是(
)
A.2
B.3
C.4
D.5
D
2.等边三角形的两条高线相交成钝角的度数是( )
A.105°
B.120°
C.135°
D.150°
B
小试牛刀
3.在等边△ABC中,BD平分∠ABC,BD=BF,则∠CDF的度数是( )
A.10°
B.15°
C.20°
D.25°
4.如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC
=2cm,则△ADE的周长是
cm.
A
C
B
D
E
12
B
小试牛刀
5、如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.
课堂小结
今天我们收获了哪些知识?
等边三角形的性质是什么?
2.你能说一说等边三角形与等腰三角形的区别和联系吗?
3.如何判定一个三角形是等边三角形呢?
综合演练
1.如图是一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是(
)
A.180°
B.220°
C.240°
D.300°
C
2.如图,已知P,Q是△ABC的BC边上的两点,BP=PQ
=QC=AP=AQ,则∠BAC的度数为______°.
120
综合演练
3.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以AB为边在△ABC外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.求证:△AEF≌△BEC.
证明:∵△ABD是等边三角形,
∴∠DAB=60°,
∵∠CAB=30°,∠ACB=90°,
∴∠EBC=180°-90°-30°=60°,
∴∠FAE=∠EBC.
∵E为AB的中点,∴AE=BE.
又∵
∠AEF=∠BEC,
∴△AEF≌△BEC(ASA).
综合演练
4、等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
解:△APQ为等边三角形.
证明如下:∵△ABC为等边三角形,∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
课后作业
教材83页习题13.3第12题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
13.3.2等边三角形(1)
学习目标
1.探索等边三角形的性质和判定.(重点)
2.能运用等边三角形的性质和判定进行计算和证明.(难点)
回顾旧知
名称
图
形
定
义
性
质
判
定
等
腰
三
角
形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
合作探究
等腰三角形
等边三角形
一般三角形
在等腰三角形中,有一种特殊的情况,就是底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫作等边三角形.
想一想:将等腰三角形的性质用于等边三角形,你能得到什么结论?
合作探究
A
B
C
A
B
C
思考1:
等边三角形的三个内角之间有什么关系?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AB=AC
∠B=∠C
AC=BC
∠A=∠B
∠A=∠B=∠C
=60°
你能说一下推理过程吗?
合作探究
证明:∵ △ABC
是等边三角形,
∴ BC
=AC,BC
=AB.
∴ ∠A
=∠B,∠A
=∠C
.
∴ ∠A
=∠B
=∠C
.
∵ ∠A
+∠B
+∠C
=180°,
∴ ∠A
=60°.
∴ ∠A
=∠B
=∠C
=60°.
已知:△ABC
是等边三角形
求证:∠A
=∠B
=∠C=60°.
A
B
C
合作探究
A
B
C
A
B
C
思考2:
等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高、底边的中线三线合一
一条对称轴
三条对称轴
合作探究
图形
等腰三角形
性
质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60?
两条边相等
三条边都相等
例题精练
例1、如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,
连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
变式训练
如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
合作探究
想一想:一个三角形的三个内角满足什么条件才是等边三角形?
我们类比等腰三角形的判定来探究一下。
图形
等腰三角形
判
定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?
等边三角形的判定方法:有一个角是60°的等腰三角形是等边三角形.
例题精练
例2
如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵
△ABC是等边三角形,
∴
∠A=
∠B=
∠C.
∵
DE//BC,
∴
∠ADE=
∠B,
∠
AED=
∠C.
∴
∠A=
∠ADE=
∠
AED.
∴
△ADE是等边三角形.
想一想:本题还有其他证法吗?
变式训练
若点D、E
在边AB、AC
的反向延长线上,且DE∥BC,结论依然成
立吗?
证明:
∵ △ABC
是等边三角形,
∴ ∠BAC
=∠B
=∠C
∵ DE∥BC,∴ ∠B
=∠D,∠C
=∠E.
∴ ∠EAD
=∠D
=∠E.
∴ △ADE
是等边三角形.
A
D
E
B
C
变式训练
上题中,若将条件DE∥BC改为AD=AE,
△ADE还是等边三角形吗?试说明理由.
A
C
B
D
E
证明:
∵
△ABC是等边三角形,
∴
∠A=
60°
∵
AD=AE
∴
∠ADE=
∠
AED
∴
△ADE是等边三角形.
小试牛刀
1.如图,△ABC是等边三角形,D,E,F为各边中点,
则图中等边三角形的个数是(
)
A.2
B.3
C.4
D.5
D
2.等边三角形的两条高线相交成钝角的度数是( )
A.105°
B.120°
C.135°
D.150°
B
小试牛刀
3.在等边△ABC中,BD平分∠ABC,BD=BF,则∠CDF的度数是( )
A.10°
B.15°
C.20°
D.25°
4.如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC
=2cm,则△ADE的周长是
cm.
A
C
B
D
E
12
B
小试牛刀
5、如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.
课堂小结
今天我们收获了哪些知识?
等边三角形的性质是什么?
2.你能说一说等边三角形与等腰三角形的区别和联系吗?
3.如何判定一个三角形是等边三角形呢?
综合演练
1.如图是一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是(
)
A.180°
B.220°
C.240°
D.300°
C
2.如图,已知P,Q是△ABC的BC边上的两点,BP=PQ
=QC=AP=AQ,则∠BAC的度数为______°.
120
综合演练
3.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以AB为边在△ABC外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.求证:△AEF≌△BEC.
证明:∵△ABD是等边三角形,
∴∠DAB=60°,
∵∠CAB=30°,∠ACB=90°,
∴∠EBC=180°-90°-30°=60°,
∴∠FAE=∠EBC.
∵E为AB的中点,∴AE=BE.
又∵
∠AEF=∠BEC,
∴△AEF≌△BEC(ASA).
综合演练
4、等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
解:△APQ为等边三角形.
证明如下:∵△ABC为等边三角形,∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
课后作业
教材83页习题13.3第12题.
https://www.21cnjy.com/help/help_extract.php
