人教版九年级上册 :24.4 弧长和扇形面积 第1课时 (共18张PPT)
文档属性
| 名称 | 人教版九年级上册 :24.4 弧长和扇形面积 第1课时 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 551.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-29 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第二十四章
圆
24.4弧长和扇形面积
第1课时
一、创设情境,揭示课题
如图,在运动会的4×100米比赛中,小明和小刚分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
因为这些弯道的
“展直长度”是一样的.
怎样来计算弯道的“展直长度”?
二、弧长的计算公式
思考:
(1)圆周长的计算公式是怎样的?
(2)圆的周长可以看做是多少度的圆心角所对的弧长?
(3)1
?的圆心角所对的弧长是多少?n
?的圆心角所对弧长是多少?
在半径为R的圆中,
n
?的圆心角所对弧长为
1.弧长公式的探求
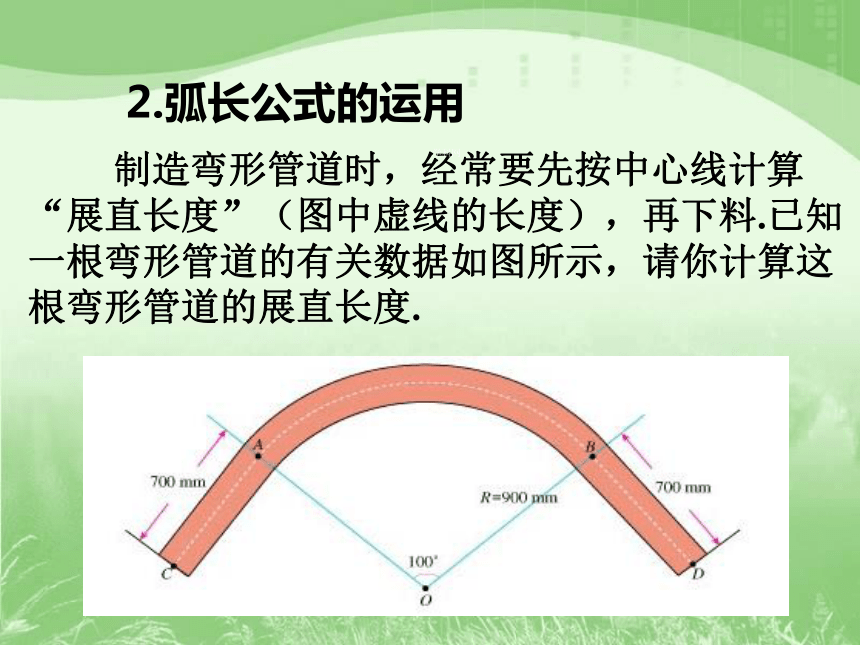
2.弧长公式的运用
制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度),再下料.已知一根弯形管道的有关数据如图所示,请你计算这根弯形管道的展直长度.
学科网
计算上图展直长度:
因此所要求的展直长度:
解后反思:
(1)弧的长短与哪几个量有关?
(2)弧长相等的两段弧是等弧吗?
圆心角、半径.
不是.
三、扇形的面积
1.扇形及扇形面积公式的探求
想一想:扇形的面积与什么有关?
讨论:怎样从圆的面积公式中找出扇形的面积与扇形的圆心角、半径之间的关系?
从而得出:半径为R,圆心角为n?的扇形的面积是
比一比:
n?的圆心角所对的弧长和扇形的面积之间有什么关系?
学科网
学科网
例2.(教科书第111页例1)
2.
扇形面积公式的应用
(1)
(1)截面上有水部分的面积是指图上哪一部分?(如图(1))
引导:
阴影部分.
D
(2)
(3)
讨论:
(2)水面高0.3
m是指哪一条线段的长(如图(2))?这条线段应该怎样画出来?
线段DC.过点O作OD垂直符号于AB并长
交圆O于C.
(3)要求图中阴影部分
面积,应该怎么办?
阴影部分面积=扇形OAB的面积-
△OAB的面积.
进一步引导:
(4)要求扇形OAB的面积,需要知道哪些量?这些量能求出来吗?
圆心角AOB的度数和半径OA的长.
(5)要求△OAB的面积,需要知道哪些量?这些量能求出来吗?
底边AB的长和高OD.
解:如图24.4-3,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵
OC=0.6,
DC=0.3,
∴
OD=OC-
DC=0.3,
∴
OD=DC.
又
AD
⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而
∠AOD=60?,
∠AOB=120?.
有水部分的面积:
S=S扇形OAB
-
S
ΔOAB
四、巩固练习
教科书第112页练习第2、3题
3.
S阴影=S
△ABC-3
S扇形AFE
五、小结提高
2.思考:如何求下列两个图中阴影部分的面积?
图(1)的阴影面积=扇形OAB的面积+
△OAB的面积
图(2)的阴影面积=扇形OAB的面积-
△OAB的面积
作业
习题24.4对应练习
第二十四章
圆
24.4弧长和扇形面积
第1课时
一、创设情境,揭示课题
如图,在运动会的4×100米比赛中,小明和小刚分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
因为这些弯道的
“展直长度”是一样的.
怎样来计算弯道的“展直长度”?
二、弧长的计算公式
思考:
(1)圆周长的计算公式是怎样的?
(2)圆的周长可以看做是多少度的圆心角所对的弧长?
(3)1
?的圆心角所对的弧长是多少?n
?的圆心角所对弧长是多少?
在半径为R的圆中,
n
?的圆心角所对弧长为
1.弧长公式的探求
2.弧长公式的运用
制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度),再下料.已知一根弯形管道的有关数据如图所示,请你计算这根弯形管道的展直长度.
学科网
计算上图展直长度:
因此所要求的展直长度:
解后反思:
(1)弧的长短与哪几个量有关?
(2)弧长相等的两段弧是等弧吗?
圆心角、半径.
不是.
三、扇形的面积
1.扇形及扇形面积公式的探求
想一想:扇形的面积与什么有关?
讨论:怎样从圆的面积公式中找出扇形的面积与扇形的圆心角、半径之间的关系?
从而得出:半径为R,圆心角为n?的扇形的面积是
比一比:
n?的圆心角所对的弧长和扇形的面积之间有什么关系?
学科网
学科网
例2.(教科书第111页例1)
2.
扇形面积公式的应用
(1)
(1)截面上有水部分的面积是指图上哪一部分?(如图(1))
引导:
阴影部分.
D
(2)
(3)
讨论:
(2)水面高0.3
m是指哪一条线段的长(如图(2))?这条线段应该怎样画出来?
线段DC.过点O作OD垂直符号于AB并长
交圆O于C.
(3)要求图中阴影部分
面积,应该怎么办?
阴影部分面积=扇形OAB的面积-
△OAB的面积.
进一步引导:
(4)要求扇形OAB的面积,需要知道哪些量?这些量能求出来吗?
圆心角AOB的度数和半径OA的长.
(5)要求△OAB的面积,需要知道哪些量?这些量能求出来吗?
底边AB的长和高OD.
解:如图24.4-3,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵
OC=0.6,
DC=0.3,
∴
OD=OC-
DC=0.3,
∴
OD=DC.
又
AD
⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而
∠AOD=60?,
∠AOB=120?.
有水部分的面积:
S=S扇形OAB
-
S
ΔOAB
四、巩固练习
教科书第112页练习第2、3题
3.
S阴影=S
△ABC-3
S扇形AFE
五、小结提高
2.思考:如何求下列两个图中阴影部分的面积?
图(1)的阴影面积=扇形OAB的面积+
△OAB的面积
图(2)的阴影面积=扇形OAB的面积-
△OAB的面积
作业
习题24.4对应练习
同课章节目录
