同底数幂的乘法
图片预览

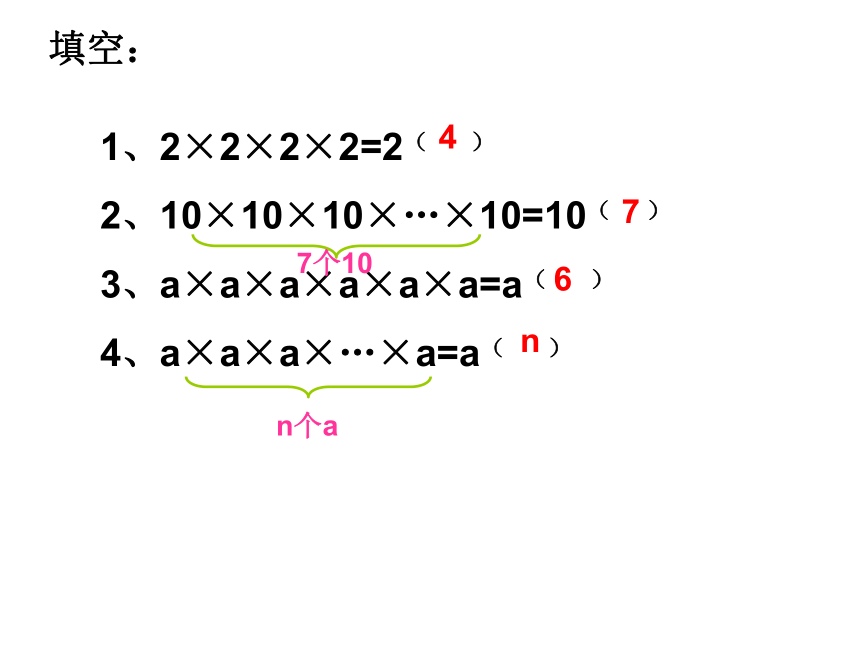





文档简介
(共25张PPT)
欢迎您走进我们的课堂
中川乡中心学校
郭忠花
2010、12、10
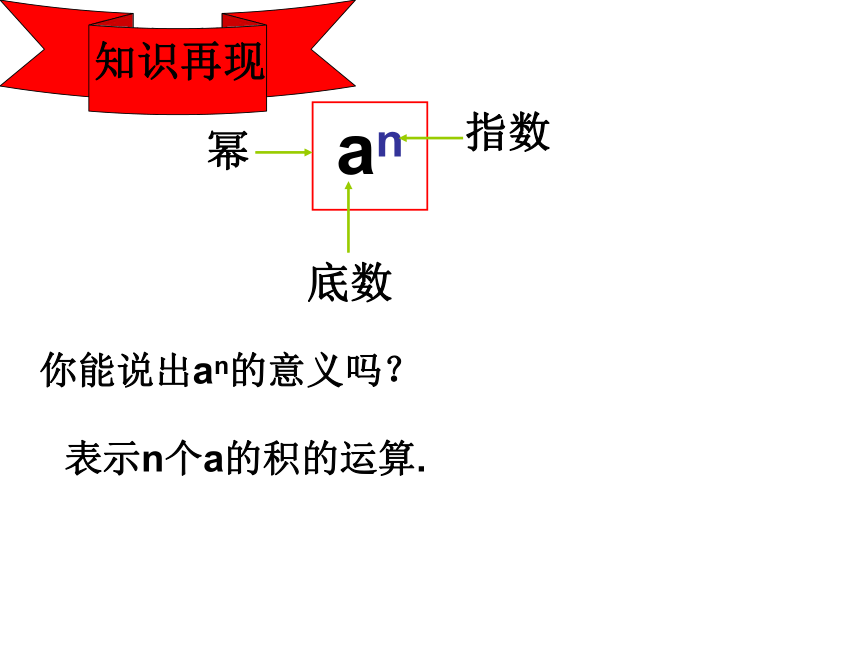
an
底数
指数
幂
知识再现
你能说出an的意义吗?
表示n个a的积的运算.
填空:
1、2×2×2×2=2( )
2、10×10×10×…×10=10( )
3、a×a×a×a×a×a=a( )
4、a×a×a×…×a=a( )
7个10
n个a
4
7
6
n
情境创设:
数的世界充满着神奇,
幂的运算方便了 数的处理!
一个长方体的长、宽、高分别是107㎝,
106㎝,103㎝,则它的体积是多少㎝3
大
试一试:
5
2
10
2
5
10
×
2
(4)
(1)
(2)
(3)
3
=
3
×
5
=
2
8
5
7
×
=
2
5
10
9
a
a
a
5
3
2
=
2
3
自己做学习的主人
33×32=(3×3×3) ×(3×3)
表示5个3相乘
=35
请观察这一组运算,你能从中发现什么
如何计算:33×32
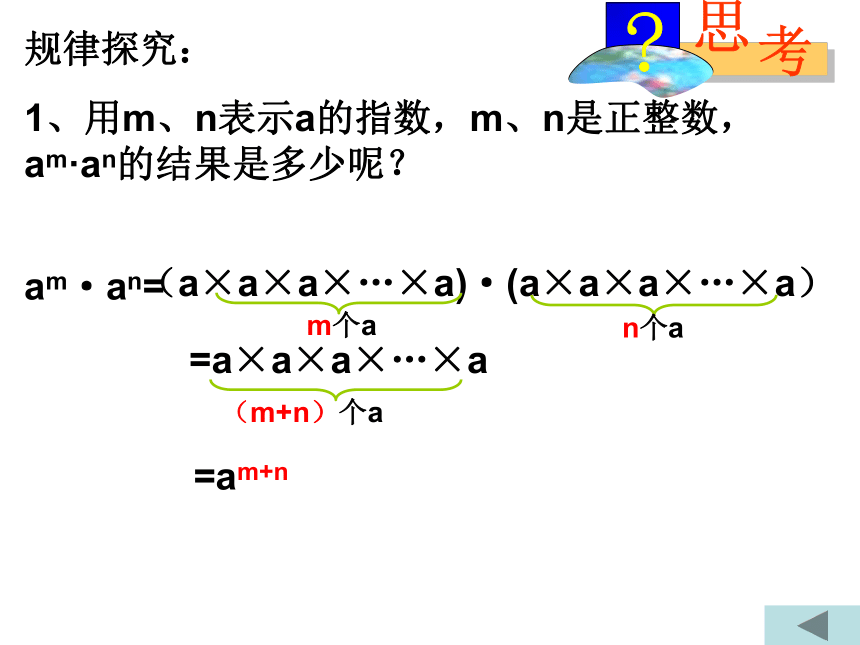
规律探究:
1、用m、n表示a的指数,m、n是正整数,am·an的结果是多少呢?
am·an=
(a×a×a×…×a)·(a×a×a×…×a)
m个a
n个a
=a×a×a×…×a
(m+n)个a
=am+n
结论:
am·an=am+n(m、n都是正整数)
你能用文字语言将同底数幂乘法的性质叙述出来吗?
同底数幂相乘,底数 ,指数 .
请你推广:
am·an·as=
am+n+s
(m、n、s都是正整数)
运用同底数幂的乘法性质的条件:
1、判断是同底数幂
2、是乘法
不变
相加
计算
(1) a a6 (2) - x2·x7
2×24×23 (3) xm x3m+1
指数是1不要漏了
解(1)原式=a1+6=a7
(2)原式=-x2+7=-x9
(3)原式=21+4+3=28
(4)原式=xm+3m+1=x4m+1
幻灯片 4
计算
(1) b5 b
(2) 10×102×103
(3) -a2 a6
(4) y2n yn+1
巩固练习
b6
106
-a8
y3n+1
巩固练习
下列计算是否正确
(1)a2+a3=2a5 (2)a2·a3=a5
(3)a2·a3=a6 (4)a2+a3=a5
(5)a2+a2=a4 (6)xm+xm=2xm
x
√
x
x
x
√
计算:
1. (-2)2 ; (-2)3 ; (-a)4 ;
2. (-b)5 ; (-3)4 ; (-3)5 ;
3. (-1)2 ; (-1)3 ; (-1)2m; (-1)2m+1
(m是正整数)
拓展延伸 计算 (-8)5× (-8)12
美 好 的 回 忆
……
今天,我们学到了什么?
同底数幂相乘,底数不变,指数相加。
运用同底数幂的乘法性质的条件:
1、判断是同底数幂
2、是乘法
欢迎您走进我们的课堂
你能用文字语言将
同底数幂乘法的性质叙述出来吗?
am·an=am+n
(m、n都是正整数)
同底数幂相乘,
底数 不变,指数相加. .
判断:
a2+a2=a4
a2+a3=a5
xm+xm=2xm
xmxm=2xm
3m+2m=5m
同底数的幂的乘法
与合并同类项有什么区别
例题:计算
x2·x5+x3·x4
练习:计算
1、y4·y-y·y·y3
2、2×24+22×23
3、a2·a·a5+a3·a2·a3
(5) (-y)2n+1·(-y)3 (n是正整数)
(1) (-a) ·(-a)3
(2) (-a4) ·(-a3)
(3) (-a)4·(-a3)
(4) -t(-t)2-t3
计算
根据幂的符号规律,可把不同底数的幂
化成同底数的幂相乘.
例题:计算
1、x2·x5+x3·x4
2、(x+y)2·(x+y)3
练习:计算
1、y4·y-y·y·y3
2、(x-y)3·(x-y)2·(x-y)
3 23×4×8×16(结果用幂的形式表示)
4、103×100×10+100×100×100
3、 3×9×27×81
4、105×10+100×100×102
5、2×24+22×23
例题:填空
a3·a( )=a8
(2)a4·_____·a2=a10
(3)若a4·am=a10,则m=____
(4)若xm·xm=x8,则m=____
(5)若x·xa·x4=x2a+3,则a=____.
(6)a2n·a( )=an+2·a( )=a2n+2=a( ) ·an+1
5
a4
6
4
2
试一试:
已知am=8,an=32,求am+n的值.
2
n
n+1
计算 (x-y)2(y-x)3
计算
(a-b)2(a-b)3(b-a)4
(m-n)(n-m)4(m-n)3
(s-t)m(s-t)m+n(t-s)
(x-y)m(y-x)m+1(y-x)
通过这节课的学习:
我最大的收获是______________
我对自己的表现评价如何_____________
我从同学身上学到了________________
总
结
与
回
顾
欢迎您走进我们的课堂
中川乡中心学校
郭忠花
2010、12、10
an
底数
指数
幂
知识再现
你能说出an的意义吗?
表示n个a的积的运算.
填空:
1、2×2×2×2=2( )
2、10×10×10×…×10=10( )
3、a×a×a×a×a×a=a( )
4、a×a×a×…×a=a( )
7个10
n个a
4
7
6
n
情境创设:
数的世界充满着神奇,
幂的运算方便了 数的处理!
一个长方体的长、宽、高分别是107㎝,
106㎝,103㎝,则它的体积是多少㎝3
大
试一试:
5
2
10
2
5
10
×
2
(4)
(1)
(2)
(3)
3
=
3
×
5
=
2
8
5
7
×
=
2
5
10
9
a
a
a
5
3
2
=
2
3
自己做学习的主人
33×32=(3×3×3) ×(3×3)
表示5个3相乘
=35
请观察这一组运算,你能从中发现什么
如何计算:33×32
规律探究:
1、用m、n表示a的指数,m、n是正整数,am·an的结果是多少呢?
am·an=
(a×a×a×…×a)·(a×a×a×…×a)
m个a
n个a
=a×a×a×…×a
(m+n)个a
=am+n
结论:
am·an=am+n(m、n都是正整数)
你能用文字语言将同底数幂乘法的性质叙述出来吗?
同底数幂相乘,底数 ,指数 .
请你推广:
am·an·as=
am+n+s
(m、n、s都是正整数)
运用同底数幂的乘法性质的条件:
1、判断是同底数幂
2、是乘法
不变
相加
计算
(1) a a6 (2) - x2·x7
2×24×23 (3) xm x3m+1
指数是1不要漏了
解(1)原式=a1+6=a7
(2)原式=-x2+7=-x9
(3)原式=21+4+3=28
(4)原式=xm+3m+1=x4m+1
幻灯片 4
计算
(1) b5 b
(2) 10×102×103
(3) -a2 a6
(4) y2n yn+1
巩固练习
b6
106
-a8
y3n+1
巩固练习
下列计算是否正确
(1)a2+a3=2a5 (2)a2·a3=a5
(3)a2·a3=a6 (4)a2+a3=a5
(5)a2+a2=a4 (6)xm+xm=2xm
x
√
x
x
x
√
计算:
1. (-2)2 ; (-2)3 ; (-a)4 ;
2. (-b)5 ; (-3)4 ; (-3)5 ;
3. (-1)2 ; (-1)3 ; (-1)2m; (-1)2m+1
(m是正整数)
拓展延伸 计算 (-8)5× (-8)12
美 好 的 回 忆
……
今天,我们学到了什么?
同底数幂相乘,底数不变,指数相加。
运用同底数幂的乘法性质的条件:
1、判断是同底数幂
2、是乘法
欢迎您走进我们的课堂
你能用文字语言将
同底数幂乘法的性质叙述出来吗?
am·an=am+n
(m、n都是正整数)
同底数幂相乘,
底数 不变,指数相加. .
判断:
a2+a2=a4
a2+a3=a5
xm+xm=2xm
xmxm=2xm
3m+2m=5m
同底数的幂的乘法
与合并同类项有什么区别
例题:计算
x2·x5+x3·x4
练习:计算
1、y4·y-y·y·y3
2、2×24+22×23
3、a2·a·a5+a3·a2·a3
(5) (-y)2n+1·(-y)3 (n是正整数)
(1) (-a) ·(-a)3
(2) (-a4) ·(-a3)
(3) (-a)4·(-a3)
(4) -t(-t)2-t3
计算
根据幂的符号规律,可把不同底数的幂
化成同底数的幂相乘.
例题:计算
1、x2·x5+x3·x4
2、(x+y)2·(x+y)3
练习:计算
1、y4·y-y·y·y3
2、(x-y)3·(x-y)2·(x-y)
3 23×4×8×16(结果用幂的形式表示)
4、103×100×10+100×100×100
3、 3×9×27×81
4、105×10+100×100×102
5、2×24+22×23
例题:填空
a3·a( )=a8
(2)a4·_____·a2=a10
(3)若a4·am=a10,则m=____
(4)若xm·xm=x8,则m=____
(5)若x·xa·x4=x2a+3,则a=____.
(6)a2n·a( )=an+2·a( )=a2n+2=a( ) ·an+1
5
a4
6
4
2
试一试:
已知am=8,an=32,求am+n的值.
2
n
n+1
计算 (x-y)2(y-x)3
计算
(a-b)2(a-b)3(b-a)4
(m-n)(n-m)4(m-n)3
(s-t)m(s-t)m+n(t-s)
(x-y)m(y-x)m+1(y-x)
通过这节课的学习:
我最大的收获是______________
我对自己的表现评价如何_____________
我从同学身上学到了________________
总
结
与
回
顾
