1.3.1 有理数的加法课件(共16张PPT)
文档属性
| 名称 | 1.3.1 有理数的加法课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-30 16:27:05 | ||
图片预览





文档简介
(共16张PPT)
1.3.1
有理数的加法
人教版
七年级
教学目标:
1.理解有理数加法法则;
2.利用加法法则正确地进行有理数的加法运算.
3.用数形结合的思想方法得出有理数加法法则.
重点、难点
重点:熟练应用有理数的加法法则进行加法运算.
难点:有理数的加法法则的理解.
复习回顾,引入新课
有理数有几种分类方法?都是如何分类的呢?
(1)按定义分类:
有理数分成整数,分数;整数又分成正整数,负整数和0;分数分成正分数和负分数。
(2)按性质分类:
有理数分成正数,0,负数;正数又分成正整数和正分数,负数分成负整数和负分数。
在小学,我们学过正数及0的加法运算.学过的加法类型是正数与正数相加、正数与0相加.引入负数后,加法的类型还有哪几种呢?
结论:共三种类型.
即:
(1)同号两个数相加;
(2)异号两个数相加;
(3)一个数与0相加.
正数+正数
0+正数
负数+正数
0+0
负数+0
0+负数
负数+负数
第一个加数
第二个加数
正数
0
负数
正数
0
负数
正数+0
负数+负数
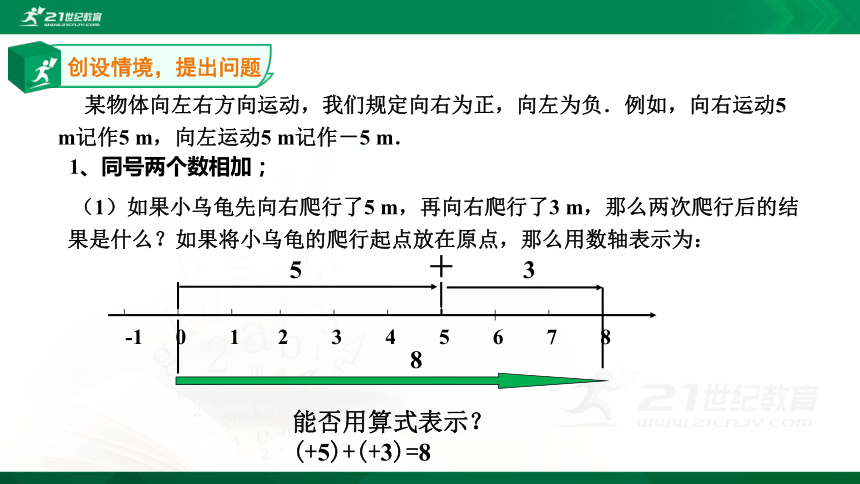
某物体向左右方向运动,我们规定向右为正,向左为负.例如,向右运动5
m记作5
m,向左运动5
m记作-5
m.
(1)如果小乌龟先向右爬行了5
m,再向右爬行了3
m,那么两次爬行后的结果是什么?如果将小乌龟的爬行起点放在原点,那么用数轴表示为:
能否用算式表示?
(+5)+(+3)=8
-1
0
1
2
3
4
5
6
7
8
5
3
+
8
创设情境,提出问题
1、同号两个数相加;
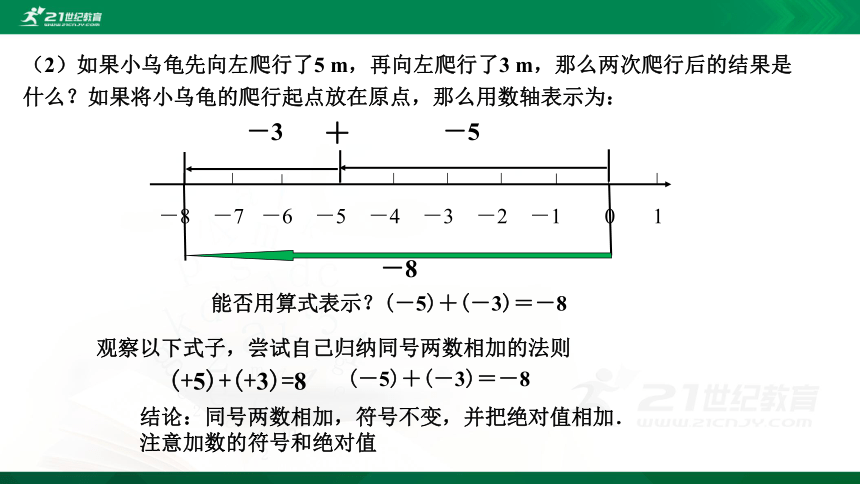
(2)如果小乌龟先向左爬行了5
m,再向左爬行了3
m,那么两次爬行后的结果是什么?如果将小乌龟的爬行起点放在原点,那么用数轴表示为:
能否用算式表示?(-5)+(-3)=-8
-3
-5
+
-8
-8
-7
-6
-5
-4
-3
-2
-1
0
1
(-5)+(-3)=-8
(+5)+(+3)=8
观察以下式子,尝试自己归纳同号两数相加的法则
结论:同号两数相加,符号不变,并把绝对值相加.
注意加数的符号和绝对值
求以下小乌龟两次爬行后的结果,并用算式表示:
(1)先向左爬行了6m,再向右爬行了8m,
小乌龟从起点向
爬行了
m,
;
(2)先向右爬行了6m,再向左爬行了8
m,
小乌龟从起点向
爬行了
m
,
;
(3)先向左爬行了8m,再向右爬行了8
m,
小乌龟从起点爬行了
m
,
.
0
右
左
2
2
(-6)+8=
2
6+(-8)=-2
(-8)+8=
0
观察以上式子,尝试自己归纳异号两数相加的法则
结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0
.
2、异号两个数相加;
如果小乌龟第1
s向左(或右)爬行了5
m,第2秒原地不动,很显然,两秒后小乌龟从起点向左(或右)爬行了5
m.如何用算式表示呢?
(-5)+0=-5
或
5+0=5.
结论:一个数0相加,仍得这个数.
注意:有理数加法运算时,需先定号再计算。
3、一个数与0相加.
观察以上式子,尝试自己归纳一个数与0相加的法则
拓展延伸
观察下列式子所得结果,能得出什么结论?
(1)30+(-20)=10,(-20)+30=10
(2)20+30=50,30+20=50
(3)(-20)+(-30)=-50,(-30)+(-20)=-50
(4)[8+(-5)]+(-4)=-1,8+[(-5)+(-4)]=-1
(5)
[8+5]+(-4)=9,8+[5+(-4)]=9
(6)[(-8)+(-5)]+(-4)=-17,(-8)+[(-5)+(-4)]=-17
(7)[8+5]+4=17,
8+[5+4]=17
结论:(1)有理数的加法中,两个数相加,交换加数的位置,和不变。
加法交换律:a+b=b+a
(2)有理数的加法中,三个数相加,先把前面两个数相加,或者想把后两个数相加,和不变。
加法结合律(a+b)+c=a+(b+c)
例题讲解
例1
(1)(-3)+(-9);
解:原式=-(3+9)=-12
(2)(-4.7)+3.9;
解:原式=
-(4.7-3.9)=-0.8
例2
计算16+(-25)+24+(-35)
解:原式=
16+24+[(-25)+(-35)]=40+
(-60)=-20
利用加法交换律、结合律可使运算简化。
课堂练习
1.气温由﹣5℃上升了4℃时的气温是(
A
)
A.﹣1℃
B.1℃
C.﹣9℃
D.9℃
解:根据题意得:﹣5+4=﹣1,
则气温由﹣5℃上升了4℃时的气温是﹣1℃.
2.比﹣3大5的数是(
B
)
A.8
B.2
C.﹣8
D.﹣2
解:﹣3+5=2.
3.下列说法中,正确的有(
B
)
①0是最小的整数;②若|a|=|b|,则a=b;
③互为相反数的两数之和为零;
④数轴上表示两个有理数的点,较大的数表示的点离原点较远.
A.0个
B.1个
C.2个
D.3个
解:①0是最小的整数,错误,没有最小的整数;
②若|a|=|b|,则a=±b,故此选项错误;
③互为相反数的两数之和为零,正确;
④数轴上表示两个有理数的点,较大的数表示的点离原点较远,只有都是正数时较大的数表示的点离原点较远,故此选项错误.
4.
计算:﹣(﹣3)+|﹣5|
解:﹣(﹣3)+|﹣5|=3+5=8.
5.若a+b+c=0且a>b>c,则下列几个数中:①a+b;②ab;③ab2;
④b2﹣ac;
⑤﹣(b+c),一定是正数的有 ①④⑤
解:∵a+b+c=0且a>b>c,∴a>0,c<0,b可以是正数,负数或0,
∴①a+b=﹣c>0,②ab可以为正数,负数或0,③ab2可以是正数或0,
④ac<0,∴b2﹣ac>0,⑤﹣(b+c)=a>0.
6.已知:﹣a=2,|b|=6,且a>b,则a+b的值。
解:∵﹣a=2,|b|=6,且a>b,
∴a=﹣2,b=﹣6,
∴a+b=﹣2+(﹣6)=﹣8,
课堂小结
1、有理数加法法则:
(1)同号两数相加,取相同符号,并把绝对值相加.
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
2、先定符号,再算绝对值.
3、加法交换律:a+b=b+a.
加法结合律(a+b)+c=a+(b+c)
4、使用了数形结合的数学研究方法总结加法法则.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.3.1
有理数的加法
人教版
七年级
教学目标:
1.理解有理数加法法则;
2.利用加法法则正确地进行有理数的加法运算.
3.用数形结合的思想方法得出有理数加法法则.
重点、难点
重点:熟练应用有理数的加法法则进行加法运算.
难点:有理数的加法法则的理解.
复习回顾,引入新课
有理数有几种分类方法?都是如何分类的呢?
(1)按定义分类:
有理数分成整数,分数;整数又分成正整数,负整数和0;分数分成正分数和负分数。
(2)按性质分类:
有理数分成正数,0,负数;正数又分成正整数和正分数,负数分成负整数和负分数。
在小学,我们学过正数及0的加法运算.学过的加法类型是正数与正数相加、正数与0相加.引入负数后,加法的类型还有哪几种呢?
结论:共三种类型.
即:
(1)同号两个数相加;
(2)异号两个数相加;
(3)一个数与0相加.
正数+正数
0+正数
负数+正数
0+0
负数+0
0+负数
负数+负数
第一个加数
第二个加数
正数
0
负数
正数
0
负数
正数+0
负数+负数
某物体向左右方向运动,我们规定向右为正,向左为负.例如,向右运动5
m记作5
m,向左运动5
m记作-5
m.
(1)如果小乌龟先向右爬行了5
m,再向右爬行了3
m,那么两次爬行后的结果是什么?如果将小乌龟的爬行起点放在原点,那么用数轴表示为:
能否用算式表示?
(+5)+(+3)=8
-1
0
1
2
3
4
5
6
7
8
5
3
+
8
创设情境,提出问题
1、同号两个数相加;
(2)如果小乌龟先向左爬行了5
m,再向左爬行了3
m,那么两次爬行后的结果是什么?如果将小乌龟的爬行起点放在原点,那么用数轴表示为:
能否用算式表示?(-5)+(-3)=-8
-3
-5
+
-8
-8
-7
-6
-5
-4
-3
-2
-1
0
1
(-5)+(-3)=-8
(+5)+(+3)=8
观察以下式子,尝试自己归纳同号两数相加的法则
结论:同号两数相加,符号不变,并把绝对值相加.
注意加数的符号和绝对值
求以下小乌龟两次爬行后的结果,并用算式表示:
(1)先向左爬行了6m,再向右爬行了8m,
小乌龟从起点向
爬行了
m,
;
(2)先向右爬行了6m,再向左爬行了8
m,
小乌龟从起点向
爬行了
m
,
;
(3)先向左爬行了8m,再向右爬行了8
m,
小乌龟从起点爬行了
m
,
.
0
右
左
2
2
(-6)+8=
2
6+(-8)=-2
(-8)+8=
0
观察以上式子,尝试自己归纳异号两数相加的法则
结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0
.
2、异号两个数相加;
如果小乌龟第1
s向左(或右)爬行了5
m,第2秒原地不动,很显然,两秒后小乌龟从起点向左(或右)爬行了5
m.如何用算式表示呢?
(-5)+0=-5
或
5+0=5.
结论:一个数0相加,仍得这个数.
注意:有理数加法运算时,需先定号再计算。
3、一个数与0相加.
观察以上式子,尝试自己归纳一个数与0相加的法则
拓展延伸
观察下列式子所得结果,能得出什么结论?
(1)30+(-20)=10,(-20)+30=10
(2)20+30=50,30+20=50
(3)(-20)+(-30)=-50,(-30)+(-20)=-50
(4)[8+(-5)]+(-4)=-1,8+[(-5)+(-4)]=-1
(5)
[8+5]+(-4)=9,8+[5+(-4)]=9
(6)[(-8)+(-5)]+(-4)=-17,(-8)+[(-5)+(-4)]=-17
(7)[8+5]+4=17,
8+[5+4]=17
结论:(1)有理数的加法中,两个数相加,交换加数的位置,和不变。
加法交换律:a+b=b+a
(2)有理数的加法中,三个数相加,先把前面两个数相加,或者想把后两个数相加,和不变。
加法结合律(a+b)+c=a+(b+c)
例题讲解
例1
(1)(-3)+(-9);
解:原式=-(3+9)=-12
(2)(-4.7)+3.9;
解:原式=
-(4.7-3.9)=-0.8
例2
计算16+(-25)+24+(-35)
解:原式=
16+24+[(-25)+(-35)]=40+
(-60)=-20
利用加法交换律、结合律可使运算简化。
课堂练习
1.气温由﹣5℃上升了4℃时的气温是(
A
)
A.﹣1℃
B.1℃
C.﹣9℃
D.9℃
解:根据题意得:﹣5+4=﹣1,
则气温由﹣5℃上升了4℃时的气温是﹣1℃.
2.比﹣3大5的数是(
B
)
A.8
B.2
C.﹣8
D.﹣2
解:﹣3+5=2.
3.下列说法中,正确的有(
B
)
①0是最小的整数;②若|a|=|b|,则a=b;
③互为相反数的两数之和为零;
④数轴上表示两个有理数的点,较大的数表示的点离原点较远.
A.0个
B.1个
C.2个
D.3个
解:①0是最小的整数,错误,没有最小的整数;
②若|a|=|b|,则a=±b,故此选项错误;
③互为相反数的两数之和为零,正确;
④数轴上表示两个有理数的点,较大的数表示的点离原点较远,只有都是正数时较大的数表示的点离原点较远,故此选项错误.
4.
计算:﹣(﹣3)+|﹣5|
解:﹣(﹣3)+|﹣5|=3+5=8.
5.若a+b+c=0且a>b>c,则下列几个数中:①a+b;②ab;③ab2;
④b2﹣ac;
⑤﹣(b+c),一定是正数的有 ①④⑤
解:∵a+b+c=0且a>b>c,∴a>0,c<0,b可以是正数,负数或0,
∴①a+b=﹣c>0,②ab可以为正数,负数或0,③ab2可以是正数或0,
④ac<0,∴b2﹣ac>0,⑤﹣(b+c)=a>0.
6.已知:﹣a=2,|b|=6,且a>b,则a+b的值。
解:∵﹣a=2,|b|=6,且a>b,
∴a=﹣2,b=﹣6,
∴a+b=﹣2+(﹣6)=﹣8,
课堂小结
1、有理数加法法则:
(1)同号两数相加,取相同符号,并把绝对值相加.
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
2、先定符号,再算绝对值.
3、加法交换律:a+b=b+a.
加法结合律(a+b)+c=a+(b+c)
4、使用了数形结合的数学研究方法总结加法法则.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
