人教版数学五年级上册 多边形的面积 复习提升 课件(14页ppt)
文档属性
| 名称 | 人教版数学五年级上册 多边形的面积 复习提升 课件(14页ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 804.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-30 11:11:54 | ||
图片预览




文档简介
多边形的面积
6
人教版·五年级上册
第六单元复习提升
一、学习目标
1.通过整理和复习,进一步理解和掌握多边形面积计算公式,能正确、灵活地运用公式进行有关计算,解决一些简单的实际问题。
2.通过操作、观察、比较,发展学生的空间观念,建立良好的知识结构,培养创新意识。
3.通过对平面图形面积公式之间的关系研究,强化转化的数学思想。
二、学习重难点
学习重点:
熟练计算平行四边形、三角形、梯形及组合图形的面积。
学习难点:
明确各种图形面积的推导过程,理清图形面积之间的关系。
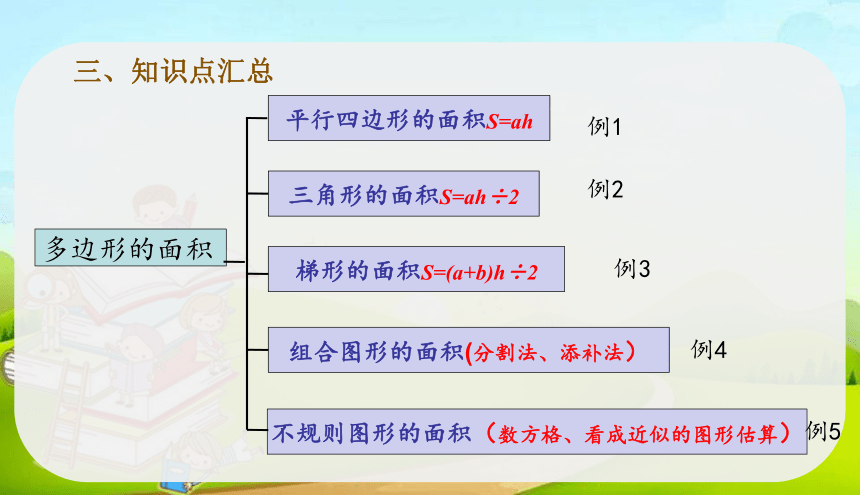
三、知识点汇总
多边形的面积
平行四边形的面积S=ah
三角形的面积S=ah÷2
梯形的面积S=(a+b)h÷2
组合图形的面积(分割法、添补法)
不规则图形的面积(数方格、看成近似的图形估算)
例1
例2
例5
例3
例4
四、问题解决
a
b
a
h
a
h
a
b
h
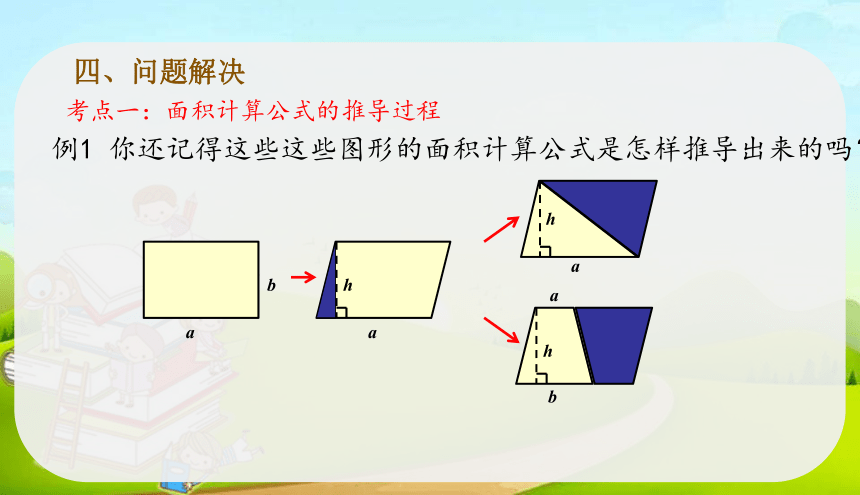
例1 你还记得这些这些图形的面积计算公式是怎样推导出来的吗?
考点一:面积计算公式的推导过程
四、问题解决
(1)说一说:平行四边形、三角形和梯形面积计算公式的推导都用到了什么方法?
b
h
a
转化的方法。
b
h
a
(2)试一试:延长或缩短梯形的上底,看看你又能发现点什么。
我发现,当梯形的上底和下底相等时就成了平行四边形;当梯形的上底为0时就成了三角形。
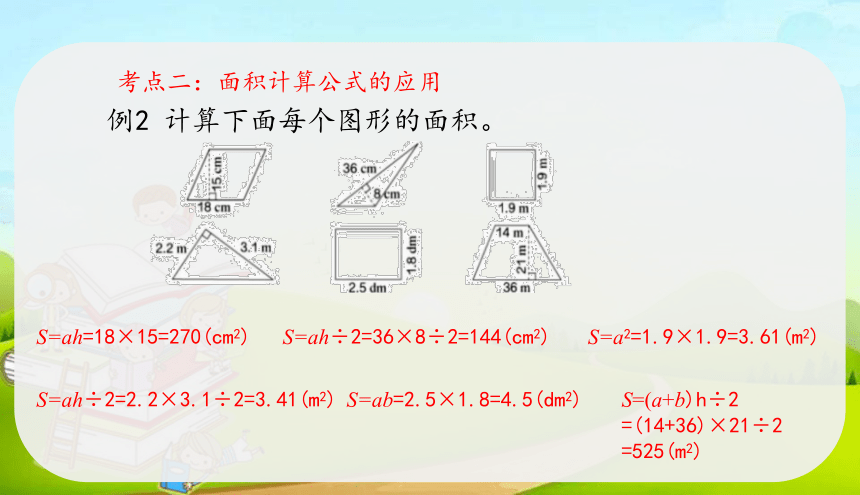
例2 计算下面每个图形的面积。
S=ah=18×15=270(cm2)
S=ah÷2=36×8÷2=144(cm2)
S=a2=1.9×1.9=3.61(m2)
S=ah÷2=2.2×3.1÷2=3.41(m2)
S=ab=2.5×1.8=4.5(dm2)
S=(a+b)h÷2
=(14+36)×21÷2
=525(m2)
考点二:面积计算公式的应用
四、问题解决
方法一:
5×12+(10-5)×(12-6)÷2
=75(cm?)
方法二:
(5+10)×(12-6)÷2+6×5
=75(cm?)
例3 计算右面图形的面积。你能想出几种方法?
考点三:组合图形的面积
五、复习提升
1.填一填。
(1)两个完全一样的三角形一定能拼成一个( )形。
(2)一个梯形的上底与下底的和是20厘米,高是5厘米,面积是( )平方厘米。
(3)一个三角形的面积是4.5平方米,底边上的高是1.5米,底是( )米。
(4)一个三角形的面积是2.5平方米,与它等底等高的平行四边形的面积是( )平方米。
平行四边
50
6
5
五、复习提升
2.判断题。
(1)平行四边形的面积一定比梯形的面积大 。 ( )
(2)两个面积相等的三角形一定能拼成一个平行四边形。( )
(3)梯形的上底、下底越长,面积越大。 ( )
(4)任何一个梯形都可以分成两个等高的三角形。 ( )
×
×
×
√
五、复习提升
3.右图是教室的一面墙。如果砌这面墙平均每平方米用砖185块,一共需要用多少块砖?(教材P104第3题)
5×4+5×1.2÷2=23(平方米)
185×23=4255(块)
答:一共需要用4255块砖。
六、拓展提升
60
40
求阴影部分的面积。(单位:厘米)
60×60+40×40=5200(平方厘米)
(60+40)×60÷2=3000(平方厘米)
5200-3000=2200(平方厘米)
七、课后作业
完成课本“练习二十三”第104页第2题、第4题、第5题。
聪明出于勤奋,天才在于积累。
6
人教版·五年级上册
第六单元复习提升
一、学习目标
1.通过整理和复习,进一步理解和掌握多边形面积计算公式,能正确、灵活地运用公式进行有关计算,解决一些简单的实际问题。
2.通过操作、观察、比较,发展学生的空间观念,建立良好的知识结构,培养创新意识。
3.通过对平面图形面积公式之间的关系研究,强化转化的数学思想。
二、学习重难点
学习重点:
熟练计算平行四边形、三角形、梯形及组合图形的面积。
学习难点:
明确各种图形面积的推导过程,理清图形面积之间的关系。
三、知识点汇总
多边形的面积
平行四边形的面积S=ah
三角形的面积S=ah÷2
梯形的面积S=(a+b)h÷2
组合图形的面积(分割法、添补法)
不规则图形的面积(数方格、看成近似的图形估算)
例1
例2
例5
例3
例4
四、问题解决
a
b
a
h
a
h
a
b
h
例1 你还记得这些这些图形的面积计算公式是怎样推导出来的吗?
考点一:面积计算公式的推导过程
四、问题解决
(1)说一说:平行四边形、三角形和梯形面积计算公式的推导都用到了什么方法?
b
h
a
转化的方法。
b
h
a
(2)试一试:延长或缩短梯形的上底,看看你又能发现点什么。
我发现,当梯形的上底和下底相等时就成了平行四边形;当梯形的上底为0时就成了三角形。
例2 计算下面每个图形的面积。
S=ah=18×15=270(cm2)
S=ah÷2=36×8÷2=144(cm2)
S=a2=1.9×1.9=3.61(m2)
S=ah÷2=2.2×3.1÷2=3.41(m2)
S=ab=2.5×1.8=4.5(dm2)
S=(a+b)h÷2
=(14+36)×21÷2
=525(m2)
考点二:面积计算公式的应用
四、问题解决
方法一:
5×12+(10-5)×(12-6)÷2
=75(cm?)
方法二:
(5+10)×(12-6)÷2+6×5
=75(cm?)
例3 计算右面图形的面积。你能想出几种方法?
考点三:组合图形的面积
五、复习提升
1.填一填。
(1)两个完全一样的三角形一定能拼成一个( )形。
(2)一个梯形的上底与下底的和是20厘米,高是5厘米,面积是( )平方厘米。
(3)一个三角形的面积是4.5平方米,底边上的高是1.5米,底是( )米。
(4)一个三角形的面积是2.5平方米,与它等底等高的平行四边形的面积是( )平方米。
平行四边
50
6
5
五、复习提升
2.判断题。
(1)平行四边形的面积一定比梯形的面积大 。 ( )
(2)两个面积相等的三角形一定能拼成一个平行四边形。( )
(3)梯形的上底、下底越长,面积越大。 ( )
(4)任何一个梯形都可以分成两个等高的三角形。 ( )
×
×
×
√
五、复习提升
3.右图是教室的一面墙。如果砌这面墙平均每平方米用砖185块,一共需要用多少块砖?(教材P104第3题)
5×4+5×1.2÷2=23(平方米)
185×23=4255(块)
答:一共需要用4255块砖。
六、拓展提升
60
40
求阴影部分的面积。(单位:厘米)
60×60+40×40=5200(平方厘米)
(60+40)×60÷2=3000(平方厘米)
5200-3000=2200(平方厘米)
七、课后作业
完成课本“练习二十三”第104页第2题、第4题、第5题。
聪明出于勤奋,天才在于积累。
