六年级上册数学课件-5.2 圆的周长 人教版(85张ppt)
文档属性
| 名称 | 六年级上册数学课件-5.2 圆的周长 人教版(85张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-30 21:33:59 | ||
图片预览










文档简介
圆 的 周 长
九年义务教育小学六年级数学上册
学习目标:
1. 知道什么是圆的周长。
2. 理解并掌握圆周率的意义和近似值。
3 .初步理解和掌握圆的周长计算公式,能正确计算圆的周长。
4 .通过了解祖冲之在圆周率方面所作的贡献,渗透爱国主义思想。
学习重点:
???????理解和掌握圆的周长的计算公式。
学习难点:
??? ???对圆周率的认识。
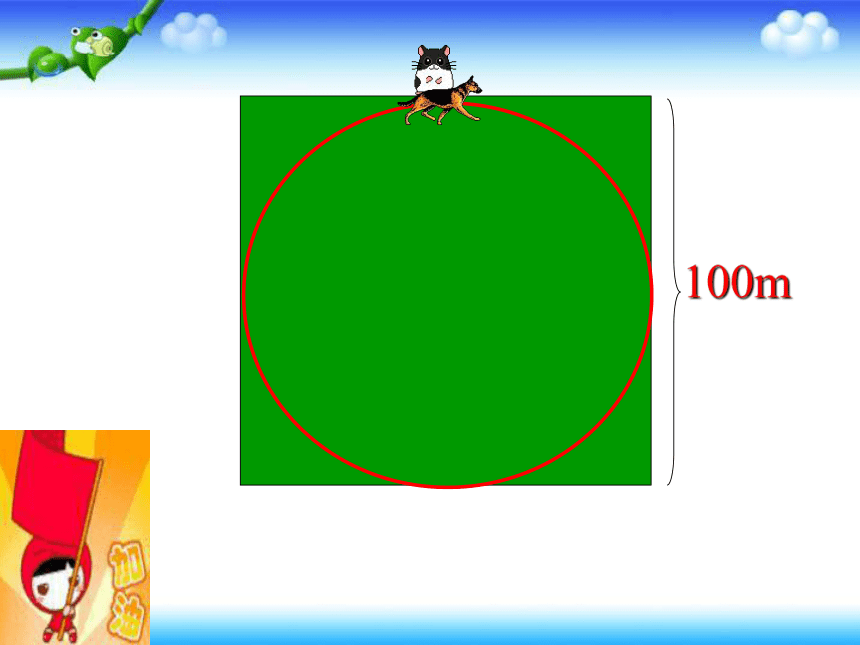
100m
100m
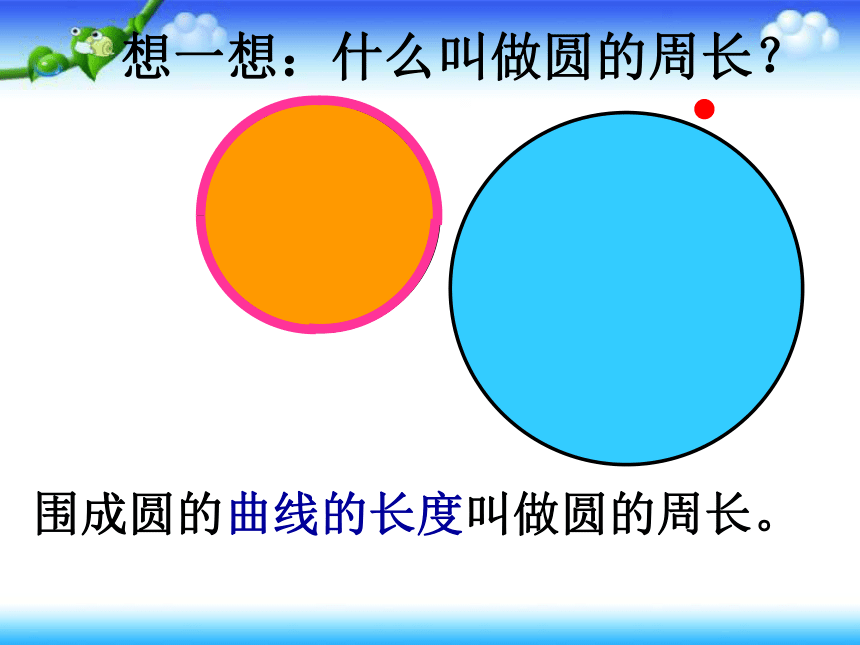
想一想:什么叫做圆的周长?
围成圆的曲线的长度叫做圆的周长。
组内同伴互相说一说
利用手中的工具,怎样测量圆的周长?
绕线法:
绕线法:
绕线法:
绕线法:
绕线法:
0
1
2
3
4
绕线法:
滚动法:
0
1
2
3
4
6
7
8
5
2厘米
太麻烦了,有更简单的办法就好了。
是啊,要是有一个很大的圆怎么测量呢?
要是能像长方形,正方形
那样有公式计算就好啦!
圆的周长跟圆的什么
有关呢?
注意观察,猜猜看:
1.观察这三个圆,看看谁的周长最长?
2.猜猜看,圆的周长与什么有关?
3.圆的周长与直径有怎样的关系?
圆的直径越( ),那么它的周长就越( )
长
长
小组合作,探究新知
每组用自己喜欢的方法去测量大小不同的三个圆,完成表格。
1.小组同学做好分工,组长选好测量员、记 录员、计算员、汇报员。
2.记录员要及时地把测量员测量的数据记录在表格里。
物品名称
周长
(毫米)
直径
(毫米)
(保留两位小数)
一角硬币
手镯
五角硬币
一元硬币
7.5
6.3
22
2
2.4
7
2.2
6.9
3.14
3.15
3.14
3.13
你发现圆的周长和直径之间有什么关系?
一个圆的周长总是它的直径的3倍多一些。
圆的周长是直径的3倍多一些
其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母“π (读pài)”表示。他是一个无限不循环小数,π= 3.1415926535……但在实际应用中一般只取它的近似值,即π≈3.14。
π>3.14
约1500年前,中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在3.1415926 和3.1415927 之间,成为世界上第一个把圆周率的值计算精确到7 位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早一千年。
祖冲之
??圆的周长=直径×圆周率
???????? ???? c=πd??? ??c=2πr
100m
求下面各圆的周长。(只列式不计算)
d=4厘米
r=1.5米
3.14×4
3.14×1.5×2
口答
已知什么?求什么?运用哪个公式?
(1)圆的周长大小由 决定
(2)圆的半径是2cm,则圆的周长是 。
(3)直径为2cm的圆周长是 。
(4)圆周长是15.7cm,则圆的半径是 。
(5)若圆的直径扩大3倍,则圆的周长扩大 倍。
(6)若圆的周长缩小4倍,则圆的直径缩小 倍 ,
半径缩小 倍
直径
12.56cm
6.28cm
2.5cm
3
4
4
填空:
1.判断。
(1)圆周率就是圆的周长和直径的比值。( )
(2)圆的直径越长,圆周率越大。( )
(3)两个圆的周长相等,那么这两个圆的直径也相等.( )
( 4 )圆的直径扩大a倍,那么圆的周长也扩a倍.( )
√
×
√
√
(1)知道圆的直径或半径就可以计算圆的周长。( )
(2)大圆的圆周率大,小圆的圆周率小。 ( )
(3)π等于3.14。 ( )
√
×
×
你能顺利过关吗?
打手势判断
一、选择填空
1、车轮滚动一周,前进的距离是求车轮的( )
A.半径 B.直径 C.周长
2、圆的周长是直径的( )倍。
A. 3.14 B. π C. 3
C
B
3、车轮滚动一周前进1.5米,若滚动3周能前进( )米。
A. 1.5 B. 4.5 C. 6
B
4、大圆的周长除以直径的商( )小
圆的周长除以直径的商。
A. 大于 B. 小于 C.等于
C
C d r c÷d
d π πd 2 r
1
2
我会连
求下面各圆的周长。
d=4厘米
r=1.5米
3.14×4=12.56(厘米)
2×3.14×1.5=9.42(米)
杨老师绕“蓝色星球”的最大横截面走一圈,大约走多少米呢?
3.14×32=100.48(米)
答:大约走100.48米。
d=32米
●
一张圆桌的直径是0.95米。这张圆桌的周长是多少米?
(π取3.14,得数保留两位小数。)
C=
d
π
﹋
3.14×0.95
=2.983
≈2.98(米)
答:这张圆桌的周长大约是2.98米。
例题:
一面圆镜的的镜面直径是40厘米,在它的边缘镶嵌着一根金属条。这根金属条的长至少是多少厘米?
3.14×40=125.6(厘米)
摩天轮的半径是5米,坐着它转动一周,大约转过多少米?(π取3.14)
2×3.14×5=31.4(米)
答:大约在空中转过31.4米。
﹋
C=
r
2π
我的收获
(1)今天我学习了圆周长的知识。我知道圆周率是( )和( )的比值,它用字母( )表示,它是我国古代数学家( )发现的。
直径d
π≈3.14
周长
直径
祖冲之
(2)我还知道圆的周长总是直径的( )倍。已知圆的直径就可以用公式( )求周长;已知圆的半径就可以用公式( )求周长。
π
C=
d
π
C=
r
2π
π
1.求出此图形的周长
4厘米
=3.14×4=12.56(厘米)
此图形的周长为:12.56÷2+4=10.28(厘米)
2.已知长方形的周长是32厘米,长是12厘米,求阴影部分的周长。
解:32÷2-12=4(厘米)
3/4×3.14×4×2+4×2
=26.84(厘米)
答:阴影部分周长为26.84厘米。
C圆=
d
π
100m
不公平
要求圆的周长,需要知道什么条件?
如图,红色跑道为两个直径50m的半圆,蓝色跑道为直径100m的半圆。
大黄狗绕里面的小圈跑(如图红色线条),大黑猫从外圈跑(如图蓝色线条)大黄狗心想从里圈跑要比外面的大圈近,这个第一肯定是拿定了。你们能猜到比赛结果吗?大黄狗的阴谋能得逞吗?
知识拓展
大黄狗和大黑猫又展开了第三场比赛。红色跑道为三个直径分别为50m、30和20m的半圆,蓝色跑道为直径100m的半圆。
大黄狗让大黑猫绕里面的小圈跑(如图红色线条),自己从外圈跑(如图蓝色线条),这次大黄狗能获胜吗?
判断辨析
1、π=3.14 ( )
2、只要知道圆的直径或者半径,就可以知道圆的周长( )
3、大圆的圆周率比小圆的圆周率大。 ( )
×
√
×
选择填空
1、车轮滚动一周,前进的距离是求车轮的( )
A.半径 B.直径 C.周长
2、圆的周长是直径的( )倍。
A. 3.14 B. π C. 3
3、大圆的周长除以直径的商( )小
圆的周长除以直径的商。
A. 大于 B. 小于 C.等于
C
B
C
(1)今天我学习了圆周长的知识。我知道圆周率是( )和( )的比值,它用字母( )表示,它是我国古代数学家( )发现的。
周长
直径
祖冲之
(2)我还知道圆的周长总是直径的( )倍。已知圆的直径就可以用公式( )求周长;已知圆的半径就可以用公式( )求周长。
π
C=
d
π
C=
r
2π
π
汽车轮胎的半径是0.3米,它滚动1圈前进多少米?滚动1000圈前进多少米?
小丽量得一个古代建筑中的大圆柱的周长是4.52米。这个圆柱的直径是多少米?(得数保留一位小数)
小明的妈妈在自家的墙根下建了一个花坛(如图)。你能计算出花坛的周长吗?
8米
学习了这节课你有什么收获?
如果小自行车车轮直径是50厘米,绕花坛一周车轮大约转动多少周?
3.14×0.5=1.57(米)
62.8÷1.57=40(周)
答:大约转动40周。
50 厘米 = 0.5 米
平面上封闭图形一周的长度,就是它的周长。
小组讨论,分享成果
每组成员用自己喜欢的方法去测量大小不同的三个圆,完成表格。
1.组长做好分工,选好测量员、记录员、计算员、汇报员。
2.记录员要做到及时把测量的数据记录在表格里。
发现规律,认识圆周率
项目
周长(厘米)
直径(厘米)
周长与它的直径的比值(保留两位小数)
圆1
1
圆2
2
圆3
3
圆4
4
通过测量和计算,你发现圆的周长和直径之间有什么关系?
一个圆的周长总是直径的3倍多一些。
3.14
3.14
6.28
3.14
9.42
3.14
12.56
3.14
推导公式
圆的周长 ÷ 直径 = 圆周率
C = π d
C = 2 π r
大约1500年前,中国有一位伟大的数学家和天文学家祖冲之,他计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早1000年。
现在人们用计算机算出的圆周率,小数点后面已经达到上亿位。
圆周率的故事
1.小红量得一个古代建筑中的大红圆柱的周 长是4.71 m。这个圆柱的直径是多少米?
2.用一根长62.8cm的铁条焊接成一个圆形铁环,它的半径大约是多少厘米?(接头处忽略不计)
“ 我被主人用一根2米长的绳子拴在了这棵小树上,我把绳子拉直走一圈的路程是多少米呢?”
2米
我走一圈的路程是多少米?
r = 2 m
九年义务教育小学六年级数学上册
学习目标:
1. 知道什么是圆的周长。
2. 理解并掌握圆周率的意义和近似值。
3 .初步理解和掌握圆的周长计算公式,能正确计算圆的周长。
4 .通过了解祖冲之在圆周率方面所作的贡献,渗透爱国主义思想。
学习重点:
???????理解和掌握圆的周长的计算公式。
学习难点:
??? ???对圆周率的认识。
100m
100m
想一想:什么叫做圆的周长?
围成圆的曲线的长度叫做圆的周长。
组内同伴互相说一说
利用手中的工具,怎样测量圆的周长?
绕线法:
绕线法:
绕线法:
绕线法:
绕线法:
0
1
2
3
4
绕线法:
滚动法:
0
1
2
3
4
6
7
8
5
2厘米
太麻烦了,有更简单的办法就好了。
是啊,要是有一个很大的圆怎么测量呢?
要是能像长方形,正方形
那样有公式计算就好啦!
圆的周长跟圆的什么
有关呢?
注意观察,猜猜看:
1.观察这三个圆,看看谁的周长最长?
2.猜猜看,圆的周长与什么有关?
3.圆的周长与直径有怎样的关系?
圆的直径越( ),那么它的周长就越( )
长
长
小组合作,探究新知
每组用自己喜欢的方法去测量大小不同的三个圆,完成表格。
1.小组同学做好分工,组长选好测量员、记 录员、计算员、汇报员。
2.记录员要及时地把测量员测量的数据记录在表格里。
物品名称
周长
(毫米)
直径
(毫米)
(保留两位小数)
一角硬币
手镯
五角硬币
一元硬币
7.5
6.3
22
2
2.4
7
2.2
6.9
3.14
3.15
3.14
3.13
你发现圆的周长和直径之间有什么关系?
一个圆的周长总是它的直径的3倍多一些。
圆的周长是直径的3倍多一些
其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母“π (读pài)”表示。他是一个无限不循环小数,π= 3.1415926535……但在实际应用中一般只取它的近似值,即π≈3.14。
π>3.14
约1500年前,中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在3.1415926 和3.1415927 之间,成为世界上第一个把圆周率的值计算精确到7 位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早一千年。
祖冲之
??圆的周长=直径×圆周率
???????? ???? c=πd??? ??c=2πr
100m
求下面各圆的周长。(只列式不计算)
d=4厘米
r=1.5米
3.14×4
3.14×1.5×2
口答
已知什么?求什么?运用哪个公式?
(1)圆的周长大小由 决定
(2)圆的半径是2cm,则圆的周长是 。
(3)直径为2cm的圆周长是 。
(4)圆周长是15.7cm,则圆的半径是 。
(5)若圆的直径扩大3倍,则圆的周长扩大 倍。
(6)若圆的周长缩小4倍,则圆的直径缩小 倍 ,
半径缩小 倍
直径
12.56cm
6.28cm
2.5cm
3
4
4
填空:
1.判断。
(1)圆周率就是圆的周长和直径的比值。( )
(2)圆的直径越长,圆周率越大。( )
(3)两个圆的周长相等,那么这两个圆的直径也相等.( )
( 4 )圆的直径扩大a倍,那么圆的周长也扩a倍.( )
√
×
√
√
(1)知道圆的直径或半径就可以计算圆的周长。( )
(2)大圆的圆周率大,小圆的圆周率小。 ( )
(3)π等于3.14。 ( )
√
×
×
你能顺利过关吗?
打手势判断
一、选择填空
1、车轮滚动一周,前进的距离是求车轮的( )
A.半径 B.直径 C.周长
2、圆的周长是直径的( )倍。
A. 3.14 B. π C. 3
C
B
3、车轮滚动一周前进1.5米,若滚动3周能前进( )米。
A. 1.5 B. 4.5 C. 6
B
4、大圆的周长除以直径的商( )小
圆的周长除以直径的商。
A. 大于 B. 小于 C.等于
C
C d r c÷d
d π πd 2 r
1
2
我会连
求下面各圆的周长。
d=4厘米
r=1.5米
3.14×4=12.56(厘米)
2×3.14×1.5=9.42(米)
杨老师绕“蓝色星球”的最大横截面走一圈,大约走多少米呢?
3.14×32=100.48(米)
答:大约走100.48米。
d=32米
●
一张圆桌的直径是0.95米。这张圆桌的周长是多少米?
(π取3.14,得数保留两位小数。)
C=
d
π
﹋
3.14×0.95
=2.983
≈2.98(米)
答:这张圆桌的周长大约是2.98米。
例题:
一面圆镜的的镜面直径是40厘米,在它的边缘镶嵌着一根金属条。这根金属条的长至少是多少厘米?
3.14×40=125.6(厘米)
摩天轮的半径是5米,坐着它转动一周,大约转过多少米?(π取3.14)
2×3.14×5=31.4(米)
答:大约在空中转过31.4米。
﹋
C=
r
2π
我的收获
(1)今天我学习了圆周长的知识。我知道圆周率是( )和( )的比值,它用字母( )表示,它是我国古代数学家( )发现的。
直径d
π≈3.14
周长
直径
祖冲之
(2)我还知道圆的周长总是直径的( )倍。已知圆的直径就可以用公式( )求周长;已知圆的半径就可以用公式( )求周长。
π
C=
d
π
C=
r
2π
π
1.求出此图形的周长
4厘米
=3.14×4=12.56(厘米)
此图形的周长为:12.56÷2+4=10.28(厘米)
2.已知长方形的周长是32厘米,长是12厘米,求阴影部分的周长。
解:32÷2-12=4(厘米)
3/4×3.14×4×2+4×2
=26.84(厘米)
答:阴影部分周长为26.84厘米。
C圆=
d
π
100m
不公平
要求圆的周长,需要知道什么条件?
如图,红色跑道为两个直径50m的半圆,蓝色跑道为直径100m的半圆。
大黄狗绕里面的小圈跑(如图红色线条),大黑猫从外圈跑(如图蓝色线条)大黄狗心想从里圈跑要比外面的大圈近,这个第一肯定是拿定了。你们能猜到比赛结果吗?大黄狗的阴谋能得逞吗?
知识拓展
大黄狗和大黑猫又展开了第三场比赛。红色跑道为三个直径分别为50m、30和20m的半圆,蓝色跑道为直径100m的半圆。
大黄狗让大黑猫绕里面的小圈跑(如图红色线条),自己从外圈跑(如图蓝色线条),这次大黄狗能获胜吗?
判断辨析
1、π=3.14 ( )
2、只要知道圆的直径或者半径,就可以知道圆的周长( )
3、大圆的圆周率比小圆的圆周率大。 ( )
×
√
×
选择填空
1、车轮滚动一周,前进的距离是求车轮的( )
A.半径 B.直径 C.周长
2、圆的周长是直径的( )倍。
A. 3.14 B. π C. 3
3、大圆的周长除以直径的商( )小
圆的周长除以直径的商。
A. 大于 B. 小于 C.等于
C
B
C
(1)今天我学习了圆周长的知识。我知道圆周率是( )和( )的比值,它用字母( )表示,它是我国古代数学家( )发现的。
周长
直径
祖冲之
(2)我还知道圆的周长总是直径的( )倍。已知圆的直径就可以用公式( )求周长;已知圆的半径就可以用公式( )求周长。
π
C=
d
π
C=
r
2π
π
汽车轮胎的半径是0.3米,它滚动1圈前进多少米?滚动1000圈前进多少米?
小丽量得一个古代建筑中的大圆柱的周长是4.52米。这个圆柱的直径是多少米?(得数保留一位小数)
小明的妈妈在自家的墙根下建了一个花坛(如图)。你能计算出花坛的周长吗?
8米
学习了这节课你有什么收获?
如果小自行车车轮直径是50厘米,绕花坛一周车轮大约转动多少周?
3.14×0.5=1.57(米)
62.8÷1.57=40(周)
答:大约转动40周。
50 厘米 = 0.5 米
平面上封闭图形一周的长度,就是它的周长。
小组讨论,分享成果
每组成员用自己喜欢的方法去测量大小不同的三个圆,完成表格。
1.组长做好分工,选好测量员、记录员、计算员、汇报员。
2.记录员要做到及时把测量的数据记录在表格里。
发现规律,认识圆周率
项目
周长(厘米)
直径(厘米)
周长与它的直径的比值(保留两位小数)
圆1
1
圆2
2
圆3
3
圆4
4
通过测量和计算,你发现圆的周长和直径之间有什么关系?
一个圆的周长总是直径的3倍多一些。
3.14
3.14
6.28
3.14
9.42
3.14
12.56
3.14
推导公式
圆的周长 ÷ 直径 = 圆周率
C = π d
C = 2 π r
大约1500年前,中国有一位伟大的数学家和天文学家祖冲之,他计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早1000年。
现在人们用计算机算出的圆周率,小数点后面已经达到上亿位。
圆周率的故事
1.小红量得一个古代建筑中的大红圆柱的周 长是4.71 m。这个圆柱的直径是多少米?
2.用一根长62.8cm的铁条焊接成一个圆形铁环,它的半径大约是多少厘米?(接头处忽略不计)
“ 我被主人用一根2米长的绳子拴在了这棵小树上,我把绳子拉直走一圈的路程是多少米呢?”
2米
我走一圈的路程是多少米?
r = 2 m
