人教B版(2019)高中数学选择性必修第一册 1.1.1 空间向量及其运算 课件(50张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 1.1.1 空间向量及其运算 课件(50张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 18:39:01 | ||
图片预览










文档简介
1.1.1 空间向量及其运算
核心素养
1.理解空间向量的概念,掌握空间向量的表示方法.(数学抽象)
2.学会空间向量的线性运算及它们的运算律.(数学运算)
3.能用空间向量的线性运算解决简单的立体几何问题.(逻辑推理)
4.理解空间向量夹角的概念,并掌握两个向量数量积的定义、性质及运算律.(数学抽象)
5.能用两个向量的数量积解决立体几何中的角度和长度等问题.(逻辑推理)
思维脉络
激趣诱思
知识点拨
一天,梭子鱼、虾和天鹅发现路上有一辆车,上面装满了好吃的东西,于是就想把车子从路上拖下来,三个家伙一齐铆足了劲,使出了平生的力气一起拖车,可是,无论它们怎样用力,小车还是在老地方一步也动不了.原来,天鹅使劲往天上提,虾一步步向后倒拖,梭子鱼又朝着池塘拉去.同学们,你们知道这样拉车,车子为什么不动吗?
激趣诱思
知识点拨
1.空间向量的概念
空间向量
空间中既有大小,又有方向的量
零向量、单位向量
始点和终点相同的向量称为零向量,记为0.模等于1的向量称为单位向量,一般记为e
向量的模(或长度)
表示向量a的有向线段的长度,记作|a|
相等向量
大小相等、方向相同的向量
平行向量(或共线向量)
方向相同或者相反的两个非零向量
共面向量
空间中的多个向量,如果表示它们的有向线段通过平移之后,都能在同一平面内
激趣诱思
知识点拨
微判断
(1)两个有共同始点且相等的向量,其终点必相同.( )
(2)两个有公共终点的向量,一定是共线向量.( )
(3)在空间中,任意一个向量都可以进行平移.( )
答案:(1)√ (2)× (3)√
微练习
在平行六面体ABCD-A1B1C1D1中,与向量AD相等的向量共有( )
A.1个 B.2个 C.3个 D.4个
答案:C
激趣诱思
知识点拨
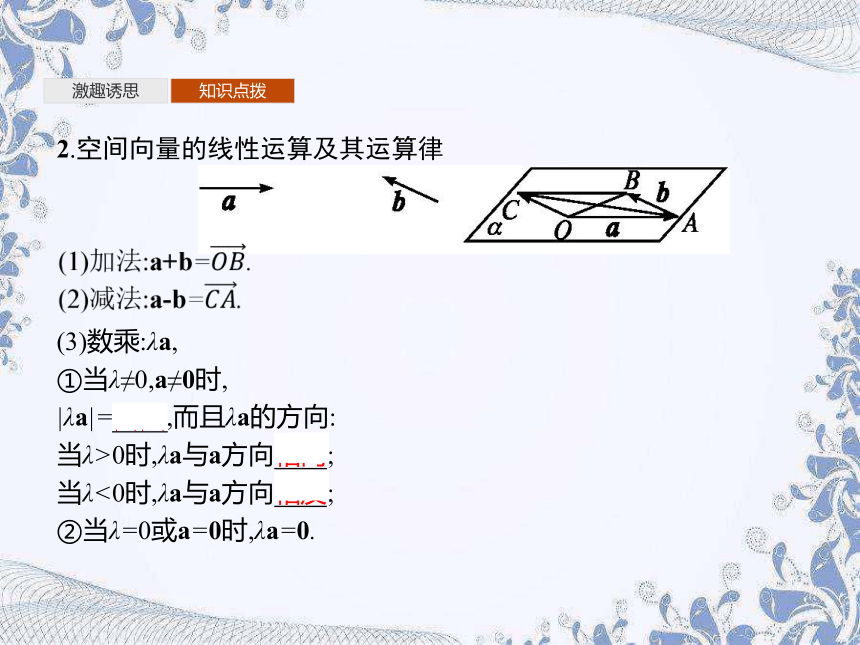
2.空间向量的线性运算及其运算律
(3)数乘:λa,
①当λ≠0,a≠0时,
|λa|=|λ||a|,而且λa的方向:
当λ>0时,λa与a方向相同;
当λ<0时,λa与a方向相反;
②当λ=0或a=0时,λa=0.
激趣诱思
知识点拨
(4)线性运算律
①加法交换律:a+b=b+a;
②加法结合律:(a+b)+c=a+(b+c);
③分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb.
名师点析 空间向量的线性运算中,加法满足三角形法则和平行四边形法则,减法满足三角形法则.
(2)以向量a,b对应的有向线段为邻边的平行四边形中,a+b与a-b对应的有向线段所表示的是两条对角线,|a+b|与|a-b|为两条对角线的长度.
(3)三个不共面的向量和,等于以这三个向量对应的有向线段为邻边的平行六面体中,与这三个向量有共同始点的体对角线所表示的向量.
激趣诱思
知识点拨
微判断
空间中两个非零向量相加时,可以在空间中任取一点作为它们的共同始点.( )
答案:√
微练习1
A.a+b+c B.a+b-c C.a-b-c D.-a+b+c
答案:C
激趣诱思
知识点拨
微练习2
微思考
首尾相接的若干向量若构成一个封闭图形,它们的和向量有什么特点?
提示:和向量为0.
激趣诱思
知识点拨
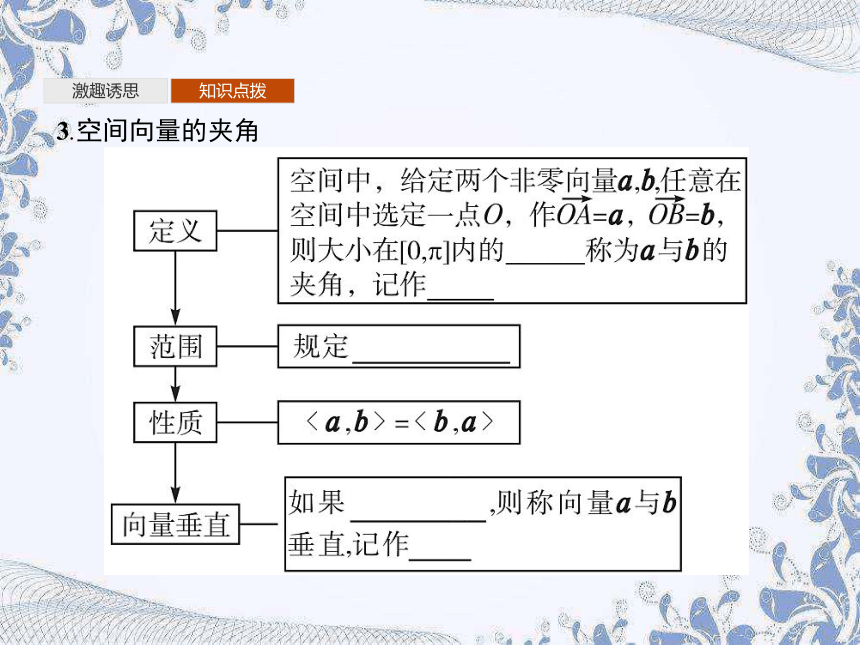
3.空间向量的夹角
激趣诱思
知识点拨
微判断
答案:×
微思考
两个非零向量共线时,其夹角分别是多少?
提示:两个非零向量共线且同向时,=0;两个非零向量共线且反向时,=π.
激趣诱思
知识点拨
4.空间向量的数量积
(1)定义:空间中已知两个非零向量a,b,则|a||b|cos叫做a,b的数量积(也称为内积),记作a·b.即a·b=|a||b|cos.
(2)规定零向量与任意向量的数量积为0.
微判断
若非零向量a,b为共线且同向的向量,则a·b=|a||b|.( )
答案:√
微思考
两个向量的数量积与数乘向量有何不同?
提示:两个向量的数量积是它们的模与其夹角的余弦值的乘积,其结果是实数;数乘向量是一个数与一个向量的乘积,其结果仍是一个向量,如0·a=0,而0·a=0.
激趣诱思
知识点拨
5.空间向量的数量积的性质
(1)a⊥b?a·b=0;
(2)a·a=|a|2=a2;
(3)|a·b|≤|a||b|;
(4)(λa)·b=λ(a·b);
(5)a·b=b·a(交换律);
(6)(a+b)·c=a·c+b·c(分配律).
激趣诱思
知识点拨
名师点析 (1)空间向量的数量积的运算符号是“·”,不能省略,更不能写成“×”;
(2)空间向量的数量积(内积)是一个实数而不是一个向量,它有别于数乘向量;
(3)若a·b=k,不能得出a= ;
(4)a⊥b的充要条件是a·b=0,这是用向量证明空间中垂直关系的根本方法,同时也说明了命题“a·b=0?a=0或b=0”是错误的.
激趣诱思
知识点拨
微判断
(1)对于非零向量b,由a·b=b·c,可得a=c.( )
(2)对于向量a,b,c,有(a·b)·c=a·(b·c).( )
答案:(1)× (2)×
微练习
已知|a|=1,|b|= ,且a-b与a垂直,则a与b的夹角为( )
A.60° B.30° C.135° D.45°
解析:∵a-b与a垂直,∴(a-b)·a=0,
∴a·a-a·b=|a|2-|a|·|b|·cos
答案:D
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
空间向量的概念
例1给出下列命题:①两个空间向量相等,则它们的起点相同,终点也相同;②若空间向量a,b满足|a|=|b|,则a=b;③在正方体ABCD-A1B1C1D1中,必有 ;④若空间向量m,n,p满足m=n,n=p,则m=p;⑤空间中任意两个单位向量必相等.其中正确的个数为( )
A.4 B.3
C.2 D.1
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 解决有关向量概念的问题,要熟练掌握空间向量的有关概念,注意区分向量与向量的模以及数量.相等向量只需方向相同,长度相等,与向量的起点和终点没有必然的联系.尤其要注意解决此类概念问题时,要多结合几何图形进行分析,并要与平面向量中的结论进行类比.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练1下列关于空间向量的说法中正确的是( )
A.空间向量不满足加法结合律
B.若|a|=|b|,则a,b的长度相等而方向相同或相反
D.相等向量其方向必相同
解析:A中,空间向量满足加法结合律;B中,|a|=|b|只能说明a,b的长度相等而方向不确定;C中,向量作为矢量不能比较大小,故选D.
答案:D
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
空间向量的线性运算
例2如图,已知长方体ABCD-A'B'C'D',化简下列向量表达式,并在图中标出化简结果的向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
例3已知在平行六面体ABCD - A'B'C'D'中,M为CC'的中点(如图).化简下列各表达式,并在图中标出化简结果的向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 (1)对于借助几何图形的向量运算,应该在线性运算的基础上挖掘好几何体中本身的特征,如平行、垂直、相等等.
(2)化归与转化思想意识要加强,除借助向量的运算律外,还可以将已知向量转化为与之相等的向量以方便其运算,如例3中第(2)问将
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:A
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
求向量的数量积
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 求两个向量m,n的数量积一般分为两个层次:一是结合图形确定向量m,n的模及的大小,直接利用空间向量数量积的定义来求,此种情况下要注意向量夹角的正确性;二是选定一组基向量表示向量m,n,从而把m,n的数量积通过运算转化为基向量之间的数量积来求.题目中没有明确基底的时候,合理选取基底是至关重要的,比如此题的基底选取既方便向量表示,又方便计算.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练4
如图所示,在棱长为1的正四面体ABCD中,E,F分别是AB,AD的中点,求:
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
利用数量积证明垂直问题
例5
如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
求证:PA⊥BD.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 (1)由数量积的性质a⊥b?a·b=0可知,要证两直线垂直,可构造与两直线分别平行的向量(a,b是非零向量),只要证明这两个向量的数量积为0即可.
(2)用向量法证明线面(面面)垂直,离不开线面(面面)垂直的判定定理,需将线面(面面)垂直转化为线线垂直,然后利用向量法证明线线垂直.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练5如图所示,在正方体ABCD-A1B1C1D1中,O为AC与BD的交点,G为CC1的中点,求证:A1O⊥平面GBD.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
利用数量积求解距离或长度问题
例6平行四边形ABCD中,AB=2AC=2且∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,求B,D间的距离.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 利用向量的数量积求两点间的距离,可以转化为求向量的模的问题,其基本思路是先选择以两点为端点的向量,将此向量表示为几个已知向量的和的形式,求出这几个已知向量的两两之间的夹角以及它们的模,利用公式 求解即可.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练6在平行六面体ABCD-A1B1C1D1中,
AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,求AC1的长.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
易错点——因将向量夹角与直线夹角混淆而致错
案例 如图,空间四边形ABCD中,每条边的长度和两条对角线的长度都等于1,M,N分别是AB,AD的中点,计算
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
1.“两个非零空间向量的模相等”是“两个空间向量相等”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:B
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:D
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
4.若a,b,c为空间两两夹角都是60°的三个单位向量,则|a-b+2c|= .?
解析:|a-b+2c|2=(a-b+2c)2
=a2+b2+4c2-2a·b+4a·c-4b·c
=5.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:60° 1
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
6.已知空间四边形OABC中,M,N,P,Q分别为BC,AC,OA,OB的中点,若AB=OC,求证:PM⊥QN.
核心素养
1.理解空间向量的概念,掌握空间向量的表示方法.(数学抽象)
2.学会空间向量的线性运算及它们的运算律.(数学运算)
3.能用空间向量的线性运算解决简单的立体几何问题.(逻辑推理)
4.理解空间向量夹角的概念,并掌握两个向量数量积的定义、性质及运算律.(数学抽象)
5.能用两个向量的数量积解决立体几何中的角度和长度等问题.(逻辑推理)
思维脉络
激趣诱思
知识点拨
一天,梭子鱼、虾和天鹅发现路上有一辆车,上面装满了好吃的东西,于是就想把车子从路上拖下来,三个家伙一齐铆足了劲,使出了平生的力气一起拖车,可是,无论它们怎样用力,小车还是在老地方一步也动不了.原来,天鹅使劲往天上提,虾一步步向后倒拖,梭子鱼又朝着池塘拉去.同学们,你们知道这样拉车,车子为什么不动吗?
激趣诱思
知识点拨
1.空间向量的概念
空间向量
空间中既有大小,又有方向的量
零向量、单位向量
始点和终点相同的向量称为零向量,记为0.模等于1的向量称为单位向量,一般记为e
向量的模(或长度)
表示向量a的有向线段的长度,记作|a|
相等向量
大小相等、方向相同的向量
平行向量(或共线向量)
方向相同或者相反的两个非零向量
共面向量
空间中的多个向量,如果表示它们的有向线段通过平移之后,都能在同一平面内
激趣诱思
知识点拨
微判断
(1)两个有共同始点且相等的向量,其终点必相同.( )
(2)两个有公共终点的向量,一定是共线向量.( )
(3)在空间中,任意一个向量都可以进行平移.( )
答案:(1)√ (2)× (3)√
微练习
在平行六面体ABCD-A1B1C1D1中,与向量AD相等的向量共有( )
A.1个 B.2个 C.3个 D.4个
答案:C
激趣诱思
知识点拨
2.空间向量的线性运算及其运算律
(3)数乘:λa,
①当λ≠0,a≠0时,
|λa|=|λ||a|,而且λa的方向:
当λ>0时,λa与a方向相同;
当λ<0时,λa与a方向相反;
②当λ=0或a=0时,λa=0.
激趣诱思
知识点拨
(4)线性运算律
①加法交换律:a+b=b+a;
②加法结合律:(a+b)+c=a+(b+c);
③分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb.
名师点析 空间向量的线性运算中,加法满足三角形法则和平行四边形法则,减法满足三角形法则.
(2)以向量a,b对应的有向线段为邻边的平行四边形中,a+b与a-b对应的有向线段所表示的是两条对角线,|a+b|与|a-b|为两条对角线的长度.
(3)三个不共面的向量和,等于以这三个向量对应的有向线段为邻边的平行六面体中,与这三个向量有共同始点的体对角线所表示的向量.
激趣诱思
知识点拨
微判断
空间中两个非零向量相加时,可以在空间中任取一点作为它们的共同始点.( )
答案:√
微练习1
A.a+b+c B.a+b-c C.a-b-c D.-a+b+c
答案:C
激趣诱思
知识点拨
微练习2
微思考
首尾相接的若干向量若构成一个封闭图形,它们的和向量有什么特点?
提示:和向量为0.
激趣诱思
知识点拨
3.空间向量的夹角
激趣诱思
知识点拨
微判断
答案:×
微思考
两个非零向量共线时,其夹角分别是多少?
提示:两个非零向量共线且同向时,
激趣诱思
知识点拨
4.空间向量的数量积
(1)定义:空间中已知两个非零向量a,b,则|a||b|cos
(2)规定零向量与任意向量的数量积为0.
微判断
若非零向量a,b为共线且同向的向量,则a·b=|a||b|.( )
答案:√
微思考
两个向量的数量积与数乘向量有何不同?
提示:两个向量的数量积是它们的模与其夹角的余弦值的乘积,其结果是实数;数乘向量是一个数与一个向量的乘积,其结果仍是一个向量,如0·a=0,而0·a=0.
激趣诱思
知识点拨
5.空间向量的数量积的性质
(1)a⊥b?a·b=0;
(2)a·a=|a|2=a2;
(3)|a·b|≤|a||b|;
(4)(λa)·b=λ(a·b);
(5)a·b=b·a(交换律);
(6)(a+b)·c=a·c+b·c(分配律).
激趣诱思
知识点拨
名师点析 (1)空间向量的数量积的运算符号是“·”,不能省略,更不能写成“×”;
(2)空间向量的数量积(内积)是一个实数而不是一个向量,它有别于数乘向量;
(3)若a·b=k,不能得出a= ;
(4)a⊥b的充要条件是a·b=0,这是用向量证明空间中垂直关系的根本方法,同时也说明了命题“a·b=0?a=0或b=0”是错误的.
激趣诱思
知识点拨
微判断
(1)对于非零向量b,由a·b=b·c,可得a=c.( )
(2)对于向量a,b,c,有(a·b)·c=a·(b·c).( )
答案:(1)× (2)×
微练习
已知|a|=1,|b|= ,且a-b与a垂直,则a与b的夹角为( )
A.60° B.30° C.135° D.45°
解析:∵a-b与a垂直,∴(a-b)·a=0,
∴a·a-a·b=|a|2-|a|·|b|·cos
答案:D
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
空间向量的概念
例1给出下列命题:①两个空间向量相等,则它们的起点相同,终点也相同;②若空间向量a,b满足|a|=|b|,则a=b;③在正方体ABCD-A1B1C1D1中,必有 ;④若空间向量m,n,p满足m=n,n=p,则m=p;⑤空间中任意两个单位向量必相等.其中正确的个数为( )
A.4 B.3
C.2 D.1
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 解决有关向量概念的问题,要熟练掌握空间向量的有关概念,注意区分向量与向量的模以及数量.相等向量只需方向相同,长度相等,与向量的起点和终点没有必然的联系.尤其要注意解决此类概念问题时,要多结合几何图形进行分析,并要与平面向量中的结论进行类比.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练1下列关于空间向量的说法中正确的是( )
A.空间向量不满足加法结合律
B.若|a|=|b|,则a,b的长度相等而方向相同或相反
D.相等向量其方向必相同
解析:A中,空间向量满足加法结合律;B中,|a|=|b|只能说明a,b的长度相等而方向不确定;C中,向量作为矢量不能比较大小,故选D.
答案:D
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
空间向量的线性运算
例2如图,已知长方体ABCD-A'B'C'D',化简下列向量表达式,并在图中标出化简结果的向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
例3已知在平行六面体ABCD - A'B'C'D'中,M为CC'的中点(如图).化简下列各表达式,并在图中标出化简结果的向量.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 (1)对于借助几何图形的向量运算,应该在线性运算的基础上挖掘好几何体中本身的特征,如平行、垂直、相等等.
(2)化归与转化思想意识要加强,除借助向量的运算律外,还可以将已知向量转化为与之相等的向量以方便其运算,如例3中第(2)问将
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:A
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
求向量的数量积
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 求两个向量m,n的数量积一般分为两个层次:一是结合图形确定向量m,n的模及
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练4
如图所示,在棱长为1的正四面体ABCD中,E,F分别是AB,AD的中点,求:
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
利用数量积证明垂直问题
例5
如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
求证:PA⊥BD.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 (1)由数量积的性质a⊥b?a·b=0可知,要证两直线垂直,可构造与两直线分别平行的向量(a,b是非零向量),只要证明这两个向量的数量积为0即可.
(2)用向量法证明线面(面面)垂直,离不开线面(面面)垂直的判定定理,需将线面(面面)垂直转化为线线垂直,然后利用向量法证明线线垂直.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练5如图所示,在正方体ABCD-A1B1C1D1中,O为AC与BD的交点,G为CC1的中点,求证:A1O⊥平面GBD.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
利用数量积求解距离或长度问题
例6平行四边形ABCD中,AB=2AC=2且∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,求B,D间的距离.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
反思感悟 利用向量的数量积求两点间的距离,可以转化为求向量的模的问题,其基本思路是先选择以两点为端点的向量,将此向量表示为几个已知向量的和的形式,求出这几个已知向量的两两之间的夹角以及它们的模,利用公式 求解即可.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
变式训练6在平行六面体ABCD-A1B1C1D1中,
AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,求AC1的长.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
易错点——因将向量夹角与直线夹角混淆而致错
案例 如图,空间四边形ABCD中,每条边的长度和两条对角线的长度都等于1,M,N分别是AB,AD的中点,计算
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
1.“两个非零空间向量的模相等”是“两个空间向量相等”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:B
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:C
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:D
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
4.若a,b,c为空间两两夹角都是60°的三个单位向量,则|a-b+2c|= .?
解析:|a-b+2c|2=(a-b+2c)2
=a2+b2+4c2-2a·b+4a·c-4b·c
=5.
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
答案:60° 1
探究一
探究二
探究三
探究四
探究五
素养形成
当堂检测
6.已知空间四边形OABC中,M,N,P,Q分别为BC,AC,OA,OB的中点,若AB=OC,求证:PM⊥QN.
