人教A版(2019)高中数学选择性必修第一册 1.1.1 空间向量及其线性运算 课件(44张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 1.1.1 空间向量及其线性运算 课件(44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 09:33:25 | ||
图片预览











文档简介
1.1.1 空间向量及其线性运算
激趣诱思
知识点拨
一天,梭子鱼、虾和天鹅发现路上有一辆车装满了好吃的东西,于是就想把车子从路上拖下来,三个家伙一齐铆足了劲,使出了平生的力气一起拖车,可是,无论它们怎样用力,小车还是在老地方一步也不动.原来,天鹅使劲往天上提,虾一步步向后倒拖,梭子鱼又朝着池塘拉去.
同学们,你知道为什么车会一动不动吗?
激趣诱思
知识点拨
一、空间向量的定义及相关概念
1.定义
在空间,我们把具有 和 的量叫做空间向量,空间向量的大小叫做空间向量的 .?
2.空间向量及其模的表示方法
空间向量用字母a,b,c,…表示.若向量a的起点是A,终点是B,则向量a也可以记作 ,其模记
大小
方向
长度或模
激趣诱思
知识点拨
3.空间向量的相关概念
平行或重合
激趣诱思
知识点拨
名师点析1.空间向量只有大小和方向,同向且等长的有向线段表示同一向量或相等向量,即向量可以在空间中平移.
2.我们规定:零向量与任意向量平行,即对于任意向量a,都有0∥a.
激趣诱思
知识点拨
微思考
涉及空间两个向量的问题,平面向量中的有关结论是否仍然适用?
提示:适用.
激趣诱思
知识点拨
微练习
(多选题)下列命题正确的是( )
A.若向量a与b的方向相反,则称向量a与b为相反向量
B.零向量没有方向
C.若a是单位向量,则|a|=1
D.若向量m,n,p满足m=n,n=p,则一定有m=p
答案:CD
解析:单位向量是指模等于1的向量,所以若a是单位向量,则必有|a|=1,即选项C正确;由向量相等的定义,知m与p方向相同,模相等,故一定有m=p,选项D正确.
激趣诱思
知识点拨
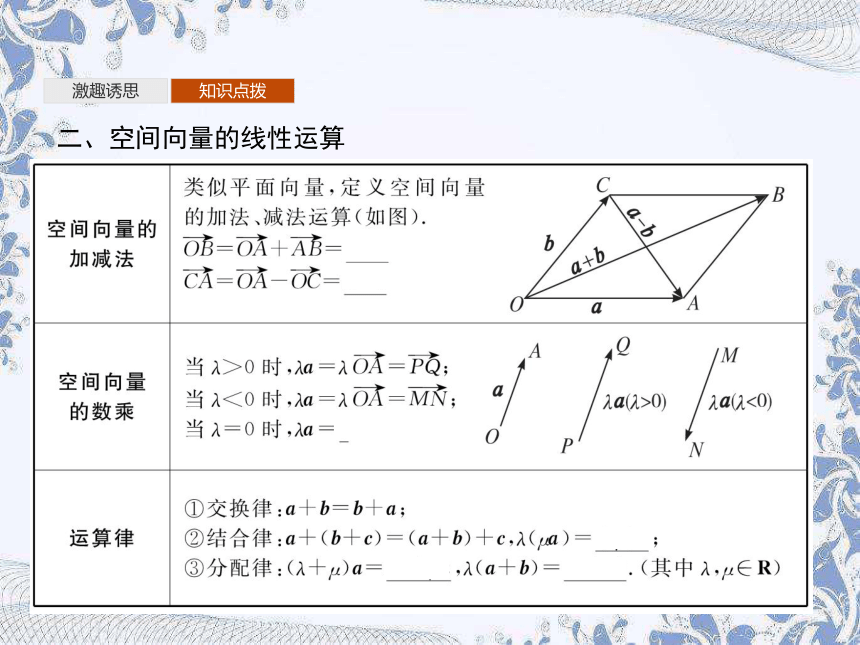
二、空间向量的线性运算
激趣诱思
知识点拨
微练习1
已知空间四边形ABCD中,
A.a+b-c B.c-a-b
C.c+a-b D.c+a+b
答案:B
激趣诱思
知识点拨
微练习2
已知空间四边形ABCD,M,G分别是BC,CD的中点,连接AM,AG,MG,
答案:A
激趣诱思
知识点拨
三、共线向量与共面向量
1.
互相平行或重合
同一个平面
a=λb
p=xa+yb
激趣诱思
知识点拨
激趣诱思
知识点拨
2.如图,O是直线l上一点,在直线l上取非零向量a,则对于直线l上任意一点P,由数乘向量的定义及向量共线的充要条件可知,存在实数λ,使得 =λa.
我们把与向量a平行的非零向量称为直线l的 .这样,直线l上任意一点都可以由直线l上的一点和它的方向向量表示,也就是说,直线可以由其上一点和它的方向向量确定.?
方向向量
激趣诱思
知识点拨
名师点析共线向量的特点及三点共线的充要条件
(1)共线向量不具有传递性
因为零向量0=0·a,所以零向量和空间任一向量a是共线(平行)向量,这一性质使共线向量不具有传递性,即若a∥b,b∥c,则a∥c不一定成立.因为当b=0时,a∥0,0∥c,但a与c不一定共线.
(2)空间三点共线的充要条件
激趣诱思
知识点拨
微练习1
满足下列条件,能说明空间不重合的A,B,C三点共线的是( )
答案:C
激趣诱思
知识点拨
微练习2
对于空间的任意三个向量a,b,2a-b,它们一定是( )
A.共面向量
B.共线向量
C.不共面向量
D.既不共线也不共面的向量
答案:A
解析:因为2a-b=2·a+(-1)·b,
激趣诱思
知识点拨
微判断
判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)若a与b共线,b与c共线,则a与c共线.( )
(2)若向量a,b,c共面,即表示这三个向量的有向线段所在的直线共面.( )
(3)若a∥b,则存在唯一的实数λ,使a=λb.( )
答案: (1)× (2)× (3)×
探究一
探究二
探究三
探究四
素养形成
当堂检测
空间向量及相关概念的理解
解析:①错误,在同一条直线上的单位向量,方向可能相同,也可能相反,故它们不一定相等;
②正确,零向量的模等于0,模等于0的向量只有零向量;
②③
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟空间向量概念的辨析
(1)向量的两个要素是大小与方向,两者缺一不可;
(2)单位向量的方向虽然不一定相同,但长度一定为1;
(3)两个向量的模相等,即它们的长度相等,但方向不确定,即两个向量(非零向量)的模相等是两个向量相等的必要不充分条件;
(4)由于方向不能比较大小,因此“大于”“小于”对向量来说是没有意义的,但向量的模是可以比较大小的.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练1下列说法正确的是( )
A.若|a|=|b|,则a,b的长度相同,方向相同或相反
B.若向量a是向量b的相反向量,则|a|=|b|
C.两个向量相等,若它们的起点相同,则其终点不一定相同
D.若|a|>|b|,|b|>|c|,则a>c
答案:B
解析:两个向量是相反向量时,它们的模必相等,故选项B正确.
探究一
探究二
探究三
探究四
素养形成
当堂检测
空间向量的线性运算
思路分析根据数乘向量及三角形法则,平行四边形法则求解.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟空间向量线性运算的技巧和思路
(1)空间向量加法、减法运算的两个技巧
①巧用相反向量:向量加减法的三角形法则是解决空间向量加法、减法运算的关键,灵活应用相反向量可使有关向量首尾相接,从而便于运算.
②巧用平移:利用三角形法则和平行四边形法则进行向量的加法、减法运算时,务必要注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得更准确的结果.
探究一
探究二
探究三
探究四
素养形成
当堂检测
(2)化简空间向量的常用思路
①分组:合理分组,以便灵活运用三角形法则、平行四边形法则进行化简.
②多边形法则:在空间向量的加法运算中,若是多个向量求和,还可利用多边形法则,若干个向量的和可以将其转化为首尾相接的向量求和.
③走边路:灵活运用空间向量的加法、减法法则,尽量走边路(即沿几何体的边选择途径).
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
空间共线向量定理及其应用
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟利用空间向量共线定理可解决的主要问题
1.判断两向量是否共线:判断两向量a,b(b≠0)是否共线,即判断是否存在实数λ,使a=λb.
2.求解参数:已知两非零向量共线,可求其中参数的值,即利用“若a∥b,则a=λb(λ∈R)”.
3.判断或证明空间中的三点(如P,A,B)是否共线:
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:∵M,N分别是AC,BF的中点,
且四边形ABCD,ABEF都是平行四边形,
探究一
探究二
探究三
探究四
素养形成
当堂检测
空间共面向量定理及其应用
(2)判断点M是否在平面ABC内.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟证明共面问题的基本方法
(1)证明两个空间向量共面时,可以利用共面向量的充要条件,也可直接利用共面向量的定义,通过线面平行、直线在平面内等进行证明.
(2)证明空间四点P,M,A,B共面时,可以通过以下几种条件进行证明.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练4已知A,B,C三点不共线,点O是平面ABC外的任意一点,若点P分别满足下列关系:
试判断点P是否与点A,B,C共面.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
一题多变——空间向量的加法、减法运算
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:(1)根据六棱柱的性质知四边形BB1C1C,DD1E1E都是平行四边形,
探究一
探究二
探究三
探究四
素养形成
当堂检测
方法总结在进行减法运算时,可将减去一个向量转化为加上这个向量的相反向量,而在进行加法运算时,首先考虑这两个向量在哪个平面内,然后与平面向量求和一样,运用向量运算的平行四边形法则、三角形法则及多边形法则来求.
探究一
探究二
探究三
探究四
素养形成
当堂检测
1.“两个非零空间向量的模相等”是“两个空间向量相等”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.在平行六面体ABCD-A‘B’C‘D’中,与向量 相等的向量共有( )
A.1个 B.2个 C.3个 D.4个
答案:B
解析:两个向量相等是指两个向量的模相等并且方向相同,因此“两个非零向量的模相等”是“两个向量相等”的必要不充分条件.
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.如图,在平行六面体ABCD-A1B1C1D1中,点M为A1C1与B1D1的交
答案:B
探究一
探究二
探究三
探究四
素养形成
当堂检测
4.下列条件使点M与点A,B,C一定共面的是( )
答案:D
解析:根据共面向量定理知A,B,C均错,只有D能使其一定共面.
探究一
探究二
探究三
探究四
素养形成
当堂检测
5.如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M,N分别为PC,PD上的点,且PM∶MC=2∶1,N为PD中点,
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:如图,在PD上取一点F,使PF∶FD=2∶1,连接MF,
激趣诱思
知识点拨
一天,梭子鱼、虾和天鹅发现路上有一辆车装满了好吃的东西,于是就想把车子从路上拖下来,三个家伙一齐铆足了劲,使出了平生的力气一起拖车,可是,无论它们怎样用力,小车还是在老地方一步也不动.原来,天鹅使劲往天上提,虾一步步向后倒拖,梭子鱼又朝着池塘拉去.
同学们,你知道为什么车会一动不动吗?
激趣诱思
知识点拨
一、空间向量的定义及相关概念
1.定义
在空间,我们把具有 和 的量叫做空间向量,空间向量的大小叫做空间向量的 .?
2.空间向量及其模的表示方法
空间向量用字母a,b,c,…表示.若向量a的起点是A,终点是B,则向量a也可以记作 ,其模记
大小
方向
长度或模
激趣诱思
知识点拨
3.空间向量的相关概念
平行或重合
激趣诱思
知识点拨
名师点析1.空间向量只有大小和方向,同向且等长的有向线段表示同一向量或相等向量,即向量可以在空间中平移.
2.我们规定:零向量与任意向量平行,即对于任意向量a,都有0∥a.
激趣诱思
知识点拨
微思考
涉及空间两个向量的问题,平面向量中的有关结论是否仍然适用?
提示:适用.
激趣诱思
知识点拨
微练习
(多选题)下列命题正确的是( )
A.若向量a与b的方向相反,则称向量a与b为相反向量
B.零向量没有方向
C.若a是单位向量,则|a|=1
D.若向量m,n,p满足m=n,n=p,则一定有m=p
答案:CD
解析:单位向量是指模等于1的向量,所以若a是单位向量,则必有|a|=1,即选项C正确;由向量相等的定义,知m与p方向相同,模相等,故一定有m=p,选项D正确.
激趣诱思
知识点拨
二、空间向量的线性运算
激趣诱思
知识点拨
微练习1
已知空间四边形ABCD中,
A.a+b-c B.c-a-b
C.c+a-b D.c+a+b
答案:B
激趣诱思
知识点拨
微练习2
已知空间四边形ABCD,M,G分别是BC,CD的中点,连接AM,AG,MG,
答案:A
激趣诱思
知识点拨
三、共线向量与共面向量
1.
互相平行或重合
同一个平面
a=λb
p=xa+yb
激趣诱思
知识点拨
激趣诱思
知识点拨
2.如图,O是直线l上一点,在直线l上取非零向量a,则对于直线l上任意一点P,由数乘向量的定义及向量共线的充要条件可知,存在实数λ,使得 =λa.
我们把与向量a平行的非零向量称为直线l的 .这样,直线l上任意一点都可以由直线l上的一点和它的方向向量表示,也就是说,直线可以由其上一点和它的方向向量确定.?
方向向量
激趣诱思
知识点拨
名师点析共线向量的特点及三点共线的充要条件
(1)共线向量不具有传递性
因为零向量0=0·a,所以零向量和空间任一向量a是共线(平行)向量,这一性质使共线向量不具有传递性,即若a∥b,b∥c,则a∥c不一定成立.因为当b=0时,a∥0,0∥c,但a与c不一定共线.
(2)空间三点共线的充要条件
激趣诱思
知识点拨
微练习1
满足下列条件,能说明空间不重合的A,B,C三点共线的是( )
答案:C
激趣诱思
知识点拨
微练习2
对于空间的任意三个向量a,b,2a-b,它们一定是( )
A.共面向量
B.共线向量
C.不共面向量
D.既不共线也不共面的向量
答案:A
解析:因为2a-b=2·a+(-1)·b,
激趣诱思
知识点拨
微判断
判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)若a与b共线,b与c共线,则a与c共线.( )
(2)若向量a,b,c共面,即表示这三个向量的有向线段所在的直线共面.( )
(3)若a∥b,则存在唯一的实数λ,使a=λb.( )
答案: (1)× (2)× (3)×
探究一
探究二
探究三
探究四
素养形成
当堂检测
空间向量及相关概念的理解
解析:①错误,在同一条直线上的单位向量,方向可能相同,也可能相反,故它们不一定相等;
②正确,零向量的模等于0,模等于0的向量只有零向量;
②③
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟空间向量概念的辨析
(1)向量的两个要素是大小与方向,两者缺一不可;
(2)单位向量的方向虽然不一定相同,但长度一定为1;
(3)两个向量的模相等,即它们的长度相等,但方向不确定,即两个向量(非零向量)的模相等是两个向量相等的必要不充分条件;
(4)由于方向不能比较大小,因此“大于”“小于”对向量来说是没有意义的,但向量的模是可以比较大小的.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练1下列说法正确的是( )
A.若|a|=|b|,则a,b的长度相同,方向相同或相反
B.若向量a是向量b的相反向量,则|a|=|b|
C.两个向量相等,若它们的起点相同,则其终点不一定相同
D.若|a|>|b|,|b|>|c|,则a>c
答案:B
解析:两个向量是相反向量时,它们的模必相等,故选项B正确.
探究一
探究二
探究三
探究四
素养形成
当堂检测
空间向量的线性运算
思路分析根据数乘向量及三角形法则,平行四边形法则求解.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟空间向量线性运算的技巧和思路
(1)空间向量加法、减法运算的两个技巧
①巧用相反向量:向量加减法的三角形法则是解决空间向量加法、减法运算的关键,灵活应用相反向量可使有关向量首尾相接,从而便于运算.
②巧用平移:利用三角形法则和平行四边形法则进行向量的加法、减法运算时,务必要注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得更准确的结果.
探究一
探究二
探究三
探究四
素养形成
当堂检测
(2)化简空间向量的常用思路
①分组:合理分组,以便灵活运用三角形法则、平行四边形法则进行化简.
②多边形法则:在空间向量的加法运算中,若是多个向量求和,还可利用多边形法则,若干个向量的和可以将其转化为首尾相接的向量求和.
③走边路:灵活运用空间向量的加法、减法法则,尽量走边路(即沿几何体的边选择途径).
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
空间共线向量定理及其应用
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟利用空间向量共线定理可解决的主要问题
1.判断两向量是否共线:判断两向量a,b(b≠0)是否共线,即判断是否存在实数λ,使a=λb.
2.求解参数:已知两非零向量共线,可求其中参数的值,即利用“若a∥b,则a=λb(λ∈R)”.
3.判断或证明空间中的三点(如P,A,B)是否共线:
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:∵M,N分别是AC,BF的中点,
且四边形ABCD,ABEF都是平行四边形,
探究一
探究二
探究三
探究四
素养形成
当堂检测
空间共面向量定理及其应用
(2)判断点M是否在平面ABC内.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟证明共面问题的基本方法
(1)证明两个空间向量共面时,可以利用共面向量的充要条件,也可直接利用共面向量的定义,通过线面平行、直线在平面内等进行证明.
(2)证明空间四点P,M,A,B共面时,可以通过以下几种条件进行证明.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练4已知A,B,C三点不共线,点O是平面ABC外的任意一点,若点P分别满足下列关系:
试判断点P是否与点A,B,C共面.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
一题多变——空间向量的加法、减法运算
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:(1)根据六棱柱的性质知四边形BB1C1C,DD1E1E都是平行四边形,
探究一
探究二
探究三
探究四
素养形成
当堂检测
方法总结在进行减法运算时,可将减去一个向量转化为加上这个向量的相反向量,而在进行加法运算时,首先考虑这两个向量在哪个平面内,然后与平面向量求和一样,运用向量运算的平行四边形法则、三角形法则及多边形法则来求.
探究一
探究二
探究三
探究四
素养形成
当堂检测
1.“两个非零空间向量的模相等”是“两个空间向量相等”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.在平行六面体ABCD-A‘B’C‘D’中,与向量 相等的向量共有( )
A.1个 B.2个 C.3个 D.4个
答案:B
解析:两个向量相等是指两个向量的模相等并且方向相同,因此“两个非零向量的模相等”是“两个向量相等”的必要不充分条件.
答案:C
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.如图,在平行六面体ABCD-A1B1C1D1中,点M为A1C1与B1D1的交
答案:B
探究一
探究二
探究三
探究四
素养形成
当堂检测
4.下列条件使点M与点A,B,C一定共面的是( )
答案:D
解析:根据共面向量定理知A,B,C均错,只有D能使其一定共面.
探究一
探究二
探究三
探究四
素养形成
当堂检测
5.如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M,N分别为PC,PD上的点,且PM∶MC=2∶1,N为PD中点,
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:如图,在PD上取一点F,使PF∶FD=2∶1,连接MF,
