2.6 有理数的加减混合运算 课件(共20张PPT)
文档属性
| 名称 | 2.6 有理数的加减混合运算 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
有理数加减混合运算
北师大版
七年级
教学目标
1、初步会用有理数的加减运算法则进行混合运算,并会用运算律进行简化运算。
2、利有有理数的加减混合运算解决一些简单实际问题,使学生初步了解类比学习的思想方法。
3、通过有理数的混合运算解决实际问题,培养学生浓厚的学习兴趣,体会有理数混合运算的意义和作用。
重点、难点
重点:利用有理数的混合运算解决实际问题。
难点:用运算律进行简便计算。
(1)有理数的加法法则是什么?
(2)有理数的减法法则是怎样的?
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不等的异号两数相加,取绝对值较大的加数的符号,并
用较大的绝对值减去较小的绝对值;
(3)互为相反数的两个数相加得零;
(4)一个数与零相加,仍得这个数;
减去一个数,等于加上这个数的相反数.
即
a
-b
=
a
+(-b)
复习回顾
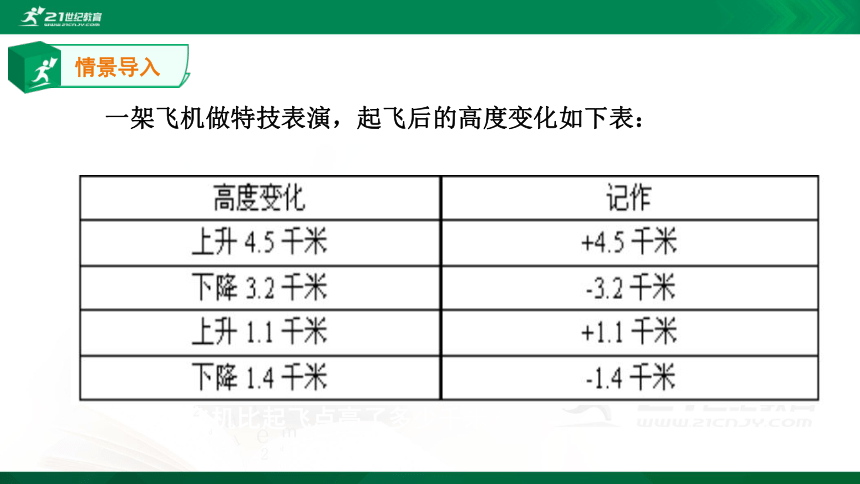
一架飞机做特技表演,起飞后的高度变化如下表:
此时飞机比起飞点高了多少千米?
情景导入
方法一:
4.5+(-3.2)+1.1+(-1.4)
=1.3+1.1+(-1.4)=2.4+(-1.4)
=1(千米)
方法二:
4.5
-
3.2
+
1.1
-
1.4
=
1.3
+
1.1
-
1.4=
2.4
-
1.4
=
1(千米)
那么该飞机最后离起飞点的距离是多少千米?
提出问题
例题讲解
(1)(-)+-
解:原式=(-)-
=(-)+(-)
=
-
(2)(-5)-
(-)+7-
解:原式=
(-5)++7-
=
(-)+7-
=-
=-
=
计算
直接从左往右计算
在代数里,一切加法与减法运算,都可以统一成加法运算。在一个和式里,通常有的加号可以省略,每个数的括号也可以省略。
如4.5+(-3.2)+1.1+(-1.4)可以写成省略括号的形式:
4.5
-
3.2
+
1.1
-
1.4(仍可看作和式)
读作
“正4.5、负3.2、正1.1、负1.4的和”
也可读作
“4.5减3.2加1.1减1.4”
加减法统一成加法
去括号法则
1、括号前是“+”号,去掉括号和它前面的“+”号,括号里面各项都不变;
2、括号前面是“-”号,去掉括号和它前面的“-”号,括号里的各项都变成它的相反数.
(1)
0--
-(-)+(-)
解:原式=0--
+-=(-+)+(--)=(
-+)+(
--)
=
(-)
=-
=-
解题技巧:分母相同或有倍数关系的分数结合相加
(2)(-0.5)-(-)+(+2.75)-(+5.5)
解:原式=(-0.5)+(+0.25)+(+2.75)+(-5.5)=-0.5+0.25+2.75-5.5
=(-0.5-5.5)+(0.25+2.75)=-6+3=-3
解题技巧:在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数
范例讲解
(4)
(-8)
-
(-10)
+
(-6)
-
(+4)
=(-8)
+
(+10)+(-6)
+
(-4)
(把减法运算统一成加法运算
)
=-8+10-6-4
(省略括号和加号)
=-8
读作:
负8
正10
负6
负4
的和.
或:
负8
加10
减6
减4.
这就是省略加号的代数和.
(3)-24+3.2-13+2.8-3
解:原式=(
-24-13-3
)+(
3.2+2.8)=
-40+6=
-34
解题技巧:运用运算律将正负数分别相加。
有理数加减法统一成加法的意义
(1)有理数加减混合运算,可以通过有理数减法法则将减法转化为加法,统一成只有加法运算的和式,如(?12)?(?8)?(?6)?(?5)
?(?12)?(?8)?(?6)?(?5)
(2)在和式里,通常把各个加数的括号和它前面的加号省略不写,写成省略加号的和的形式:如 (?12)?(?8)?(?6)?(?5)
??12?8?6?5
(3)和式的读法,一是按这个式子表示的意义,读作“?12,?8,?6,?5的和”;
二是按运算的意义,读作“负12,减8,减6,加5”。
计算(1)(-)-15
+(-
)
解:原式=(-)+(-15)+(-
=(-)+(-
)+(-15)
=(-
1)+(-15)=-16
解题技巧:有理数加减混合运算,可以通过有理数减法法则将减法转化为加法,统一成只有加法运算的和式.
(2)(-12)-
(-)+(-8)-
解:原式=-12+-8-
=
=-12-8
+-
=-20+=-
解题技巧:在和式里,通常把各个加数的括号和它前面的加号省略不写,写成省略加号的和的形式
例题讲解
(3)
把(+
)-+
-
(-)
-1写成省略加号的和形式,并把它读出来。
(4)如何计算-3+5-9+3+10+2-1比较简便?
-3+5-9+3+10+2-1
=(-3+3)+[(-1-9)+10]+5+2
=0+0+5+2
=7
解题技巧:由于算式可理解为-3,5,-9,3,10,2,-1等七个数的和,因此应用加法结合律、交换律,这七个数可随意结合、交换进行运算,使运算简便。
课堂练习
(1)
-24+3.2-16-3.5+0.3
=(-24-16)+(3.2+0.3)-3.5
=
-40+(3.5-3.5)
=
-40+0
=-40
(2)10-24-15+26-24+18-20
=(10+26+18)+(-24-15-24-20)=54-83=-29
(3)(+0.5)-
+(-
)-(+
)
=(+
)+(
-
)+(-
)
-(+
)
=
-
-
-
=(
-
)+(-
-
)=
-
=-
(4)
某公路养护小组乘车沿南北公路巡护维护。某天早晨从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米):
+18,-9,-7,-14,-6,+13,-6,-8,
问题:B地A地何方?相距多少千米?若汽车行驶每千米耗油a升,求该天共耗油多少升?
分析:将行驶记录相加,若结果为正,则在原出发地A地的正北方向;若结果为负,则在原出发地A地的正南方向。汽车耗油跟方向无关,只跟行驶的总路程有关。而每段路程即记录的绝对值,总路程即每段路程绝对值的和。
解:(+18)+(-9)+(-7)+(-14)+(-6)+(+13)+(-6)+(-8)=-5(千米)
所以,B地在A地的南方,距A地5千米处。
|+18|+|-9|+|-7|+|-14|+|-6|+|+13|+|-6|+|-8|=81(千米)
81X
a=81
a
答:A地在B地的南方距B地5千米。求该天共耗油81
a升
课堂小结
1.加减混合运算的基本步骤
⑴把混合运算中的减法转变为加法,写成前面是加号的形式;
⑵省略加号和括号;
⑶恰当运用加法交换律和结合律简化计算;
⑷在每一步的运算中都须先定符号,后计算数值。
2、加减混合运算的常用方法
⑴按照运算顺序,从左到右逐一加以计算;
⑵把加减法混合运算统一成加法,写成和式的形式后,再运用运算律进行计算。
3、加减混合运算的技巧
(1)运用运算律将正负数分别相加。
(2)分母相同或有倍数关系的分数结合相加。
(3)在式中若既有分数又有小数,把小数统一成分数或把分数统一成小数。
(4)互为相反数的两数可先相加。
(5)带分数整数部分,小数部分可拆开相加。
4、注意点:
⑴在运算熟练之后可以省去减法变加法这一步骤,直接写成省略加号的形式;
⑵在交换数的前后位置时,应连同它前面的符号一起交换;
⑶在进行混合运算时,小学学过的确定运算顺序的方法仍然适用,如果有括号,应先算括号内的。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
有理数加减混合运算
北师大版
七年级
教学目标
1、初步会用有理数的加减运算法则进行混合运算,并会用运算律进行简化运算。
2、利有有理数的加减混合运算解决一些简单实际问题,使学生初步了解类比学习的思想方法。
3、通过有理数的混合运算解决实际问题,培养学生浓厚的学习兴趣,体会有理数混合运算的意义和作用。
重点、难点
重点:利用有理数的混合运算解决实际问题。
难点:用运算律进行简便计算。
(1)有理数的加法法则是什么?
(2)有理数的减法法则是怎样的?
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不等的异号两数相加,取绝对值较大的加数的符号,并
用较大的绝对值减去较小的绝对值;
(3)互为相反数的两个数相加得零;
(4)一个数与零相加,仍得这个数;
减去一个数,等于加上这个数的相反数.
即
a
-b
=
a
+(-b)
复习回顾
一架飞机做特技表演,起飞后的高度变化如下表:
此时飞机比起飞点高了多少千米?
情景导入
方法一:
4.5+(-3.2)+1.1+(-1.4)
=1.3+1.1+(-1.4)=2.4+(-1.4)
=1(千米)
方法二:
4.5
-
3.2
+
1.1
-
1.4
=
1.3
+
1.1
-
1.4=
2.4
-
1.4
=
1(千米)
那么该飞机最后离起飞点的距离是多少千米?
提出问题
例题讲解
(1)(-)+-
解:原式=(-)-
=(-)+(-)
=
-
(2)(-5)-
(-)+7-
解:原式=
(-5)++7-
=
(-)+7-
=-
=-
=
计算
直接从左往右计算
在代数里,一切加法与减法运算,都可以统一成加法运算。在一个和式里,通常有的加号可以省略,每个数的括号也可以省略。
如4.5+(-3.2)+1.1+(-1.4)可以写成省略括号的形式:
4.5
-
3.2
+
1.1
-
1.4(仍可看作和式)
读作
“正4.5、负3.2、正1.1、负1.4的和”
也可读作
“4.5减3.2加1.1减1.4”
加减法统一成加法
去括号法则
1、括号前是“+”号,去掉括号和它前面的“+”号,括号里面各项都不变;
2、括号前面是“-”号,去掉括号和它前面的“-”号,括号里的各项都变成它的相反数.
(1)
0--
-(-)+(-)
解:原式=0--
+-=(-+)+(--)=(
-+)+(
--)
=
(-)
=-
=-
解题技巧:分母相同或有倍数关系的分数结合相加
(2)(-0.5)-(-)+(+2.75)-(+5.5)
解:原式=(-0.5)+(+0.25)+(+2.75)+(-5.5)=-0.5+0.25+2.75-5.5
=(-0.5-5.5)+(0.25+2.75)=-6+3=-3
解题技巧:在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数
范例讲解
(4)
(-8)
-
(-10)
+
(-6)
-
(+4)
=(-8)
+
(+10)+(-6)
+
(-4)
(把减法运算统一成加法运算
)
=-8+10-6-4
(省略括号和加号)
=-8
读作:
负8
正10
负6
负4
的和.
或:
负8
加10
减6
减4.
这就是省略加号的代数和.
(3)-24+3.2-13+2.8-3
解:原式=(
-24-13-3
)+(
3.2+2.8)=
-40+6=
-34
解题技巧:运用运算律将正负数分别相加。
有理数加减法统一成加法的意义
(1)有理数加减混合运算,可以通过有理数减法法则将减法转化为加法,统一成只有加法运算的和式,如(?12)?(?8)?(?6)?(?5)
?(?12)?(?8)?(?6)?(?5)
(2)在和式里,通常把各个加数的括号和它前面的加号省略不写,写成省略加号的和的形式:如 (?12)?(?8)?(?6)?(?5)
??12?8?6?5
(3)和式的读法,一是按这个式子表示的意义,读作“?12,?8,?6,?5的和”;
二是按运算的意义,读作“负12,减8,减6,加5”。
计算(1)(-)-15
+(-
)
解:原式=(-)+(-15)+(-
=(-)+(-
)+(-15)
=(-
1)+(-15)=-16
解题技巧:有理数加减混合运算,可以通过有理数减法法则将减法转化为加法,统一成只有加法运算的和式.
(2)(-12)-
(-)+(-8)-
解:原式=-12+-8-
=
=-12-8
+-
=-20+=-
解题技巧:在和式里,通常把各个加数的括号和它前面的加号省略不写,写成省略加号的和的形式
例题讲解
(3)
把(+
)-+
-
(-)
-1写成省略加号的和形式,并把它读出来。
(4)如何计算-3+5-9+3+10+2-1比较简便?
-3+5-9+3+10+2-1
=(-3+3)+[(-1-9)+10]+5+2
=0+0+5+2
=7
解题技巧:由于算式可理解为-3,5,-9,3,10,2,-1等七个数的和,因此应用加法结合律、交换律,这七个数可随意结合、交换进行运算,使运算简便。
课堂练习
(1)
-24+3.2-16-3.5+0.3
=(-24-16)+(3.2+0.3)-3.5
=
-40+(3.5-3.5)
=
-40+0
=-40
(2)10-24-15+26-24+18-20
=(10+26+18)+(-24-15-24-20)=54-83=-29
(3)(+0.5)-
+(-
)-(+
)
=(+
)+(
-
)+(-
)
-(+
)
=
-
-
-
=(
-
)+(-
-
)=
-
=-
(4)
某公路养护小组乘车沿南北公路巡护维护。某天早晨从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米):
+18,-9,-7,-14,-6,+13,-6,-8,
问题:B地A地何方?相距多少千米?若汽车行驶每千米耗油a升,求该天共耗油多少升?
分析:将行驶记录相加,若结果为正,则在原出发地A地的正北方向;若结果为负,则在原出发地A地的正南方向。汽车耗油跟方向无关,只跟行驶的总路程有关。而每段路程即记录的绝对值,总路程即每段路程绝对值的和。
解:(+18)+(-9)+(-7)+(-14)+(-6)+(+13)+(-6)+(-8)=-5(千米)
所以,B地在A地的南方,距A地5千米处。
|+18|+|-9|+|-7|+|-14|+|-6|+|+13|+|-6|+|-8|=81(千米)
81X
a=81
a
答:A地在B地的南方距B地5千米。求该天共耗油81
a升
课堂小结
1.加减混合运算的基本步骤
⑴把混合运算中的减法转变为加法,写成前面是加号的形式;
⑵省略加号和括号;
⑶恰当运用加法交换律和结合律简化计算;
⑷在每一步的运算中都须先定符号,后计算数值。
2、加减混合运算的常用方法
⑴按照运算顺序,从左到右逐一加以计算;
⑵把加减法混合运算统一成加法,写成和式的形式后,再运用运算律进行计算。
3、加减混合运算的技巧
(1)运用运算律将正负数分别相加。
(2)分母相同或有倍数关系的分数结合相加。
(3)在式中若既有分数又有小数,把小数统一成分数或把分数统一成小数。
(4)互为相反数的两数可先相加。
(5)带分数整数部分,小数部分可拆开相加。
4、注意点:
⑴在运算熟练之后可以省去减法变加法这一步骤,直接写成省略加号的形式;
⑵在交换数的前后位置时,应连同它前面的符号一起交换;
⑶在进行混合运算时,小学学过的确定运算顺序的方法仍然适用,如果有括号,应先算括号内的。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
