人教版八年级数学上册课件:11.3.1多边形(共15张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:11.3.1多边形(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 474.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 09:53:55 | ||
图片预览


文档简介
(共15张PPT)
11.3.1
多边形
什么叫多边形?
由三条或三条以上的线段首尾顺次连接所组成的
平面图形叫做多边形。按照不同的标准,多边形
可以分为正多边形和非正多边形、凸多边形及凹
多边形等
A
B
C
D
E
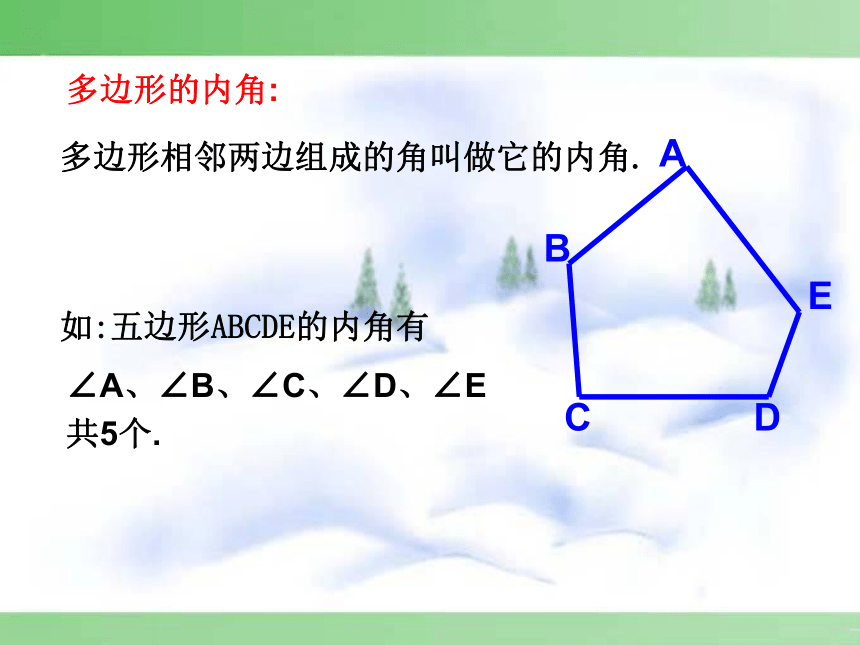
多边形相邻两边组成的角叫做它的内角.
如:五边形ABCDE的内角有
多边形的内角:
∠A、∠B、∠C、∠D、∠E
共5个.
2
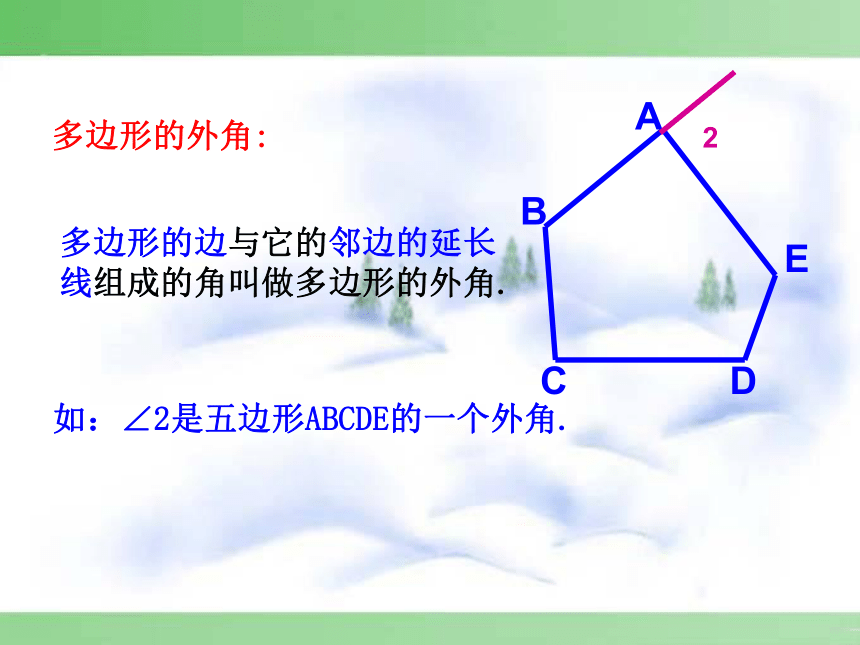
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
如:∠2是五边形ABCDE的一个外角.
多边形的外角:
A
B
C
D
E
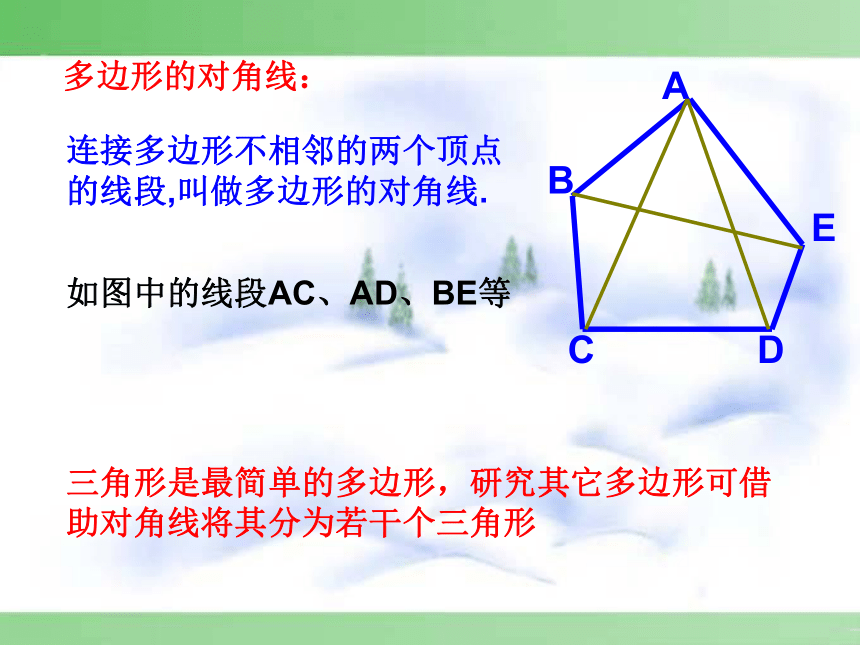
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图中的线段AC、AD、BE等
三角形是最简单的多边形,研究其它多边形可借助对角线将其分为若干个三角形
多边形的对角线:
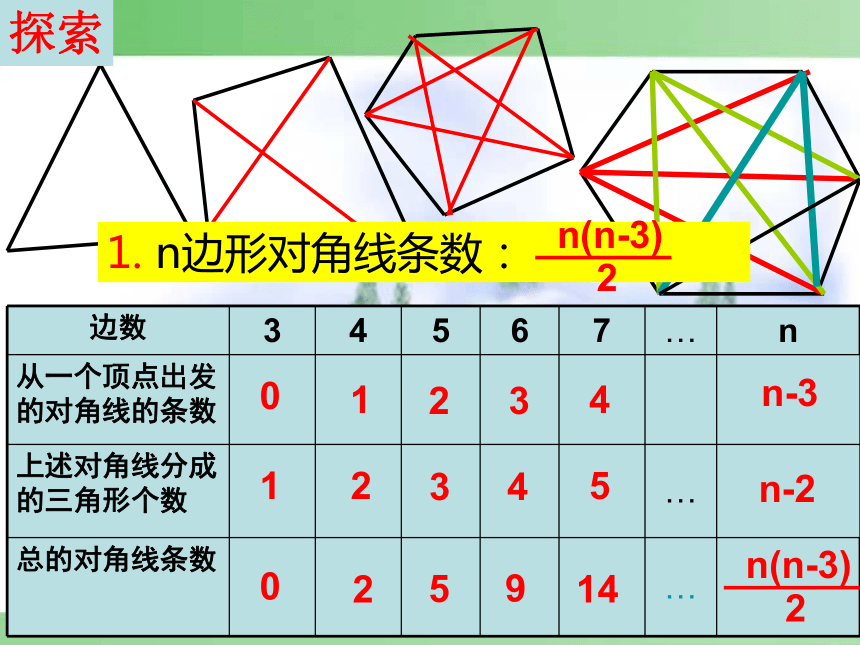
探索
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
边数
3
4
5
6
7
…
n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数
…
总的对角线条数
…
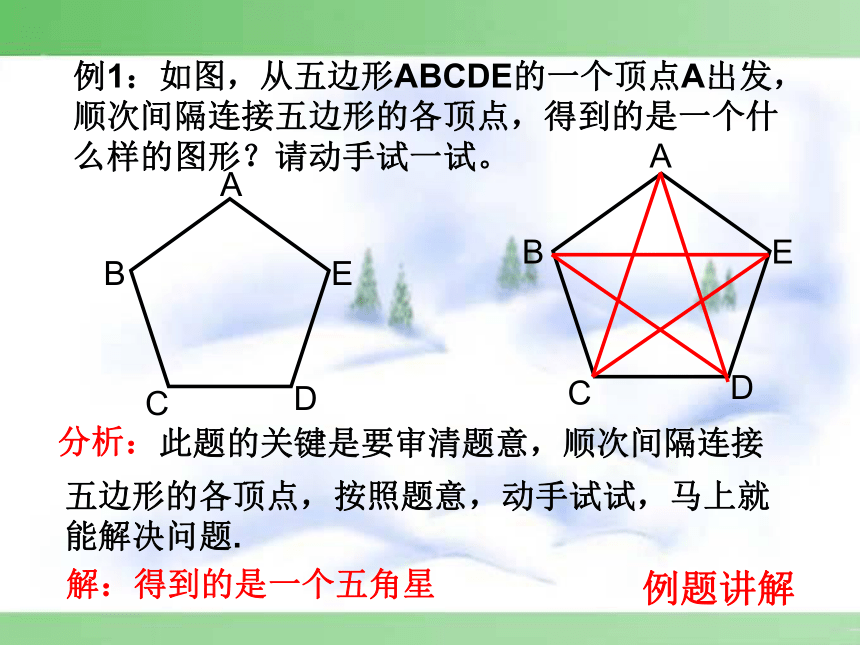
例1:如图,从五边形ABCDE的一个顶点A出发,顺次间隔连接五边形的各顶点,得到的是一个什么样的图形?请动手试一试。
分析:
此题的关键是要审清题意,顺次间隔连接
五边形的各顶点,按照题意,动手试试,马上就能解决问题.
解:得到的是一个五角星
例题讲解
A
B
C
D
图1
图2
图2中,多边形ABCD不在CD所在直线的同侧,就不是凸多边形,叫凹多边形.
在图1中,画出任意一边所在的直线,整个多边形都在直线的同侧,这样的多边形叫做凸多边形.
没有特别说明,我们研究的多边形都是指凸多边形.
多边形的分类
观察图中的多边形,他们的边、角有什么特点?
在平面内,各个角都相等、各条边都相等的多边形叫做正多边形。
正三角形
正方形
正五边形
正六边形
正八边形
正多边形的概念
当n>3时,必须同时满足以下两个条件:
(1)是各边相等,
(2)是各角相等.
两者缺一不可
如长方形各角相等,但各边不一定相等,菱形各边相等,但各角不一定相等,所以它们都不是正多边形。
判断一个n边形是正n边形的条件是:
菱形
矩形
正三角形
正方形
例2:如图,在正方形ABCD中,你能用四种不同的方法把正方形面积四等分吗?
分析:
正方形的面积问题一般可以转化为三角形问题,本题也可以直接把正方形四等分.
解:如图所示
例题讲解
练一练:
1、下列叙述正确的是(
)
A、每条边都相等的多边形是正多边形。
B、如果画出多边形某一条边所在的直线,
这个多边形都在这条直线的同一侧,那么
它一定是凸多边形。
C、每个角都相等的多边形叫正多边形。
D、每条边、每个角都相等的多边形叫正多边形。
2、小学学过的下列图形中不可能是正多边形的是(
)
A、三角形
B、正方形
C、四边形
D、梯形
D
D
3、已知一个多边形有35条对角线,你能求出它的边数吗?
4、如图:∠A=100°,
BD、CD分别平分∠ABC和∠ACB,
求∠BDC的度数。
∠BDC=140°
5、如图:∠A=100°,
∠ABD=30°,∠ACD=35°
求∠BDC的度数。
∠BDC
=165°
11.3.1
多边形
什么叫多边形?
由三条或三条以上的线段首尾顺次连接所组成的
平面图形叫做多边形。按照不同的标准,多边形
可以分为正多边形和非正多边形、凸多边形及凹
多边形等
A
B
C
D
E
多边形相邻两边组成的角叫做它的内角.
如:五边形ABCDE的内角有
多边形的内角:
∠A、∠B、∠C、∠D、∠E
共5个.
2
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
如:∠2是五边形ABCDE的一个外角.
多边形的外角:
A
B
C
D
E
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图中的线段AC、AD、BE等
三角形是最简单的多边形,研究其它多边形可借助对角线将其分为若干个三角形
多边形的对角线:
探索
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
边数
3
4
5
6
7
…
n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数
…
总的对角线条数
…
例1:如图,从五边形ABCDE的一个顶点A出发,顺次间隔连接五边形的各顶点,得到的是一个什么样的图形?请动手试一试。
分析:
此题的关键是要审清题意,顺次间隔连接
五边形的各顶点,按照题意,动手试试,马上就能解决问题.
解:得到的是一个五角星
例题讲解
A
B
C
D
图1
图2
图2中,多边形ABCD不在CD所在直线的同侧,就不是凸多边形,叫凹多边形.
在图1中,画出任意一边所在的直线,整个多边形都在直线的同侧,这样的多边形叫做凸多边形.
没有特别说明,我们研究的多边形都是指凸多边形.
多边形的分类
观察图中的多边形,他们的边、角有什么特点?
在平面内,各个角都相等、各条边都相等的多边形叫做正多边形。
正三角形
正方形
正五边形
正六边形
正八边形
正多边形的概念
当n>3时,必须同时满足以下两个条件:
(1)是各边相等,
(2)是各角相等.
两者缺一不可
如长方形各角相等,但各边不一定相等,菱形各边相等,但各角不一定相等,所以它们都不是正多边形。
判断一个n边形是正n边形的条件是:
菱形
矩形
正三角形
正方形
例2:如图,在正方形ABCD中,你能用四种不同的方法把正方形面积四等分吗?
分析:
正方形的面积问题一般可以转化为三角形问题,本题也可以直接把正方形四等分.
解:如图所示
例题讲解
练一练:
1、下列叙述正确的是(
)
A、每条边都相等的多边形是正多边形。
B、如果画出多边形某一条边所在的直线,
这个多边形都在这条直线的同一侧,那么
它一定是凸多边形。
C、每个角都相等的多边形叫正多边形。
D、每条边、每个角都相等的多边形叫正多边形。
2、小学学过的下列图形中不可能是正多边形的是(
)
A、三角形
B、正方形
C、四边形
D、梯形
D
D
3、已知一个多边形有35条对角线,你能求出它的边数吗?
4、如图:∠A=100°,
BD、CD分别平分∠ABC和∠ACB,
求∠BDC的度数。
∠BDC=140°
5、如图:∠A=100°,
∠ABD=30°,∠ACD=35°
求∠BDC的度数。
∠BDC
=165°
