2.1.2 锐角三角函数(含答案)
图片预览



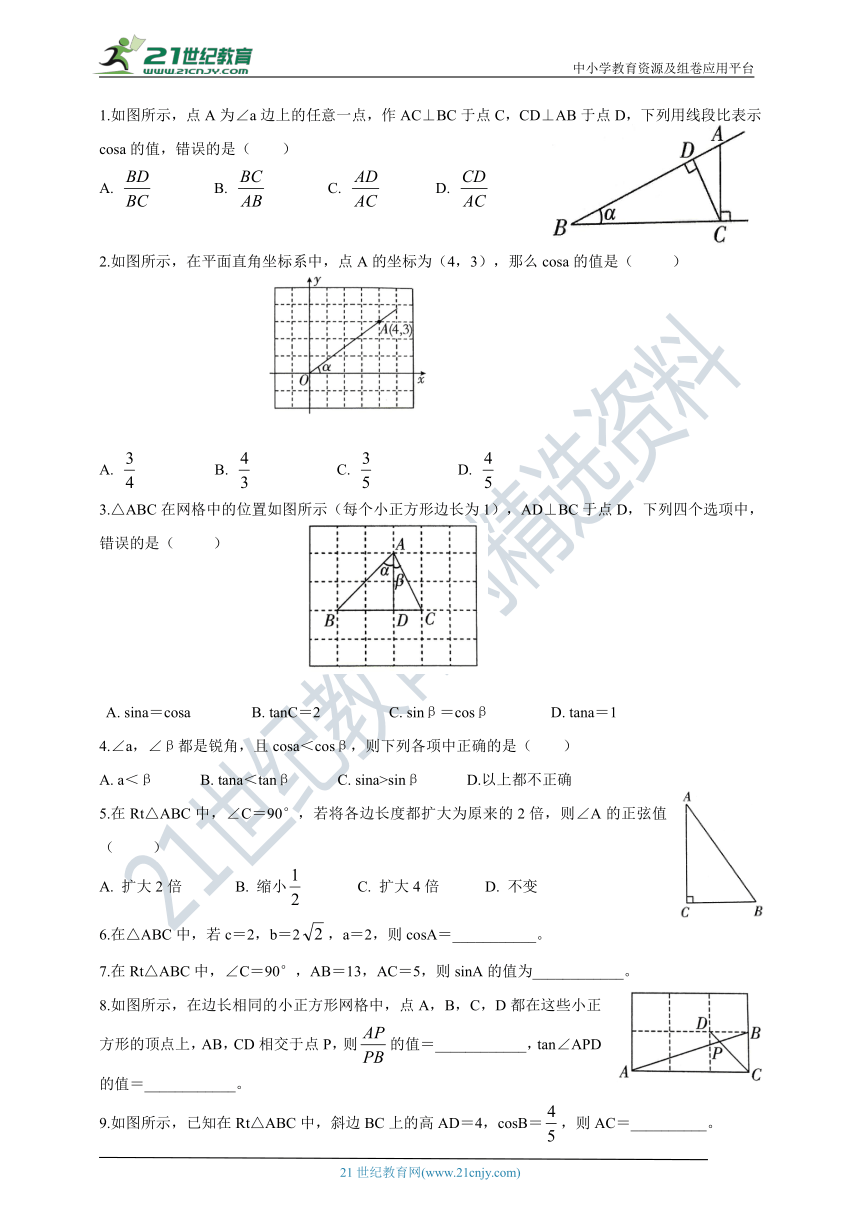
文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
2.1 锐角三角函数
第2课时
知识梳理
知识点1 正弦的定义
定义:如图所示,在Rt△ABC中,∠C=90°,我们把∠A的_________与_________的比叫做∠A的正弦,记作___________,即 sinA=___________。
若AC=4,AB=5,则sinA=____________,sinB=____________。
知识点2 余弦的定义
定义:如上图所示,在Rt△ABC中,∠C=90°,我们把∠A的_________与_________的比叫做∠A的余弦,记作___________,即cosA=____________。
若AC=4,BC=3,则cosA=_________,cosB=__________。
注意(1)正弦、余弦和正切只是数值,没有单位(2)由于斜边大于直角边,所以∠A的正弦、余弦的范围是0<sin<1,0<cosA<1.(3)通常把(sinA)2,(cosA)2,(tanA)2用sin2A,cos2A,tan2A来表示。
知识点3 锐角三角函数的定义
锐角A的___________、___________和__________都是∠A的三角函数,其中∠A的取值范围是0°<∠A<90°.
注意 求锐角三角函数值的实质就是求直角三角形两边的比,而求两边之比的关键是求出直角三角形三边的长或找出三边的关系.
知识点4 梯子倾斜程度与sina,cosA的关系
(1)如图所示,sinA的值越大,梯子AB越_________,AB与AC的夹角越大。
(2)如图所示,cosA的值越小,梯子AB越_________,AB与AC的夹角越大。
考点突破
考点① 求锐角的三角函数值
典例1 如图所示,在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,根据条件求∠A的三个三角函数值.
(1)b=6,c=4;(2)b=a
思路导析:(1)先由勾股定理求出a的值,再根据锐角三角函数的定义求出∠A的三个三角函数值.(2)由b=a,可设a=3x,b=4x,求出c=5x,再根据锐角三角函数的定义求出∠A的三个三角函数值.
解:(1)∵在Rt△ABC中,∠C=90°,b=6,c=4,∴a2=c2-b2=(4)2-62=12.
∴a=2.∴;;。
(2)在Rt△ABC中,∠C=90°,b=a,设a=3x,b=4x,则c=5x.
∴;;。
友情提示 求锐角三角函数值的基本方法是寻求直角三角形三边的关系,再根据定义求解.如果所求三角函数值的角不在直角三角形中,应当转化为直角三角形中的角或构造适当的直角三角形.
变式1 如图所示,在Rt△ABC中,∠C=90°AC=12,BC=5,求∠A,∠B的三个三角函数值.
变式2 如图所示,在等腰三角形ABC中,AB=AC,若BC=AB,求∠B的三个三角函数值。
典例2 在Rt△ABC中,∠C=90°,如果tanA=,那么sinB的值是( )
B. C. D.
思路导析: 如图所示,在Rt△ABC中,∠C=90°,已知tanA=。
设BC=5a,AC=12a 。∵AB2=BC2+AC2,
∴AB=。
∴sinB=。 答案:B
变式3 已知tana=,求sina,cosa的值。
考点2 已知直角三角形一锐角的三角函数值和一边,求其他两边的值
典例3 如图所示,在Rt△ABC中,∠C=90°,sinB=。
(1)若AC=6,求AB,BC的值;
(2)若BC=8,求AB,AC的值。
思路导析:(1)已知AC的值,由sinB==,可直接求出AB=AC=×6=10,再由勾股定理求出BC的值.(2)已知BC的值,由SinB==,可设AC=3k,AB=5k,根据勾股定理得BC=4k。
解:(1)在Rt△ABC中,∠C=90°,∵sinB==,AC=6,∴AB=AC=×6=10.
∴BC===8;
(2)在Rt△ABC中,∠C=90°,∵sinB==,∴设AC=3k,则AB=5k.
∴BC===4k=8.∴k=2.
∴AB=5k=5×2=10,AC=3k=3×2=6.
变式4 在Rt△ABC中,∠C=90°,AB=10.
(1)若sinB=,求AC的长;
(2)若tanA=,求AC的长。
变式5 如图所示,菱形ABCD的周长为40cm,DE⊥AB,垂足为E,sinA=。
(1)求BE的长;
(2)求菱形ABCD的面积。
巩固提高
1.如图所示,点A为∠a边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosa的值,错误的是( )
A. B. C. D.
2.如图所示,在平面直角坐标系中,点A的坐标为(4,3),那么cosa的值是( )
B. C. D.
3.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于点D,下列四个选项中,错误的是( )
A. sina=cosa B. tanC=2 C. sinβ=cosβ D. tana=1
4.∠a,∠β都是锐角,且cosa<cosβ,则下列各项中正确的是( )
A. a<β B. tana<tanβ C. sina>sinβ D.以上都不正确
5.在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的2倍,则∠A的正弦值( )
A. 扩大2倍 B. 缩小 C. 扩大4倍 D. 不变
6.在△ABC中,若c=2,b=2,a=2,则cosA=___________。
7.在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为____________。
8.如图所示,在边长相同的小正方形网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则的值=____________,tan∠APD的值=____________。
9.如图所示,已知在Rt△ABC中,斜边BC上的高AD=4,cosB=,则AC=__________。
10.如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=8,AB=10,求cos∠BCD的值。
11.如图所示,在△ABC中,AB=AC=3,BC=4,求sinB的值.
12.如所示,在△ABC中,∠C=90?,点D在BC上,AD=BC=5,cos∠ADC=,求sinB的值。
13.如图所示,在Rt△ABC中,BC,AC,AB三边的长分别为a,b,c,则sinA=,cosA=,tanA=。我们不难发现:sin2A+cos2A=1…
试探求sinA,cosA,tanA之间存在的一般关系,并说明理由。
体验中考
1.(2018·德州)如图所示,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB=( )
A. B. C. D.
2.(2018·孝感)如图所示,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于( )
A. B. C. D.
3.(2019·雅安)在Rt△ABC中,∠C=90°,AB=5,BC=4,则sinA=____________。
4.(2019·杭州)在直角三角形ABC中,若2AB=AC,则cosC=______________。
参考答案
知识梳理
知识点1: 对边 BC 斜边 AB sinA
知识点2: 邻边AC 斜边AB cosA
知识点3: 正切 正弦 余弦
知识点4:(1)陡 (2)陡
考点突破
1·解:sinA=,cosA=, tanA=。sinB=,cosB=,tanB=.
2,解:sinB=,cosB=,tanB=.
3.解:sina=,cosa=.
4.解:(1)AC=8; (2)AC=8.
5.解:(1) BE=2 cm; (2)菱形ABCD的面积为60 cm2。
巩固提高
1.C 2.D 3.C 4.C 5.D 6. 7. 8. 3 2
9. 5 10. 11.
12.解:∵∠C=90°,AD=BC=5,cos∠ADC=,∴CD=3.
在Rt△ACD中,∵AD=5,CD=3,∴AC===4.
在Rt△ACB中,∵AC=4,BC=5。∴AB===.
∴sinB=。
13.解:存在的一般关系有tanA=
理由:∵sin=,cosA=,∴tanA=。
体验中考
A 2. A 3. 4. 或
_21?????????è?????(www.21cnjy.com)_
第二章 直角三角形的边角关系
2.1 锐角三角函数
第2课时
知识梳理
知识点1 正弦的定义
定义:如图所示,在Rt△ABC中,∠C=90°,我们把∠A的_________与_________的比叫做∠A的正弦,记作___________,即 sinA=___________。
若AC=4,AB=5,则sinA=____________,sinB=____________。
知识点2 余弦的定义
定义:如上图所示,在Rt△ABC中,∠C=90°,我们把∠A的_________与_________的比叫做∠A的余弦,记作___________,即cosA=____________。
若AC=4,BC=3,则cosA=_________,cosB=__________。
注意(1)正弦、余弦和正切只是数值,没有单位(2)由于斜边大于直角边,所以∠A的正弦、余弦的范围是0<sin<1,0<cosA<1.(3)通常把(sinA)2,(cosA)2,(tanA)2用sin2A,cos2A,tan2A来表示。
知识点3 锐角三角函数的定义
锐角A的___________、___________和__________都是∠A的三角函数,其中∠A的取值范围是0°<∠A<90°.
注意 求锐角三角函数值的实质就是求直角三角形两边的比,而求两边之比的关键是求出直角三角形三边的长或找出三边的关系.
知识点4 梯子倾斜程度与sina,cosA的关系
(1)如图所示,sinA的值越大,梯子AB越_________,AB与AC的夹角越大。
(2)如图所示,cosA的值越小,梯子AB越_________,AB与AC的夹角越大。
考点突破
考点① 求锐角的三角函数值
典例1 如图所示,在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,根据条件求∠A的三个三角函数值.
(1)b=6,c=4;(2)b=a
思路导析:(1)先由勾股定理求出a的值,再根据锐角三角函数的定义求出∠A的三个三角函数值.(2)由b=a,可设a=3x,b=4x,求出c=5x,再根据锐角三角函数的定义求出∠A的三个三角函数值.
解:(1)∵在Rt△ABC中,∠C=90°,b=6,c=4,∴a2=c2-b2=(4)2-62=12.
∴a=2.∴;;。
(2)在Rt△ABC中,∠C=90°,b=a,设a=3x,b=4x,则c=5x.
∴;;。
友情提示 求锐角三角函数值的基本方法是寻求直角三角形三边的关系,再根据定义求解.如果所求三角函数值的角不在直角三角形中,应当转化为直角三角形中的角或构造适当的直角三角形.
变式1 如图所示,在Rt△ABC中,∠C=90°AC=12,BC=5,求∠A,∠B的三个三角函数值.
变式2 如图所示,在等腰三角形ABC中,AB=AC,若BC=AB,求∠B的三个三角函数值。
典例2 在Rt△ABC中,∠C=90°,如果tanA=,那么sinB的值是( )
B. C. D.
思路导析: 如图所示,在Rt△ABC中,∠C=90°,已知tanA=。
设BC=5a,AC=12a 。∵AB2=BC2+AC2,
∴AB=。
∴sinB=。 答案:B
变式3 已知tana=,求sina,cosa的值。
考点2 已知直角三角形一锐角的三角函数值和一边,求其他两边的值
典例3 如图所示,在Rt△ABC中,∠C=90°,sinB=。
(1)若AC=6,求AB,BC的值;
(2)若BC=8,求AB,AC的值。
思路导析:(1)已知AC的值,由sinB==,可直接求出AB=AC=×6=10,再由勾股定理求出BC的值.(2)已知BC的值,由SinB==,可设AC=3k,AB=5k,根据勾股定理得BC=4k。
解:(1)在Rt△ABC中,∠C=90°,∵sinB==,AC=6,∴AB=AC=×6=10.
∴BC===8;
(2)在Rt△ABC中,∠C=90°,∵sinB==,∴设AC=3k,则AB=5k.
∴BC===4k=8.∴k=2.
∴AB=5k=5×2=10,AC=3k=3×2=6.
变式4 在Rt△ABC中,∠C=90°,AB=10.
(1)若sinB=,求AC的长;
(2)若tanA=,求AC的长。
变式5 如图所示,菱形ABCD的周长为40cm,DE⊥AB,垂足为E,sinA=。
(1)求BE的长;
(2)求菱形ABCD的面积。
巩固提高
1.如图所示,点A为∠a边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosa的值,错误的是( )
A. B. C. D.
2.如图所示,在平面直角坐标系中,点A的坐标为(4,3),那么cosa的值是( )
B. C. D.
3.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于点D,下列四个选项中,错误的是( )
A. sina=cosa B. tanC=2 C. sinβ=cosβ D. tana=1
4.∠a,∠β都是锐角,且cosa<cosβ,则下列各项中正确的是( )
A. a<β B. tana<tanβ C. sina>sinβ D.以上都不正确
5.在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的2倍,则∠A的正弦值( )
A. 扩大2倍 B. 缩小 C. 扩大4倍 D. 不变
6.在△ABC中,若c=2,b=2,a=2,则cosA=___________。
7.在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为____________。
8.如图所示,在边长相同的小正方形网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则的值=____________,tan∠APD的值=____________。
9.如图所示,已知在Rt△ABC中,斜边BC上的高AD=4,cosB=,则AC=__________。
10.如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=8,AB=10,求cos∠BCD的值。
11.如图所示,在△ABC中,AB=AC=3,BC=4,求sinB的值.
12.如所示,在△ABC中,∠C=90?,点D在BC上,AD=BC=5,cos∠ADC=,求sinB的值。
13.如图所示,在Rt△ABC中,BC,AC,AB三边的长分别为a,b,c,则sinA=,cosA=,tanA=。我们不难发现:sin2A+cos2A=1…
试探求sinA,cosA,tanA之间存在的一般关系,并说明理由。
体验中考
1.(2018·德州)如图所示,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinB=( )
A. B. C. D.
2.(2018·孝感)如图所示,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于( )
A. B. C. D.
3.(2019·雅安)在Rt△ABC中,∠C=90°,AB=5,BC=4,则sinA=____________。
4.(2019·杭州)在直角三角形ABC中,若2AB=AC,则cosC=______________。
参考答案
知识梳理
知识点1: 对边 BC 斜边 AB sinA
知识点2: 邻边AC 斜边AB cosA
知识点3: 正切 正弦 余弦
知识点4:(1)陡 (2)陡
考点突破
1·解:sinA=,cosA=, tanA=。sinB=,cosB=,tanB=.
2,解:sinB=,cosB=,tanB=.
3.解:sina=,cosa=.
4.解:(1)AC=8; (2)AC=8.
5.解:(1) BE=2 cm; (2)菱形ABCD的面积为60 cm2。
巩固提高
1.C 2.D 3.C 4.C 5.D 6. 7. 8. 3 2
9. 5 10. 11.
12.解:∵∠C=90°,AD=BC=5,cos∠ADC=,∴CD=3.
在Rt△ACD中,∵AD=5,CD=3,∴AC===4.
在Rt△ACB中,∵AC=4,BC=5。∴AB===.
∴sinB=。
13.解:存在的一般关系有tanA=
理由:∵sin=,cosA=,∴tanA=。
体验中考
A 2. A 3. 4. 或
_21?????????è?????(www.21cnjy.com)_
