2021中考数学备考经典微专题 《圆的有关计算》专题探究学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 《圆的有关计算》专题探究学案(技巧+满分解答) |

|
|
| 格式 | doc | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《圆的有关计算》专题探究
【考纲要求】
1.会计算圆的弧长和扇形的面积.
2.会计算圆柱和圆锥的侧面积和全面积.
3.了解正多边形的概念及正多边形与圆的关系.
【考点探究】
考点一、弧长、扇形的面积
【例1】如图,在△ABC中,∠B=90°,∠A=30°,AC=4 cm,将△ABC绕顶点C顺时针方向旋转至△A′B′C′的位置,且A,C,B′三点在同一条直线上,则点A所经过的最短路线的长为( )21世纪教育网版权所有
A.4cm B.8 cm C.π cm D.π cm
解析:点A所经过的最短路线是以点C为圆心、CA为半径的一段弧线,运用弧长公式计算求解.求解过程如下:21·cn·jy·com
∵∠B=90°,∠A=30°,A,C,B′三点在同一条直线上,[来源:学科网ZXXK]
∴∠ACA′=120°.又AC=4,
∴的长l==π(cm).故选D.
答案:D[来源:学#科#网Z#X#X#K]
方法总结 当已知半径_r?????????è§????_度数求扇形面积时,应选用S扇=,当已知半径r和弧长求扇形的面积时,应选用公式S扇=lr,当已知半径r和圆心角的度数求弧长时,应选用公式l=.2·1·c·n·j·y
触类旁通1 如图,一扇形纸扇完全打开后,外侧两根竹条A B和AC的夹角为120°,AB长为9,贴纸部分的宽BD为6,则贴纸部分面积(贴纸部分为两面)是( )
A.24π B.36π C.48π D.72π
考点二、圆柱和圆锥
【例2】一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( )
A.5π B.4π C.3π D.2π
解析:侧面积是:×π×22=2π.底面的周长是2π.则底面圆半径是1,面积是π.则该圆锥的全面积是:2π+π=3π.故选C.【来源:21·世纪·教育·网】
答案:C
方法总结 圆锥的侧面展开图是扇形_????????????é???§?_就是圆锥的侧面积,根据半圆的弧长等于圆锥底面圆的周长,即可求得圆锥底面圆的半径,进而求得面积和全面积,正确理解圆锥的底面的周长等于展开图中扇形的弧长是解题的关键.
触类旁通2 如图,把一_????????????12_ cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形纸筒的侧面(衔接处无缝隙且不重叠),则圆锥底面半径是______cm.www-2-1-cnjy-com
考点三、阴影面积的计算
【例3】如图,A_B??????O??????_径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF,EO,若DE=2,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
解:(1)∵直径AB⊥DE,∴CE=DE=.
∵DE平分AO,∴CO=AO=OE.
又∵∠OCE=90°,∴∠CEO=30°.在Rt△COE中,OE===2.∴⊙O的半径为2.
(2)连接OF,如图所示.
在Rt△DCP中,∵∠DPC=45°,
∴∠D=90°-45°=45°.
∴∠EOF=2∠D=90°.
∵S扇形OEF=×π×22=π,S△OEF=×OE×OF=×2×2=2.
∴S阴影=S扇形OEF-S△OEF=π-2.
方法总结 阴影面积的计算方法很多,灵活性强,常采用转化的数学思想:
(1)将所求面积分割后,利用规则图形的面积相互加减求解.
(2)将阴影中某些图形等积变形后移位,重组成规则图形求解.
(3)将所求面积分割后,利用旋转将部分阴影图形移位后,组成规则图形求解.
(4)将阴影图形看成是一些基本图形覆盖而成的重叠部分,用整体和差法求解.
【经典考题】
1.已知一个圆锥的底面半径为3 cm,母线长为10 cm,则这个圆锥的侧面积为( )
A.15π cm2 B.30π cm2 C.60π cm2 D.3cm2
2.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )21cnjy.com
A.cm B.3cm C.4cm D.4 cm
3.一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角是( )
A.120° B.180° C. 240° D.300°
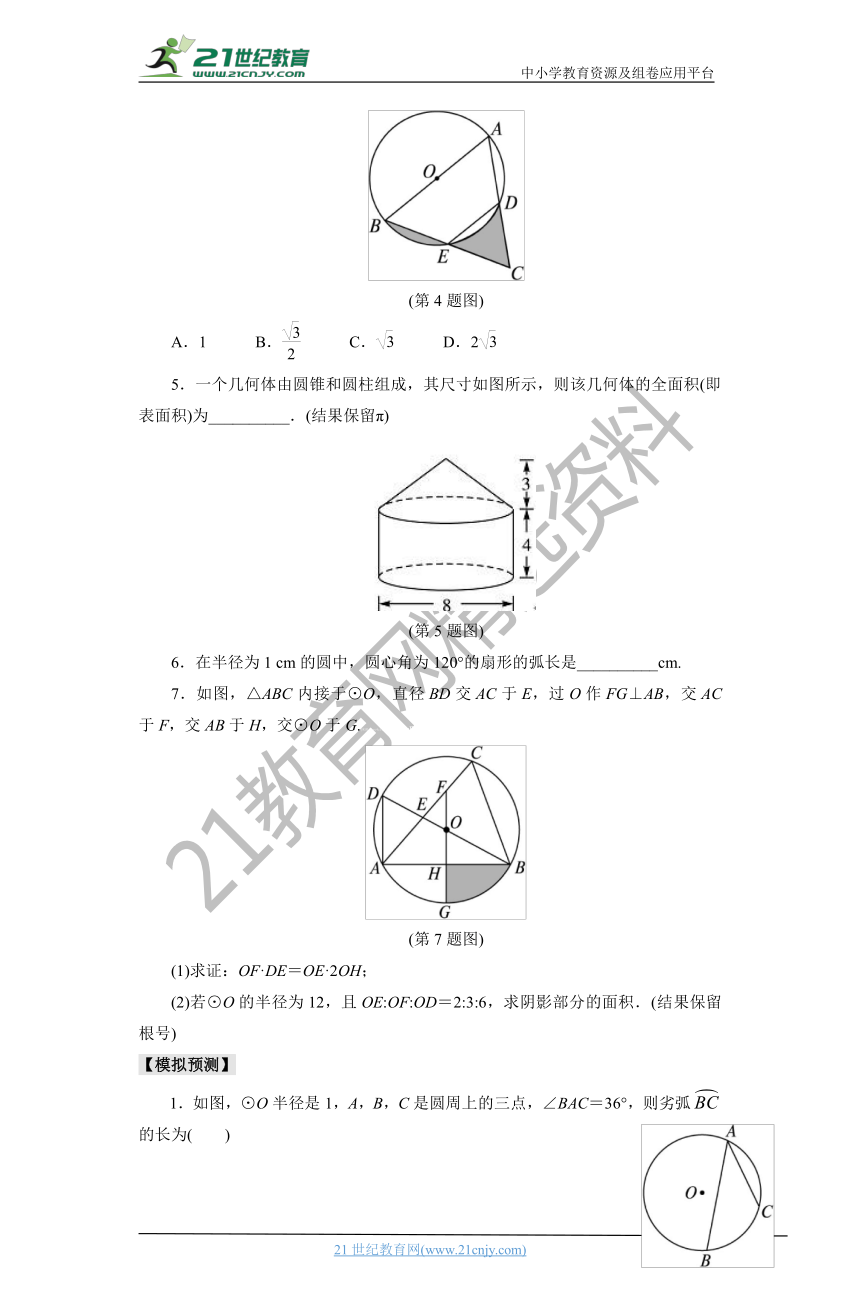
4.如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )www.21-cn-jy.com
(第4题图)
A.1 B. C. D.2
5.一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为__________.(结果保留π)21·世纪*教育网
(第5题图)
6.在半径为1 cm的圆中,圆心角为120°的扇形的弧长是__________cm.
7.如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.[来源:Z+xx+k.Com]2-1-c-n-j-y
(第7题图)
(1)求证:OF·DE=OE·2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)
【模拟预测】
1.如图,⊙O半径是1,A,B,C是圆周上的三点,∠BAC=36°,则劣弧的长为( )
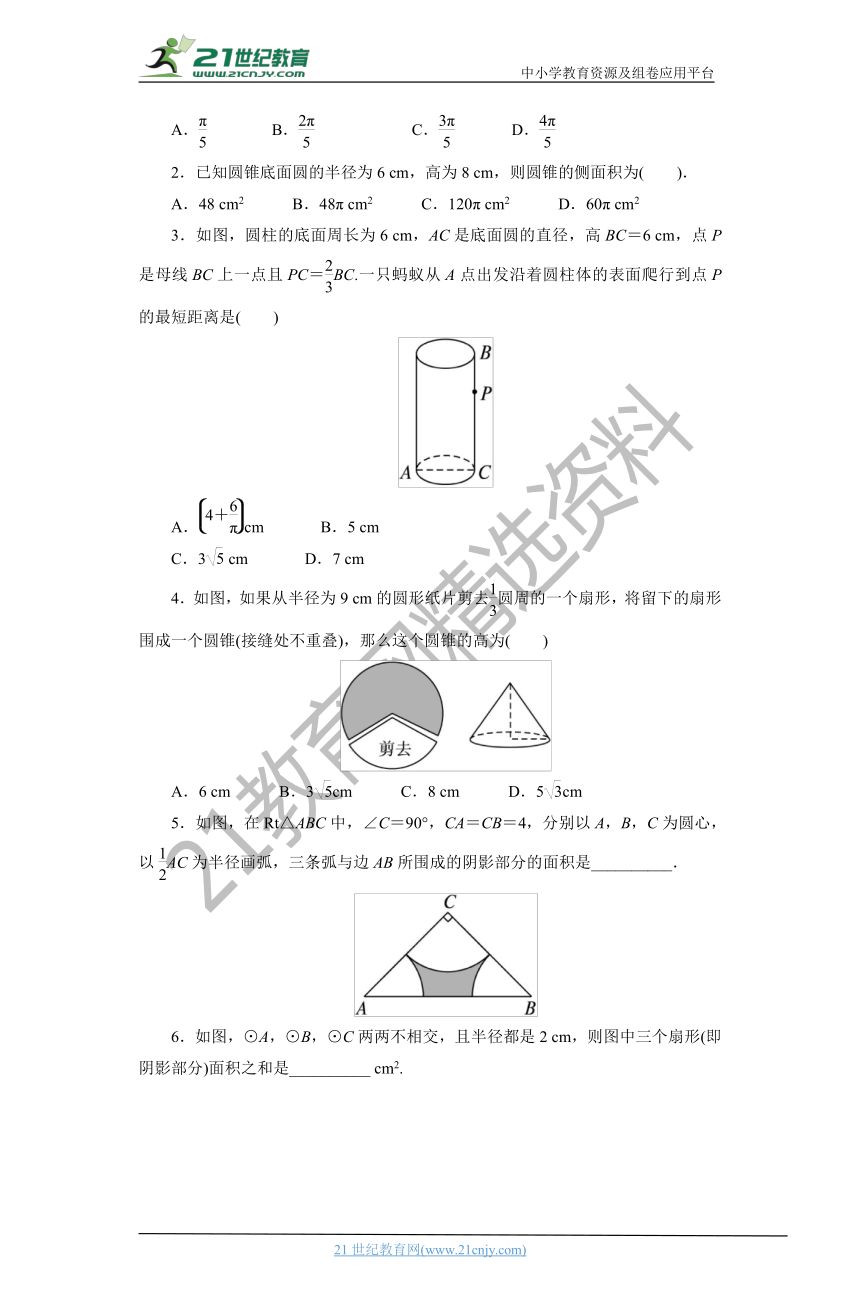
A. B. C. D.
2.已知圆锥底面圆的半径为6 cm,高为8 cm,则圆锥的侧面积为( ).
A.48 cm2 B.48π cm2 C.120π cm2 D.60π cm2
3.如图,圆柱的底面周长为6 cm,AC是底面圆的直径,高BC=6 cm,点P是母线BC上一点且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )21教育网
A.cm B.5 cm
C.3 cm D.7 cm
4.如图,如果从半径为9 cm的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )21*cnjy*com
A.6 cm B.3cm C.8 cm D.5cm
5.如图,在Rt△A_BC?????????C_=90°,CA=CB=4,分别以A,B,C为圆心,以AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是__________.
6.如图,⊙A,⊙B,⊙C两两不相交,且半径都是2 cm,则图中三个扇形(即阴影部分)面积之和是__________ cm2.【来源:21cnj*y.co*m】
(第6题图)
7.如图,AB为半圆O的直径,C,D,E,F是的五等分点,P是AB上的任意一点.若AB=4,则图中阴影部分的面积为__________.
(第7题图)
8.如图,AB是⊙O的直径,弦BC=5,∠BOC=50°,OE⊥AC,垂足为E.
(1)求OE的长;
(2)求劣弧AC的长(结果精确到0.1).
参考答案
【考点探究】
触类旁通1.C S=×2=×2=48π.
触类旁通2.4 因为扇形的弧长为×2×12π=8π,即底面周长为8π,则底面半径为=4(cm).【出处:21教育名师】
【经典考题】
1.B 因为底面半径为3 cm,则周长为6π cm,
所以圆锥的侧面积为6π×10÷2=30π(cm2).
2.C 由题意知l==4π(cm),
圆锥的底面半径为4π÷2π=2(cm),
∴这个圆锥形纸帽的高为=4(cm).[来源:学科网ZXXK]
故选C.
3.B 设圆锥的底面半_??????r?????????_为R,圆锥侧面展开图的扇形的圆心角为n,则扇形的面积为×2πr×R=πrR.由题意得πrR=2πr2,nπR2÷360=πrR,则R=2r,
所以n=180°.
4.C 如图,连接AE.
∵AB是直径,∴∠AEB=90°.
又∵∠BED=120°,∴∠AED=30°,
∴∠AOD=2∠AED=60°.
∵OA=OD,∴△AOD是等边三角形,∴∠OAD=60°.
∵点E为BC的中点,∠AEC=90°,
∴AB=AC,∴△ABC是等边三角形.
由△AOD,△ABC是等边三角形知△DEC,△BOE,△DOE也是等边三角形,
∴和弦BE围成的部分的面积=和弦DE围成的部分的面积,
∴阴影部分的面积=S△EDC=×2×=.故选C.
5.68π 圆锥的母线长是=5,
圆锥的侧面积是×8π×5=20π,
圆柱的侧面积是8π×4=32π,
几何体的下底面面积是π×42=16π,
则该几何体的全面积(即表面积)为20π+32π+16π=68π.
故答案是68π.
6.π 扇形的弧长l==π(cm).
7.(1)证明:∵BD是直径,∴∠DAB=90°.
∵FG⊥AB,∴DA∥FO,
∴∠EOF=∠EDA,∠EFO=∠EAD,
∴△FOE∽△ADE,
∴=,即OF·DE=OE·AD.
∵O是BD的中点,DA∥OH,∴AD=2OH,
∴OF·DE=OE·2OH.
(2)解:∵⊙O的半径为12,且OE:OF:OD=2:3:6,
∴OE=4,ED=8,OF=6,
代入(1)结论得OH=6,AD=12.
在Rt△OBH中,OB=2OH,∴∠BOH=60°,
∴BH=BO·sin 60°=12×=6,
∴S阴影=S扇形GOB-S△OHB=-×6×6=24π-18.
【模拟预测】
1.B 2.D 3.B
4.B 留下的扇形的弧长为×2×π×9=12π,
所以围成一个圆锥的底面圆的周长为12π.[来源:Zxxk.Com]
则底面圆的半径为12π=2πr,所以r=6.
而圆锥的母线长为9,
所以由勾股定理,得到圆锥的高为=3(cm).
5.8-2π 6.2π 7.π
8.解:(1)∵OE⊥AC,垂足为E,∴AE=EC.
∵AO=BO,∴OE=BC=2.5.
(2)∠A=∠BOC=25°,
在Rt△AOE中,sin A=,∴OA=.
∵∠AOC=180°-50°=130°,
∴劣弧AC的长=≈13.4.
_21?????????è?????(www.21cnjy.com)_
《圆的有关计算》专题探究
【考纲要求】
1.会计算圆的弧长和扇形的面积.
2.会计算圆柱和圆锥的侧面积和全面积.
3.了解正多边形的概念及正多边形与圆的关系.
【考点探究】
考点一、弧长、扇形的面积
【例1】如图,在△ABC中,∠B=90°,∠A=30°,AC=4 cm,将△ABC绕顶点C顺时针方向旋转至△A′B′C′的位置,且A,C,B′三点在同一条直线上,则点A所经过的最短路线的长为( )21世纪教育网版权所有
A.4cm B.8 cm C.π cm D.π cm
解析:点A所经过的最短路线是以点C为圆心、CA为半径的一段弧线,运用弧长公式计算求解.求解过程如下:21·cn·jy·com
∵∠B=90°,∠A=30°,A,C,B′三点在同一条直线上,[来源:学科网ZXXK]
∴∠ACA′=120°.又AC=4,
∴的长l==π(cm).故选D.
答案:D[来源:学#科#网Z#X#X#K]
方法总结 当已知半径_r?????????è§????_度数求扇形面积时,应选用S扇=,当已知半径r和弧长求扇形的面积时,应选用公式S扇=lr,当已知半径r和圆心角的度数求弧长时,应选用公式l=.2·1·c·n·j·y
触类旁通1 如图,一扇形纸扇完全打开后,外侧两根竹条A B和AC的夹角为120°,AB长为9,贴纸部分的宽BD为6,则贴纸部分面积(贴纸部分为两面)是( )
A.24π B.36π C.48π D.72π
考点二、圆柱和圆锥
【例2】一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( )
A.5π B.4π C.3π D.2π
解析:侧面积是:×π×22=2π.底面的周长是2π.则底面圆半径是1,面积是π.则该圆锥的全面积是:2π+π=3π.故选C.【来源:21·世纪·教育·网】
答案:C
方法总结 圆锥的侧面展开图是扇形_????????????é???§?_就是圆锥的侧面积,根据半圆的弧长等于圆锥底面圆的周长,即可求得圆锥底面圆的半径,进而求得面积和全面积,正确理解圆锥的底面的周长等于展开图中扇形的弧长是解题的关键.
触类旁通2 如图,把一_????????????12_ cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形纸筒的侧面(衔接处无缝隙且不重叠),则圆锥底面半径是______cm.www-2-1-cnjy-com
考点三、阴影面积的计算
【例3】如图,A_B??????O??????_径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF,EO,若DE=2,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
解:(1)∵直径AB⊥DE,∴CE=DE=.
∵DE平分AO,∴CO=AO=OE.
又∵∠OCE=90°,∴∠CEO=30°.在Rt△COE中,OE===2.∴⊙O的半径为2.
(2)连接OF,如图所示.
在Rt△DCP中,∵∠DPC=45°,
∴∠D=90°-45°=45°.
∴∠EOF=2∠D=90°.
∵S扇形OEF=×π×22=π,S△OEF=×OE×OF=×2×2=2.
∴S阴影=S扇形OEF-S△OEF=π-2.
方法总结 阴影面积的计算方法很多,灵活性强,常采用转化的数学思想:
(1)将所求面积分割后,利用规则图形的面积相互加减求解.
(2)将阴影中某些图形等积变形后移位,重组成规则图形求解.
(3)将所求面积分割后,利用旋转将部分阴影图形移位后,组成规则图形求解.
(4)将阴影图形看成是一些基本图形覆盖而成的重叠部分,用整体和差法求解.
【经典考题】
1.已知一个圆锥的底面半径为3 cm,母线长为10 cm,则这个圆锥的侧面积为( )
A.15π cm2 B.30π cm2 C.60π cm2 D.3cm2
2.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )21cnjy.com
A.cm B.3cm C.4cm D.4 cm
3.一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角是( )
A.120° B.180° C. 240° D.300°
4.如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )www.21-cn-jy.com
(第4题图)
A.1 B. C. D.2
5.一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为__________.(结果保留π)21·世纪*教育网
(第5题图)
6.在半径为1 cm的圆中,圆心角为120°的扇形的弧长是__________cm.
7.如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.[来源:Z+xx+k.Com]2-1-c-n-j-y
(第7题图)
(1)求证:OF·DE=OE·2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)
【模拟预测】
1.如图,⊙O半径是1,A,B,C是圆周上的三点,∠BAC=36°,则劣弧的长为( )
A. B. C. D.
2.已知圆锥底面圆的半径为6 cm,高为8 cm,则圆锥的侧面积为( ).
A.48 cm2 B.48π cm2 C.120π cm2 D.60π cm2
3.如图,圆柱的底面周长为6 cm,AC是底面圆的直径,高BC=6 cm,点P是母线BC上一点且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )21教育网
A.cm B.5 cm
C.3 cm D.7 cm
4.如图,如果从半径为9 cm的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )21*cnjy*com
A.6 cm B.3cm C.8 cm D.5cm
5.如图,在Rt△A_BC?????????C_=90°,CA=CB=4,分别以A,B,C为圆心,以AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是__________.
6.如图,⊙A,⊙B,⊙C两两不相交,且半径都是2 cm,则图中三个扇形(即阴影部分)面积之和是__________ cm2.【来源:21cnj*y.co*m】
(第6题图)
7.如图,AB为半圆O的直径,C,D,E,F是的五等分点,P是AB上的任意一点.若AB=4,则图中阴影部分的面积为__________.
(第7题图)
8.如图,AB是⊙O的直径,弦BC=5,∠BOC=50°,OE⊥AC,垂足为E.
(1)求OE的长;
(2)求劣弧AC的长(结果精确到0.1).
参考答案
【考点探究】
触类旁通1.C S=×2=×2=48π.
触类旁通2.4 因为扇形的弧长为×2×12π=8π,即底面周长为8π,则底面半径为=4(cm).【出处:21教育名师】
【经典考题】
1.B 因为底面半径为3 cm,则周长为6π cm,
所以圆锥的侧面积为6π×10÷2=30π(cm2).
2.C 由题意知l==4π(cm),
圆锥的底面半径为4π÷2π=2(cm),
∴这个圆锥形纸帽的高为=4(cm).[来源:学科网ZXXK]
故选C.
3.B 设圆锥的底面半_??????r?????????_为R,圆锥侧面展开图的扇形的圆心角为n,则扇形的面积为×2πr×R=πrR.由题意得πrR=2πr2,nπR2÷360=πrR,则R=2r,
所以n=180°.
4.C 如图,连接AE.
∵AB是直径,∴∠AEB=90°.
又∵∠BED=120°,∴∠AED=30°,
∴∠AOD=2∠AED=60°.
∵OA=OD,∴△AOD是等边三角形,∴∠OAD=60°.
∵点E为BC的中点,∠AEC=90°,
∴AB=AC,∴△ABC是等边三角形.
由△AOD,△ABC是等边三角形知△DEC,△BOE,△DOE也是等边三角形,
∴和弦BE围成的部分的面积=和弦DE围成的部分的面积,
∴阴影部分的面积=S△EDC=×2×=.故选C.
5.68π 圆锥的母线长是=5,
圆锥的侧面积是×8π×5=20π,
圆柱的侧面积是8π×4=32π,
几何体的下底面面积是π×42=16π,
则该几何体的全面积(即表面积)为20π+32π+16π=68π.
故答案是68π.
6.π 扇形的弧长l==π(cm).
7.(1)证明:∵BD是直径,∴∠DAB=90°.
∵FG⊥AB,∴DA∥FO,
∴∠EOF=∠EDA,∠EFO=∠EAD,
∴△FOE∽△ADE,
∴=,即OF·DE=OE·AD.
∵O是BD的中点,DA∥OH,∴AD=2OH,
∴OF·DE=OE·2OH.
(2)解:∵⊙O的半径为12,且OE:OF:OD=2:3:6,
∴OE=4,ED=8,OF=6,
代入(1)结论得OH=6,AD=12.
在Rt△OBH中,OB=2OH,∴∠BOH=60°,
∴BH=BO·sin 60°=12×=6,
∴S阴影=S扇形GOB-S△OHB=-×6×6=24π-18.
【模拟预测】
1.B 2.D 3.B
4.B 留下的扇形的弧长为×2×π×9=12π,
所以围成一个圆锥的底面圆的周长为12π.[来源:Zxxk.Com]
则底面圆的半径为12π=2πr,所以r=6.
而圆锥的母线长为9,
所以由勾股定理,得到圆锥的高为=3(cm).
5.8-2π 6.2π 7.π
8.解:(1)∵OE⊥AC,垂足为E,∴AE=EC.
∵AO=BO,∴OE=BC=2.5.
(2)∠A=∠BOC=25°,
在Rt△AOE中,sin A=,∴OA=.
∵∠AOC=180°-50°=130°,
∴劣弧AC的长=≈13.4.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
