2021中考数学备考经典微专题 《三角形与全等三角形》考点探究学案(技巧+满分解答)
文档属性
| 名称 | 2021中考数学备考经典微专题 《三角形与全等三角形》考点探究学案(技巧+满分解答) |

|
|
| 格式 | doc | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《三角形与全等三角形》考点探究
【考纲要求】
1.了解三角形和全等三角形有关的概念,知道三角形的稳定性,掌握三角形的三边关系.[来源:Zxxk.Com]21世纪教育网版权所有
2.理解三角形内角和定理及推论.
3.理解三角形的角平分线、中线、高的概念及画法和性质.
4.掌握三角形全等的性质与判定,熟练掌握三角形全等的证明.
【考点探究】
考点一、三角形的边角关系
【例1】若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是( )
A.1 B.5 C.7 D.9
解析:设第三边为x,根据三角形三边的关系可得4-3<x<3+4,即1<x<7.
答案:B
方法总结 1.在具体判断时,可用_è???°??????¤??????_段的和与最长的线段进行比较.若这两条线段的和大于最长的那条线段,则这三条线段能组成三角形.否则就不能组成三角形.21cnjy.com
2.三角形边的关系的应用:(1)判定三条线段是否构成三角形;(2)已知两边的长,确定第三边的取值范围;(3)可证明线段之间的不等关系.
触类旁通1 已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A.2 B.3 C.5 D.13
考点二、全等三角形的性质与判定
【例2】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板AED如图放置,使三角板斜边的两个端点分别与A,D重合,连接BE,EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
解:BE=EC,BE⊥EC.证明如下:
∵AC=2AB,点D是AC的中点,∴AB=AD=CD.
∵∠EAD=∠EDA=45°,∴∠EAB=∠EDC=135°.
又∵EA=ED,∴△EAB≌△EDC.∴∠AEB=∠DEC,EB=EC.∴∠BEC=∠AED=90°.∴BE=EC,BE⊥EC.21·cn·jy·com
方法总结 1.判定两个三角形全等时,常用下面的思路:有两角对应相等时找夹边或任一边对应相等;有两边对应相等时找夹角或另一边对应相等.在具体的证明中,要根据已知条件灵活选择证明方法.www.21-cn-jy.com
2.全等三角形的性质主要是指全等三角形的对应边、对应角、对应中线、对应高、对应角平分线、周长、面积等之间的等量关系.21·世纪*教育网
触类旁通2 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.www-2-1-cnjy-com
求证:△BEC≌△CDA.
考点三、真假命题的判断
【例3】下列命题,正确的是( )
A.如果|a|=|b|,那么a=b
B.等腰梯形的对角线互相垂直
C.顺次连接四边形各边中点所得到的四边形是平行四边形
D.相等的圆周角所对的弧相等[来源:学科网ZXXK]
解析:A项错误,例_??????|???2|_=|2|,但-2≠2;B项错误,等腰梯形的对角线可能垂直,但并不是所有的等腰梯形对角线都垂直;C项正确,可以根据三角形中位线定理和平行四边形的判定得到;D项错误,相等的圆周角所对的弧相等,必须是在同圆或等圆中.21*cnjy*com
答案:C
方法总结 对命题的正确性理解一定要准确,判定命题不成立时,有时可以举反例说明道理;命题有正、误,错误的命题也是命题.2-1-c-n-j-y
触类旁通3 已_??????????????????_直线a,b,c在同一平面内,下列四个命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.其中为真命题的是__________.(填写所有真命题的序号)21*cnjy*com
考点四、证明的方法
【例4】如图,已知在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.
求证:(1)△BFC≌△DFC;
(2)AD=DE.
证明:(1)∵CF平分∠BCD,∴∠BCF=∠DCF.
在△BFC和△DFC中,
∴△BFC≌△DFC.
(2)如图,连接BD.
∵△BFC≌△DFC,
∴BF=DF.∴∠FBD=∠FDB.
∵DF∥AB,∴∠ABD=∠FDB.
∴∠ABD=∠FBD.
∵AD∥BC,∴∠BDA=∠DBC.
∵BC=DC,∴∠DBC=∠BDC.
∴∠BDA=∠BDC.
又BD是公共边,∴△BAD≌△BED.∴AD=DE.
方法总结 1.证明问题时,首先要理清证明的思路,做到证明过程的每一步都有理有据,推理严密.要证明线段、角相等时,证全等是常用的方法.
2.证明的基本方法:(1)综合法,从已知条件入手,探索解题途径的方法;
(2)分析法,从结论出发,用倒推来寻求证题思路的方法;
(3)两头“凑”的方法,综合应用以上两种方法找证明思路的方法.
触类旁通4 如图,在△ABC中,AD是中线,分别过点B,C作AD及其延长线的垂线BE,CF,垂足分别为点E,F.求证:BE=CF.21教育网
【经典考题】
1.(浙江嘉兴)已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
A.40° B.60° C.80° D.90°
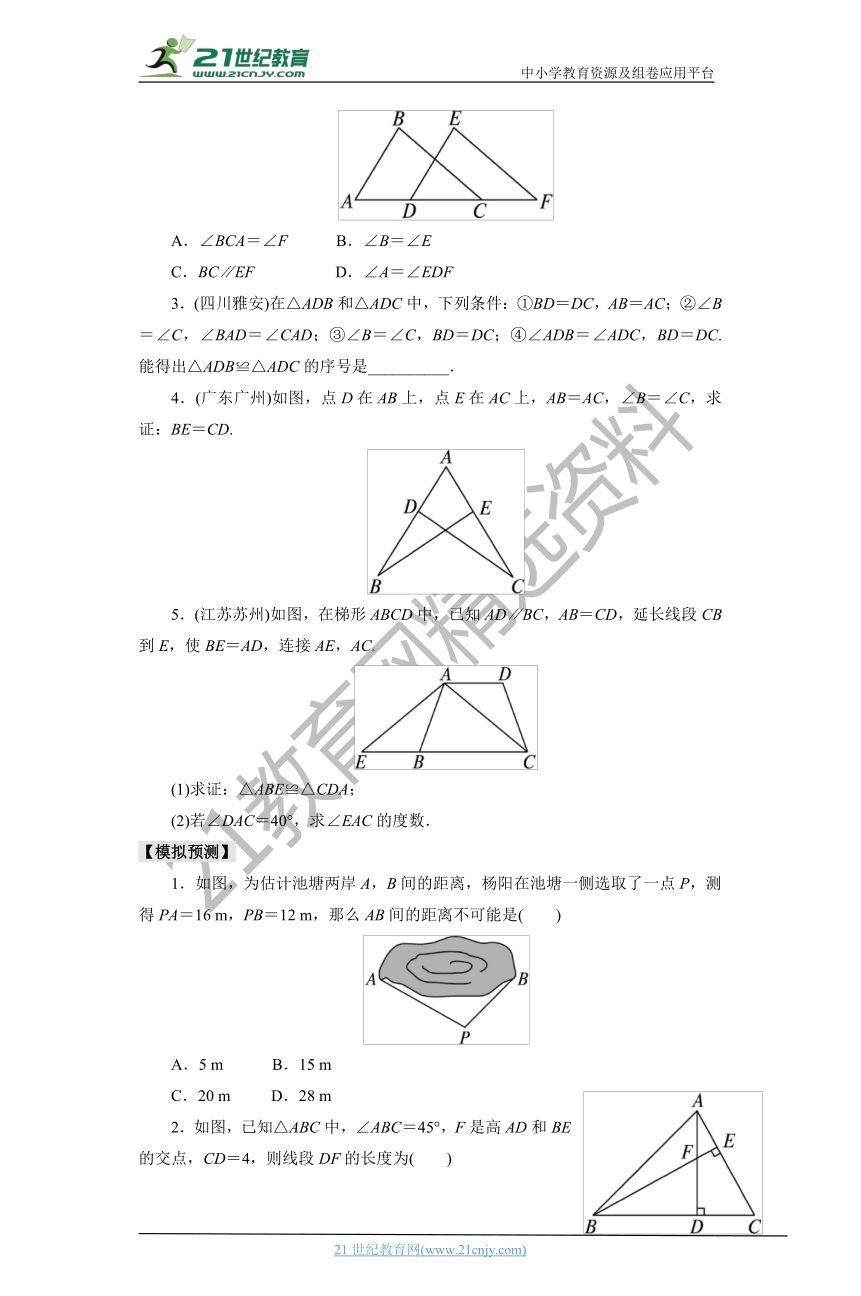
2.(贵阳)如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )【来源:21cnj*y.co*m】
A.∠BCA=∠F B.∠B=∠E
C.BC∥EF D.∠A=∠EDF
3.(四川雅安)在△_ADB??????A_DC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是__________.
4.(广东广州)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BE=CD.[来源:学*科*网]
5.(江苏苏州)如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE,AC.
(1)求证:△ABE≌△CDA;
(2)若∠DAC=40°,求∠EAC的度数.
【模拟预测】
1.如图,为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16 m,PB=12 m,那么AB间的距离不可能是( )
A.5 m B.15 m
C.20 m D.28 m
2.如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为( )
A.2 B.4
C.3 D.4
3.如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B=__________.
4.如图,在△ABC_??????BCè?????_动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大,若∠A减少α度,∠B增加β度,∠C增加γ度,则α,β,γ三者之间的等量关系是__________.
5.如图所示,三角形纸_???ABC??????_∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为__________.
6.如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,∠1__________(填“是”或“不是”)∠2的对顶角,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是__________(只需写出一个).【版权所有:21教育】
7.如图,已知在_???ABC??????_∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过点E作AC的垂线,交CD的延长线于点F.求证:AB=FC.
8.如图,点A,B,D,E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.
参考答案
【考点探究】
触类旁通1.B 由三角形三边的关系可得13-2<x<13+2,即11<x<15,∵x为正整数,∴x为12,13,14,故选B.
触类旁通2.证明:∵BE⊥CF于点E,AD⊥CE于点D,
∴∠BEC=∠CDA=90°.
在Rt△BEC中,∠BCE+∠CBE=90°,
在Rt△BCA中,∠BCE+∠ACD=90°,
∴∠CBE=∠ACD.
在△BEC和△CDA中,
∵
∴△BEC≌△CDA.
触类旁通3.①②④
触类旁通4.证明:∵在△ABC中,AD是中线,∴BD=CD.
∵CF⊥AD,BE⊥AE,∴∠CFD=∠BED=90°.
在△BED与△CFD中,
∵∠BED=∠CFD,∠BDE=∠CDF,BD=CD,
∴△BED≌△CFD,∴BE=CF.
【经典考题】
1.A 设∠A=x,则∠B=2x,∠C=x+20°,则x+2x+x+20°=180°,解得x=40°,即∠A=40°.【来源:21·世纪·教育·网】
2.B 由已知可得两个三角形已有两组边对应相等,还需要另一组边对应相等或夹角对应相等,只有B能满足条件.【出处:21教育名师】
3.①②④ 由_é????????AD???_AD,条件①可组成三边对应相等,条件②可组成两角和其中一角的对边对应相等,条件④可组成两边及其夹角对应相等,这三个条件都可得出△ADB≌△ADC,条件③组成的是两边及其一边的对角对应相等,不能得出△ADB≌△ADC.2·1·c·n·j·y
4.证明:∵在△ABE和△ACD中,∠B=∠C,AB=AC,∠A=∠A,∴△ABE≌△ACD(ASA).∴BE=CD.21教育名师原创作品
5.(1)证明:在梯形ABCD中,∵AD∥BC,AB=CD,
∴∠ABE=∠BAD,∠BAD=∠CDA.
∴∠ABE=∠CDA.
在△ABE和△CDA中,
∴△ABE≌△CDA.
(2)解:由(1)得∠AEB=∠CAD,AE=AC,∴∠AEB=∠ACE.
∵∠DAC=40°,∴∠AEB=∠ACE=40°.
∴∠EAC=180°-40°-40°=100°.
【模拟预测】
1.D 由三角形三边关系知16-12<AB<16+12,故选D.
2.B 因为由已知可证明△BDF≌△ADC,所以DF=CD.
3.70° 4.α=β+γ
5.60° ∵∠A+∠B+∠C=180°,∠CDE+∠CED+∠C=180°,
∴∠A+∠B=∠CDE+∠CED.
∴∠A+∠B+∠CDE+∠CED=2(∠A+∠B)=280°.
∵∠1+∠2+∠CDE+∠CED+∠A+∠B=360°,
∴∠1+∠2=360°-280°=80°.
又∵∠1=20°,∴∠2=60°.[来源:Zxxk.Com]
6.不是 ∠B=∠E(答案不唯一)
7.证明:∵FE⊥AC于点E,∠ACB=90°,
∴∠FEC=∠ACB=90°.
∴∠F+∠ECF=90°.
又∵CD⊥AB于点D,
∴∠A+∠ECF=90°.
∴∠A=∠F.
在△ABC和△FCE中,
∴△ABC≌△FCE.∴AB=FC.
8.证明:∵AD=EB,
∴AD-BD=EB-BD,即AB=ED.
又∵BC∥DF,∴∠CBD=∠FDB.
∴∠ABC=∠EDF.
又∵∠C=∠F,
∴△ABC≌△EDF.
∴AC=EF.[来源:学科网ZXXK]
_21?????????è?????(www.21cnjy.com)_
《三角形与全等三角形》考点探究
【考纲要求】
1.了解三角形和全等三角形有关的概念,知道三角形的稳定性,掌握三角形的三边关系.[来源:Zxxk.Com]21世纪教育网版权所有
2.理解三角形内角和定理及推论.
3.理解三角形的角平分线、中线、高的概念及画法和性质.
4.掌握三角形全等的性质与判定,熟练掌握三角形全等的证明.
【考点探究】
考点一、三角形的边角关系
【例1】若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是( )
A.1 B.5 C.7 D.9
解析:设第三边为x,根据三角形三边的关系可得4-3<x<3+4,即1<x<7.
答案:B
方法总结 1.在具体判断时,可用_è???°??????¤??????_段的和与最长的线段进行比较.若这两条线段的和大于最长的那条线段,则这三条线段能组成三角形.否则就不能组成三角形.21cnjy.com
2.三角形边的关系的应用:(1)判定三条线段是否构成三角形;(2)已知两边的长,确定第三边的取值范围;(3)可证明线段之间的不等关系.
触类旁通1 已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A.2 B.3 C.5 D.13
考点二、全等三角形的性质与判定
【例2】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板AED如图放置,使三角板斜边的两个端点分别与A,D重合,连接BE,EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
解:BE=EC,BE⊥EC.证明如下:
∵AC=2AB,点D是AC的中点,∴AB=AD=CD.
∵∠EAD=∠EDA=45°,∴∠EAB=∠EDC=135°.
又∵EA=ED,∴△EAB≌△EDC.∴∠AEB=∠DEC,EB=EC.∴∠BEC=∠AED=90°.∴BE=EC,BE⊥EC.21·cn·jy·com
方法总结 1.判定两个三角形全等时,常用下面的思路:有两角对应相等时找夹边或任一边对应相等;有两边对应相等时找夹角或另一边对应相等.在具体的证明中,要根据已知条件灵活选择证明方法.www.21-cn-jy.com
2.全等三角形的性质主要是指全等三角形的对应边、对应角、对应中线、对应高、对应角平分线、周长、面积等之间的等量关系.21·世纪*教育网
触类旁通2 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.www-2-1-cnjy-com
求证:△BEC≌△CDA.
考点三、真假命题的判断
【例3】下列命题,正确的是( )
A.如果|a|=|b|,那么a=b
B.等腰梯形的对角线互相垂直
C.顺次连接四边形各边中点所得到的四边形是平行四边形
D.相等的圆周角所对的弧相等[来源:学科网ZXXK]
解析:A项错误,例_??????|???2|_=|2|,但-2≠2;B项错误,等腰梯形的对角线可能垂直,但并不是所有的等腰梯形对角线都垂直;C项正确,可以根据三角形中位线定理和平行四边形的判定得到;D项错误,相等的圆周角所对的弧相等,必须是在同圆或等圆中.21*cnjy*com
答案:C
方法总结 对命题的正确性理解一定要准确,判定命题不成立时,有时可以举反例说明道理;命题有正、误,错误的命题也是命题.2-1-c-n-j-y
触类旁通3 已_??????????????????_直线a,b,c在同一平面内,下列四个命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.其中为真命题的是__________.(填写所有真命题的序号)21*cnjy*com
考点四、证明的方法
【例4】如图,已知在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.
求证:(1)△BFC≌△DFC;
(2)AD=DE.
证明:(1)∵CF平分∠BCD,∴∠BCF=∠DCF.
在△BFC和△DFC中,
∴△BFC≌△DFC.
(2)如图,连接BD.
∵△BFC≌△DFC,
∴BF=DF.∴∠FBD=∠FDB.
∵DF∥AB,∴∠ABD=∠FDB.
∴∠ABD=∠FBD.
∵AD∥BC,∴∠BDA=∠DBC.
∵BC=DC,∴∠DBC=∠BDC.
∴∠BDA=∠BDC.
又BD是公共边,∴△BAD≌△BED.∴AD=DE.
方法总结 1.证明问题时,首先要理清证明的思路,做到证明过程的每一步都有理有据,推理严密.要证明线段、角相等时,证全等是常用的方法.
2.证明的基本方法:(1)综合法,从已知条件入手,探索解题途径的方法;
(2)分析法,从结论出发,用倒推来寻求证题思路的方法;
(3)两头“凑”的方法,综合应用以上两种方法找证明思路的方法.
触类旁通4 如图,在△ABC中,AD是中线,分别过点B,C作AD及其延长线的垂线BE,CF,垂足分别为点E,F.求证:BE=CF.21教育网
【经典考题】
1.(浙江嘉兴)已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
A.40° B.60° C.80° D.90°
2.(贵阳)如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )【来源:21cnj*y.co*m】
A.∠BCA=∠F B.∠B=∠E
C.BC∥EF D.∠A=∠EDF
3.(四川雅安)在△_ADB??????A_DC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是__________.
4.(广东广州)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BE=CD.[来源:学*科*网]
5.(江苏苏州)如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE,AC.
(1)求证:△ABE≌△CDA;
(2)若∠DAC=40°,求∠EAC的度数.
【模拟预测】
1.如图,为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16 m,PB=12 m,那么AB间的距离不可能是( )
A.5 m B.15 m
C.20 m D.28 m
2.如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为( )
A.2 B.4
C.3 D.4
3.如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B=__________.
4.如图,在△ABC_??????BCè?????_动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大,若∠A减少α度,∠B增加β度,∠C增加γ度,则α,β,γ三者之间的等量关系是__________.
5.如图所示,三角形纸_???ABC??????_∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为__________.
6.如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,∠1__________(填“是”或“不是”)∠2的对顶角,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是__________(只需写出一个).【版权所有:21教育】
7.如图,已知在_???ABC??????_∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过点E作AC的垂线,交CD的延长线于点F.求证:AB=FC.
8.如图,点A,B,D,E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.
参考答案
【考点探究】
触类旁通1.B 由三角形三边的关系可得13-2<x<13+2,即11<x<15,∵x为正整数,∴x为12,13,14,故选B.
触类旁通2.证明:∵BE⊥CF于点E,AD⊥CE于点D,
∴∠BEC=∠CDA=90°.
在Rt△BEC中,∠BCE+∠CBE=90°,
在Rt△BCA中,∠BCE+∠ACD=90°,
∴∠CBE=∠ACD.
在△BEC和△CDA中,
∵
∴△BEC≌△CDA.
触类旁通3.①②④
触类旁通4.证明:∵在△ABC中,AD是中线,∴BD=CD.
∵CF⊥AD,BE⊥AE,∴∠CFD=∠BED=90°.
在△BED与△CFD中,
∵∠BED=∠CFD,∠BDE=∠CDF,BD=CD,
∴△BED≌△CFD,∴BE=CF.
【经典考题】
1.A 设∠A=x,则∠B=2x,∠C=x+20°,则x+2x+x+20°=180°,解得x=40°,即∠A=40°.【来源:21·世纪·教育·网】
2.B 由已知可得两个三角形已有两组边对应相等,还需要另一组边对应相等或夹角对应相等,只有B能满足条件.【出处:21教育名师】
3.①②④ 由_é????????AD???_AD,条件①可组成三边对应相等,条件②可组成两角和其中一角的对边对应相等,条件④可组成两边及其夹角对应相等,这三个条件都可得出△ADB≌△ADC,条件③组成的是两边及其一边的对角对应相等,不能得出△ADB≌△ADC.2·1·c·n·j·y
4.证明:∵在△ABE和△ACD中,∠B=∠C,AB=AC,∠A=∠A,∴△ABE≌△ACD(ASA).∴BE=CD.21教育名师原创作品
5.(1)证明:在梯形ABCD中,∵AD∥BC,AB=CD,
∴∠ABE=∠BAD,∠BAD=∠CDA.
∴∠ABE=∠CDA.
在△ABE和△CDA中,
∴△ABE≌△CDA.
(2)解:由(1)得∠AEB=∠CAD,AE=AC,∴∠AEB=∠ACE.
∵∠DAC=40°,∴∠AEB=∠ACE=40°.
∴∠EAC=180°-40°-40°=100°.
【模拟预测】
1.D 由三角形三边关系知16-12<AB<16+12,故选D.
2.B 因为由已知可证明△BDF≌△ADC,所以DF=CD.
3.70° 4.α=β+γ
5.60° ∵∠A+∠B+∠C=180°,∠CDE+∠CED+∠C=180°,
∴∠A+∠B=∠CDE+∠CED.
∴∠A+∠B+∠CDE+∠CED=2(∠A+∠B)=280°.
∵∠1+∠2+∠CDE+∠CED+∠A+∠B=360°,
∴∠1+∠2=360°-280°=80°.
又∵∠1=20°,∴∠2=60°.[来源:Zxxk.Com]
6.不是 ∠B=∠E(答案不唯一)
7.证明:∵FE⊥AC于点E,∠ACB=90°,
∴∠FEC=∠ACB=90°.
∴∠F+∠ECF=90°.
又∵CD⊥AB于点D,
∴∠A+∠ECF=90°.
∴∠A=∠F.
在△ABC和△FCE中,
∴△ABC≌△FCE.∴AB=FC.
8.证明:∵AD=EB,
∴AD-BD=EB-BD,即AB=ED.
又∵BC∥DF,∴∠CBD=∠FDB.
∴∠ABC=∠EDF.
又∵∠C=∠F,
∴△ABC≌△EDF.
∴AC=EF.[来源:学科网ZXXK]
_21?????????è?????(www.21cnjy.com)_
同课章节目录
