人教版六年级上册数学3分数除法——解决问题(4) 课件(24页ppt)
文档属性
| 名称 | 人教版六年级上册数学3分数除法——解决问题(4) 课件(24页ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 16:09:42 | ||
图片预览








文档简介
(共24张PPT)
分数除法
3
人教版·六年级上册
第8课时 解决问题(3)
1.修一条360米的公路,甲队修12天完成,平均每天( )米。
2.修一条360米的公路,甲队每天修18米,( )天能完成。
一、新课引入
填一填。
30
20
以上问题涉及到了哪个知识点?那它们的关系又如何呢?
工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
二、例题讲解
如果两队合修,多少天能修完?
7
阅读与理解
已知条件 所求问题
一队单独修要12天完成
二队单独修要18天完成
两队合修,多少天能修完
这条道路,如果我们一队单独修,12天能修完。
如果我们二队单独修,18 天才能修完。
要解决“两队合修,多少天修完?”这个问题,需要知道哪些信息?
如果知道了这两个信息,这个问题可以怎样解决?
这条路的长度—“工作总量”;两队 1 天各修的长度 —“工作效率”。
这条路的长度÷(一队 1 天修的长度 + 二队 1 天修的长度)
阅读与理解
二、例题讲解
可是这条道路有多长呢?
二、新课讲解
分析与解答
能不能假设知道这条路有多长呢?
我假设这条道路长18km。
一队每天修多少千米:
。
二队每天修多少千米:
两队合修,每天修多少千米:
两队合修,需要多少天:
3
2
18÷12= (km)
18÷18=1(km)
3
2
5
2
+ 1= (km)
5
2
18÷ =7.2(天)
二、新课讲解
分析与解答
能不能假设知道这条路有多长呢?
我假设这条道路长30km。
一队每天修多少千米:
。
二队每天修多少千米:
两队合修,每天修多少千米:
两队合修,需要多少天:
5
2
30÷12= (km)
30÷18= (km)
5
3
5
2
5
3
+ = (km)
25
6
30÷ =7.2(天)
25
6
二、新课讲解
分析与解答
能不能假设知道这条路有多长呢?
我假设这条道路长1km。
那两个队每天修的长度分别是 。
不同的方法计算出的结果一样吗?
回顾与反思
二、新课讲解
怎样才知道以上的解决方法是否正确?把你的想法写下来,和同学交流一下。
分别求出一队和二队7.2天修的道路,再将它们合起来,看一看够不够单位“1”。
不管假设这条道路有多长,答案都是相同的。把道路长度假设成1,很简便。
答:如果两队合修,7.2天可以修完。
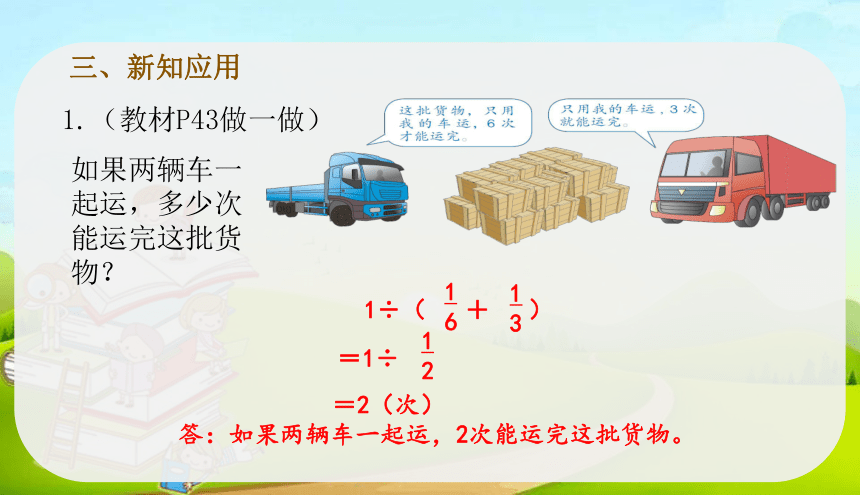
三、新知应用
如果两辆车一起运,多少次能运完这批货物?
1.(教材P43做一做)
1÷( + )
=1÷
=2(次)
1
3
1
6
1
2
答:如果两辆车一起运,2次能运完这批货物。
2.(教材P45第6题) 挖一条水渠,王伯伯每天挖整条水的 ,李叔叔每天挖整条水渠的 。两人合作,几天能挖完?
三、新知应用
答:12天能挖完。
1÷( + )
=1÷
=12(天)
1
20
1
30
5
60
回顾本节课的学习,你有哪些收获呢?
四、课堂小结
工程问题
将工作总量看作单位“1”,用单位时间内完成工作总量的几分之一表示工作效率。
基本等量关系式:
工作总量÷工作效率之和=工作时间
巩固练习
1.水族箱里有红、黑两种金鱼共18条。其中黑金鱼的条数是红金鱼的 。红金鱼和黑金鱼各有多少条?
知识点1
一、复习巩固
1
5
答:红金鱼有15条,黑金鱼有3条。
解决含有两个未知量的分数应用题
x = 15
x(1+ )
= 18
×15 = 3(条)
x
= 18÷
1
5
6
5
1
5
解:设红金鱼有x条,黑金鱼有 x条。
1
5
2.(教材P44第3题)航模小组和美术小组分别有多少人?
解:设航模小组有为x 人,则美术小组有 x 人。
x + x = 45
x = 45
x = 25 25× =20(人)
4
5
4
5
9
5
4
5
答:航模小组有25人,美术小组有20人。
基础练习
航模小组和美术小组一共有45人。美术小组的人数是航模小组的
解决含有两个未知量的分数应用题
知识总结
有两个量都是未知的,先把谁看作单位“1”都可以,设其中一个量为未知数x,用这个量表示另一个量,然后找出等量关系,列方程解答出一个量,再解答第二个量。
3.一项工程,甲独做5天完成,乙独做4天完成,甲乙合做需要多少天完成?
知识点2
一、复习巩固
工 程 问 题
1÷( + )
=1÷
= (天)
1
5
1
4
9
20
20
9
答:甲乙合做需要 天。
20
9
4.(教材P45第7题)甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市到B城市出发,几小时后相遇?
1÷( + )
=1÷
=
1
2
1
3
5
6
6
5
答: 小时后相遇。
6
5
基础练习
(1)把工作总量看作单位“1”。
(2)解决工程问题的关键是用单位时间内完成工作总量的几分之一来表示工作效率
(3)工作总量÷工作效率之和=工作时间
知识总结
工 程 问 题
二、课堂练习
1.(教材P45第5题)中国农历中的“夏至”是一年中白昼最长、黑夜最短的一天。这一天,北京的黑夜时间是白天时间的 。白昼和黑夜分别是多少小时?
3
5
一天一共有24个小时,也就是白昼+黑夜=24小时。
解:设白昼的时间是x 小时,黑夜的时间是 x 小时。
3
5
x + x = 24
x = 24
x = 15
15 × =9(小时)
3
5
8
5
3
5
答:白昼是15小时,黑夜是9小时。
二、课堂练习
2.(教材P45第8题)某地遭遇暴雨,水库水位已经超过警戒线,急需泄洪。这个水库有两个泄洪口。只打开A口,8小时完成任务,只打开B口,6小时可以完成任务。如果两泄洪口同时打开,几小时可以完成任务?
1÷( + )
=1÷
= (小时)
1
8
1
10
9
40
40
9
答: 可以完成任务。
24
7
二、课堂练习
3.(教材P45第9题)现在两队合种,5天能种完吗?
1÷( + )
=1÷
= (天)
1
8
1
10
9
40
40
9
40
9
< 5
答:两队合种,5天能种完。
一共有300棵树。如果一队单独种,需要8天。如果二队单独种,需要10天。
三、拓展提升
一项工程,甲队单独做需要10天完成,乙队单独做需要12天完成,丙队单独做需要15天完成,甲队先做2天剩下的乙丙合作几天可以完成?
(1- ÷( + )
= ÷
= (天)
1
15
1
12
9
60
16
3
1
10
4
5
×2)
答:甲队先做2天剩下的乙丙合作 天可以完成。
16
3
五、课后作业
完成课本“练习九”第45页第7、8、9题。
聪明出于勤奋,天才在于积累。
分数除法
3
人教版·六年级上册
第8课时 解决问题(3)
1.修一条360米的公路,甲队修12天完成,平均每天( )米。
2.修一条360米的公路,甲队每天修18米,( )天能完成。
一、新课引入
填一填。
30
20
以上问题涉及到了哪个知识点?那它们的关系又如何呢?
工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
二、例题讲解
如果两队合修,多少天能修完?
7
阅读与理解
已知条件 所求问题
一队单独修要12天完成
二队单独修要18天完成
两队合修,多少天能修完
这条道路,如果我们一队单独修,12天能修完。
如果我们二队单独修,18 天才能修完。
要解决“两队合修,多少天修完?”这个问题,需要知道哪些信息?
如果知道了这两个信息,这个问题可以怎样解决?
这条路的长度—“工作总量”;两队 1 天各修的长度 —“工作效率”。
这条路的长度÷(一队 1 天修的长度 + 二队 1 天修的长度)
阅读与理解
二、例题讲解
可是这条道路有多长呢?
二、新课讲解
分析与解答
能不能假设知道这条路有多长呢?
我假设这条道路长18km。
一队每天修多少千米:
。
二队每天修多少千米:
两队合修,每天修多少千米:
两队合修,需要多少天:
3
2
18÷12= (km)
18÷18=1(km)
3
2
5
2
+ 1= (km)
5
2
18÷ =7.2(天)
二、新课讲解
分析与解答
能不能假设知道这条路有多长呢?
我假设这条道路长30km。
一队每天修多少千米:
。
二队每天修多少千米:
两队合修,每天修多少千米:
两队合修,需要多少天:
5
2
30÷12= (km)
30÷18= (km)
5
3
5
2
5
3
+ = (km)
25
6
30÷ =7.2(天)
25
6
二、新课讲解
分析与解答
能不能假设知道这条路有多长呢?
我假设这条道路长1km。
那两个队每天修的长度分别是 。
不同的方法计算出的结果一样吗?
回顾与反思
二、新课讲解
怎样才知道以上的解决方法是否正确?把你的想法写下来,和同学交流一下。
分别求出一队和二队7.2天修的道路,再将它们合起来,看一看够不够单位“1”。
不管假设这条道路有多长,答案都是相同的。把道路长度假设成1,很简便。
答:如果两队合修,7.2天可以修完。
三、新知应用
如果两辆车一起运,多少次能运完这批货物?
1.(教材P43做一做)
1÷( + )
=1÷
=2(次)
1
3
1
6
1
2
答:如果两辆车一起运,2次能运完这批货物。
2.(教材P45第6题) 挖一条水渠,王伯伯每天挖整条水的 ,李叔叔每天挖整条水渠的 。两人合作,几天能挖完?
三、新知应用
答:12天能挖完。
1÷( + )
=1÷
=12(天)
1
20
1
30
5
60
回顾本节课的学习,你有哪些收获呢?
四、课堂小结
工程问题
将工作总量看作单位“1”,用单位时间内完成工作总量的几分之一表示工作效率。
基本等量关系式:
工作总量÷工作效率之和=工作时间
巩固练习
1.水族箱里有红、黑两种金鱼共18条。其中黑金鱼的条数是红金鱼的 。红金鱼和黑金鱼各有多少条?
知识点1
一、复习巩固
1
5
答:红金鱼有15条,黑金鱼有3条。
解决含有两个未知量的分数应用题
x = 15
x(1+ )
= 18
×15 = 3(条)
x
= 18÷
1
5
6
5
1
5
解:设红金鱼有x条,黑金鱼有 x条。
1
5
2.(教材P44第3题)航模小组和美术小组分别有多少人?
解:设航模小组有为x 人,则美术小组有 x 人。
x + x = 45
x = 45
x = 25 25× =20(人)
4
5
4
5
9
5
4
5
答:航模小组有25人,美术小组有20人。
基础练习
航模小组和美术小组一共有45人。美术小组的人数是航模小组的
解决含有两个未知量的分数应用题
知识总结
有两个量都是未知的,先把谁看作单位“1”都可以,设其中一个量为未知数x,用这个量表示另一个量,然后找出等量关系,列方程解答出一个量,再解答第二个量。
3.一项工程,甲独做5天完成,乙独做4天完成,甲乙合做需要多少天完成?
知识点2
一、复习巩固
工 程 问 题
1÷( + )
=1÷
= (天)
1
5
1
4
9
20
20
9
答:甲乙合做需要 天。
20
9
4.(教材P45第7题)甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市到B城市出发,几小时后相遇?
1÷( + )
=1÷
=
1
2
1
3
5
6
6
5
答: 小时后相遇。
6
5
基础练习
(1)把工作总量看作单位“1”。
(2)解决工程问题的关键是用单位时间内完成工作总量的几分之一来表示工作效率
(3)工作总量÷工作效率之和=工作时间
知识总结
工 程 问 题
二、课堂练习
1.(教材P45第5题)中国农历中的“夏至”是一年中白昼最长、黑夜最短的一天。这一天,北京的黑夜时间是白天时间的 。白昼和黑夜分别是多少小时?
3
5
一天一共有24个小时,也就是白昼+黑夜=24小时。
解:设白昼的时间是x 小时,黑夜的时间是 x 小时。
3
5
x + x = 24
x = 24
x = 15
15 × =9(小时)
3
5
8
5
3
5
答:白昼是15小时,黑夜是9小时。
二、课堂练习
2.(教材P45第8题)某地遭遇暴雨,水库水位已经超过警戒线,急需泄洪。这个水库有两个泄洪口。只打开A口,8小时完成任务,只打开B口,6小时可以完成任务。如果两泄洪口同时打开,几小时可以完成任务?
1÷( + )
=1÷
= (小时)
1
8
1
10
9
40
40
9
答: 可以完成任务。
24
7
二、课堂练习
3.(教材P45第9题)现在两队合种,5天能种完吗?
1÷( + )
=1÷
= (天)
1
8
1
10
9
40
40
9
40
9
< 5
答:两队合种,5天能种完。
一共有300棵树。如果一队单独种,需要8天。如果二队单独种,需要10天。
三、拓展提升
一项工程,甲队单独做需要10天完成,乙队单独做需要12天完成,丙队单独做需要15天完成,甲队先做2天剩下的乙丙合作几天可以完成?
(1- ÷( + )
= ÷
= (天)
1
15
1
12
9
60
16
3
1
10
4
5
×2)
答:甲队先做2天剩下的乙丙合作 天可以完成。
16
3
五、课后作业
完成课本“练习九”第45页第7、8、9题。
聪明出于勤奋,天才在于积累。
