人教版数学六年级上册5.2圆的周长课件(27张ppt)
文档属性
| 名称 | 人教版数学六年级上册5.2圆的周长课件(27张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 19:34:24 | ||
图片预览




文档简介
(共27张PPT)
圆
1
人教版·六年级上册
第3课时 圆的周长
一、新课引入
同学们,你们有办法解决吗?
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
同学们,你们有办法解决吗?
分别需要多长的铁皮啊?
分别需要多长的铁皮啊?
0
1
2
3
4
6
7
8
5
A
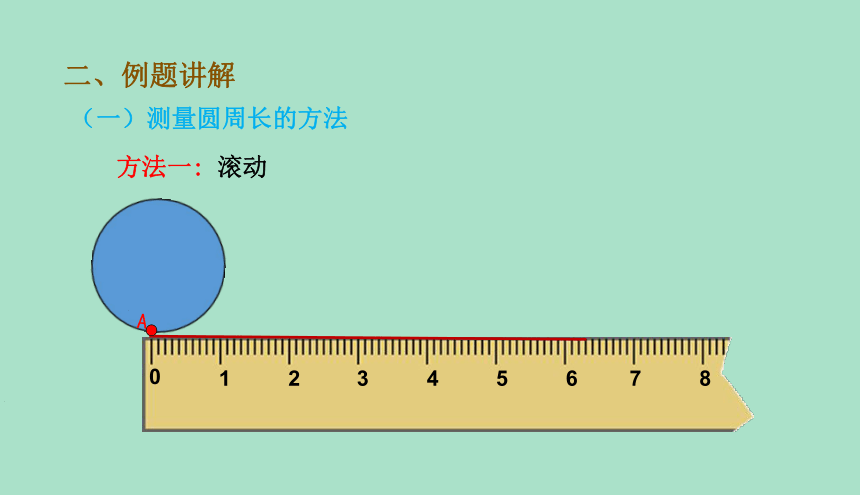
方法一: 滚动
A
A
二、例题讲解
(一)测量圆周长的方法
A
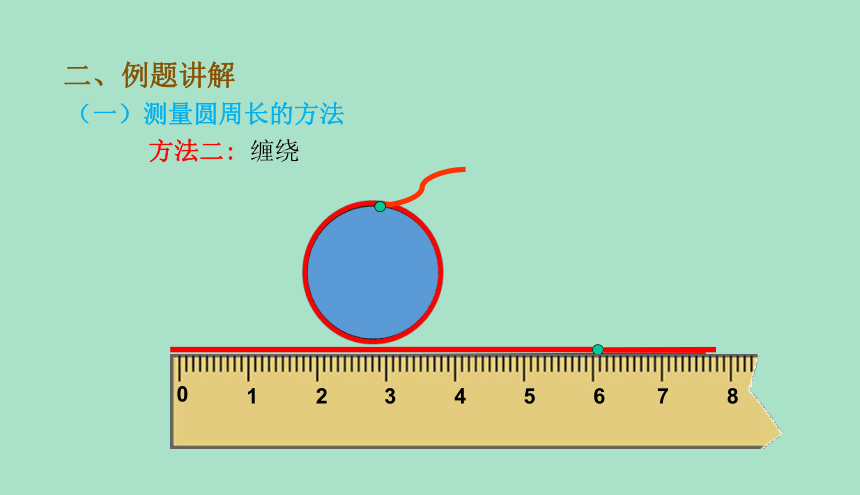
方法二: 缠绕
二、例题讲解
(一)测量圆周长的方法
0
1
2
3
4
6
7
8
5
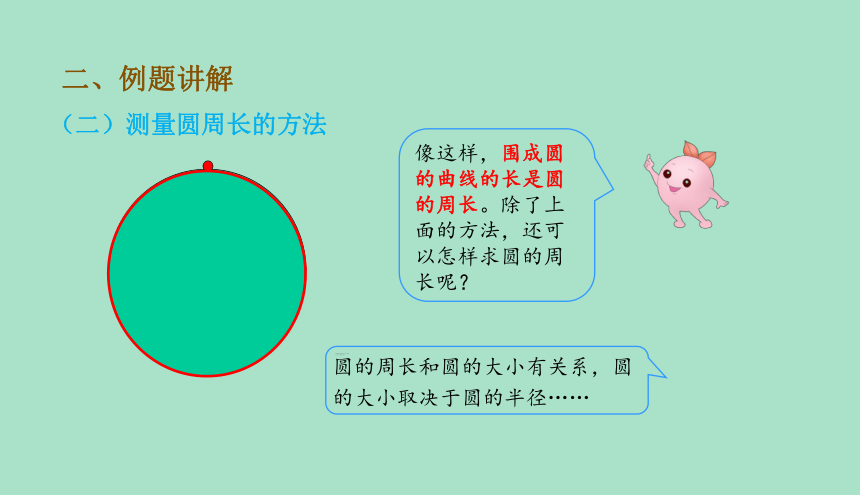
圆的周长和圆的大小有关系,圆的
大小取决于圆的半径……
像这样,围成圆的曲线的长是圆的周长。除了上面的方法,还可以怎样求圆的周长呢?
圆的周长和圆的大小有关系,圆的大小取决于圆的半径……
二、例题讲解
(二)测量圆周长的方法
二、例题讲解
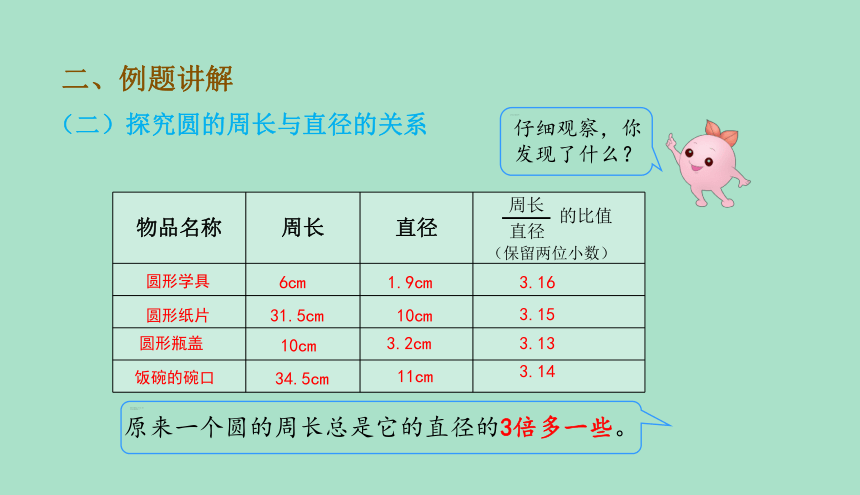
(二)探究圆的周长与直径的关系
让我们来做一个实验:找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入表中,看看有什么发现。
圆的周长和圆的大小有关系,圆的
大小取决于圆的半径……
二、例题讲解
(二)探究圆的周长与直径的关系
物品名称 周长 直径
直径
的比值
周长
(保留两位小数)
圆形学具
圆形纸片
圆形瓶盖
饭碗的碗口
6cm
31.5cm
10cm
34.5cm
1.9cm
10cm
3.2cm
11cm
3.16
3.15
3.13
3.14
原来一个圆的周长总是它的直径的3倍多一些。
分别需要多长的铁皮啊?
仔细观察,你发现了什么?
其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π(pài)表示。它是一个无限不循环小数,π=3.1415926535…但在实际应用中常常只取它的近似值,例如 π ≈ 3.14。
二、例题讲解
(三)探究圆的周长的计算公式
二、例题讲解
(三)探究圆的周长的计算公式
圆的周长 =
圆的周长总是直径的 π 倍。
直径 × 圆周率
例1. 这辆自行车轮子转一圈,大约可以走多远?(结果保留正米数)小明家离学校 1 km,骑车从家到学校,轮子大约转了多少圈?
2×3.14×33=207.24(cm)≈ 2(m)
1000÷2 ≈500(圈)
1 km=1000 m
答:这辆自行车轮子转一圈,大约可以走 2 m。
小明从家到学校,轮子大约转了 500 圈。
这辆自行车轮子的半径大约是 33 cm。
二、例题讲解
三、新知运用
1.(教材P64做一做第1题)计算下面圆的周长。
C=2πr
=2×3.14×3
=18.84(c㎡)
C=πd
=3.14×6
=18.84(c㎡)
C=2πr
=2×3.14×5
=31.4(c㎡)
4.71÷3.14=1.5(m)
答:这个圆桌面的直径是1.5 m。
2. (教材P64做一做第1题)这个圆桌面的直径是多少?
我用卷尺量得圆桌面的周长是4.71 m。
C=πd
d=C÷π
三、新知运用
四、课堂小结
回顾本节课,你学会了什么?
1.一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π(pài)表示,它是一个无限不循环小数,π=3.1415926535…但在实际应用中常常只取它的近似值,例如 π≈3.14。
C=πd 或 C=2πr
2.如果用C表示圆的周长,就有:
巩固训练
1. 一个圆形喷水池的半径是5m,它的周长是多少米?
2×3.14×5=31.4(米)
答:它的周长是31.4米。
圆的周长C=2πr
圆的周长
知识点1
一、复习巩固
(教材P65第1题)
2. 在一个圆形亭子里,小丽沿着直径从一端走12步到达另一端,每步长大约是55cm。这个圆的周长大约是多少米?
3.14×(55×12)=2072.4(cm)
2072.4cm=20.724m
答:这个圆的周长大约是20.724米。
求出直径就可以求出周长
基础练习
一、复习巩固
(教材P65第2题)
3. 小红量得一个古代建筑中的大红圆柱的周长是
3.77m。这个圆柱的直径是多少米?(得数保留一位小数。)
3.77÷3.14≈1.2(米)
答:这个圆柱的直径约1.2米。
C = πd
d = C÷π
基础练习
一、复习巩固
(教材P65第3题)
一、复习巩固
C = πd
C = 2πr
求周长:
知道直径:
知道半径:
d = 2r
求直径:
知道半径:
知道周长:
d = C÷π
r = d÷2
求半径:
知道直径:
知道周长:
r = C÷π÷2
知识总结
二、课堂练习
1. 一只挂钟的分针长20cm,经过30分钟后,分针的尖端所走的路程是多少厘米?经过45分钟呢?
2×3.14×20× =62.8(cm)
30
60
2×3.14×20× =94.2(cm)
45
60
答:经过30分钟后分针的尖端所走的路程是62.8cm。
经过45分钟后分针的尖端所走的路程是94.2cm。
分针的长度就是圆的半径。
分针的尖端走30分钟就是圆周长的一半。
走45分钟就是圆周长的
45
60
(教材P65第4题)
二、课堂练习
2. 一个圆形牛栏的半径是15m,要用多长的粗铁丝才能把牛栏围上3圈?(接头处忽略不计。)如果每隔2m打一根木桩,大约要打多少根木桩?
15×2×3.14×3=282.6(m)
答:要用282.6m长的铁丝才能把牛栏围上3圈。
15×2×3.14÷2≈47(根)
答:大约要打47根木桩。
(教材P65第5题)
二、课堂练习
4. 看图填空(单位:cm)。
(1)
(2)
正方形的周长是( )cm,圆的周长是( )cm。
其中一个圆的周长是( )cm,长方形的周长是( )cm。
16
12.56
9.42
21
r=2cm
r=1.5cm
(教材P66第7题)
二、课堂练习
5. 在一个周长为100cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是多少厘米?
100÷4× =12.5(厘米)
1
2
答:这个圆的半径是12.5厘米。
正方形的边长就是圆的直径。
(教材P66第8题)
二、课堂练习
6. 李明家一扇门上要装上形状如右图所示的装饰木条,需要木条多少米?
50×3.14× =78.5(cm)
1
2
50×4=200(cm)
200+78.5=278.5(cm)
278.5cm=2.785m
答:需要木条2.785m。
d=50cm
50cm
50cm
(教材P66第9题)
二、课堂练习
7. 下面图形的周长是多少厘米?你是怎样算的?
2×3.14×5÷2+3.14×5=31.4(厘米)
答:周长是31.4厘米。
5cm
它的周长就是一个大半圆和两个小半圆的长度。
(教材P66第10题)
1. 把圆柱形物体分别捆成如下图(从底面方向看)的形状,如果接头处不计,每组至少需要多长的绳子?你发现了什么?
第一幅图:7×2+3.14×7=35.98(cm)
第二幅图:7×4+3.14×7=49.98(cm)
第三幅图:7×8+3.14×7=77.98(cm)
7cm
(教材P66第11题)
五、课后作业
完成课本“练习十四”第65页第1题、第3题。
聪明出于勤奋,天才在于积累。
圆
1
人教版·六年级上册
第3课时 圆的周长
一、新课引入
同学们,你们有办法解决吗?
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
同学们,你们有办法解决吗?
分别需要多长的铁皮啊?
分别需要多长的铁皮啊?
0
1
2
3
4
6
7
8
5
A
方法一: 滚动
A
A
二、例题讲解
(一)测量圆周长的方法
A
方法二: 缠绕
二、例题讲解
(一)测量圆周长的方法
0
1
2
3
4
6
7
8
5
圆的周长和圆的大小有关系,圆的
大小取决于圆的半径……
像这样,围成圆的曲线的长是圆的周长。除了上面的方法,还可以怎样求圆的周长呢?
圆的周长和圆的大小有关系,圆的大小取决于圆的半径……
二、例题讲解
(二)测量圆周长的方法
二、例题讲解
(二)探究圆的周长与直径的关系
让我们来做一个实验:找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入表中,看看有什么发现。
圆的周长和圆的大小有关系,圆的
大小取决于圆的半径……
二、例题讲解
(二)探究圆的周长与直径的关系
物品名称 周长 直径
直径
的比值
周长
(保留两位小数)
圆形学具
圆形纸片
圆形瓶盖
饭碗的碗口
6cm
31.5cm
10cm
34.5cm
1.9cm
10cm
3.2cm
11cm
3.16
3.15
3.13
3.14
原来一个圆的周长总是它的直径的3倍多一些。
分别需要多长的铁皮啊?
仔细观察,你发现了什么?
其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π(pài)表示。它是一个无限不循环小数,π=3.1415926535…但在实际应用中常常只取它的近似值,例如 π ≈ 3.14。
二、例题讲解
(三)探究圆的周长的计算公式
二、例题讲解
(三)探究圆的周长的计算公式
圆的周长 =
圆的周长总是直径的 π 倍。
直径 × 圆周率
例1. 这辆自行车轮子转一圈,大约可以走多远?(结果保留正米数)小明家离学校 1 km,骑车从家到学校,轮子大约转了多少圈?
2×3.14×33=207.24(cm)≈ 2(m)
1000÷2 ≈500(圈)
1 km=1000 m
答:这辆自行车轮子转一圈,大约可以走 2 m。
小明从家到学校,轮子大约转了 500 圈。
这辆自行车轮子的半径大约是 33 cm。
二、例题讲解
三、新知运用
1.(教材P64做一做第1题)计算下面圆的周长。
C=2πr
=2×3.14×3
=18.84(c㎡)
C=πd
=3.14×6
=18.84(c㎡)
C=2πr
=2×3.14×5
=31.4(c㎡)
4.71÷3.14=1.5(m)
答:这个圆桌面的直径是1.5 m。
2. (教材P64做一做第1题)这个圆桌面的直径是多少?
我用卷尺量得圆桌面的周长是4.71 m。
C=πd
d=C÷π
三、新知运用
四、课堂小结
回顾本节课,你学会了什么?
1.一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π(pài)表示,它是一个无限不循环小数,π=3.1415926535…但在实际应用中常常只取它的近似值,例如 π≈3.14。
C=πd 或 C=2πr
2.如果用C表示圆的周长,就有:
巩固训练
1. 一个圆形喷水池的半径是5m,它的周长是多少米?
2×3.14×5=31.4(米)
答:它的周长是31.4米。
圆的周长C=2πr
圆的周长
知识点1
一、复习巩固
(教材P65第1题)
2. 在一个圆形亭子里,小丽沿着直径从一端走12步到达另一端,每步长大约是55cm。这个圆的周长大约是多少米?
3.14×(55×12)=2072.4(cm)
2072.4cm=20.724m
答:这个圆的周长大约是20.724米。
求出直径就可以求出周长
基础练习
一、复习巩固
(教材P65第2题)
3. 小红量得一个古代建筑中的大红圆柱的周长是
3.77m。这个圆柱的直径是多少米?(得数保留一位小数。)
3.77÷3.14≈1.2(米)
答:这个圆柱的直径约1.2米。
C = πd
d = C÷π
基础练习
一、复习巩固
(教材P65第3题)
一、复习巩固
C = πd
C = 2πr
求周长:
知道直径:
知道半径:
d = 2r
求直径:
知道半径:
知道周长:
d = C÷π
r = d÷2
求半径:
知道直径:
知道周长:
r = C÷π÷2
知识总结
二、课堂练习
1. 一只挂钟的分针长20cm,经过30分钟后,分针的尖端所走的路程是多少厘米?经过45分钟呢?
2×3.14×20× =62.8(cm)
30
60
2×3.14×20× =94.2(cm)
45
60
答:经过30分钟后分针的尖端所走的路程是62.8cm。
经过45分钟后分针的尖端所走的路程是94.2cm。
分针的长度就是圆的半径。
分针的尖端走30分钟就是圆周长的一半。
走45分钟就是圆周长的
45
60
(教材P65第4题)
二、课堂练习
2. 一个圆形牛栏的半径是15m,要用多长的粗铁丝才能把牛栏围上3圈?(接头处忽略不计。)如果每隔2m打一根木桩,大约要打多少根木桩?
15×2×3.14×3=282.6(m)
答:要用282.6m长的铁丝才能把牛栏围上3圈。
15×2×3.14÷2≈47(根)
答:大约要打47根木桩。
(教材P65第5题)
二、课堂练习
4. 看图填空(单位:cm)。
(1)
(2)
正方形的周长是( )cm,圆的周长是( )cm。
其中一个圆的周长是( )cm,长方形的周长是( )cm。
16
12.56
9.42
21
r=2cm
r=1.5cm
(教材P66第7题)
二、课堂练习
5. 在一个周长为100cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是多少厘米?
100÷4× =12.5(厘米)
1
2
答:这个圆的半径是12.5厘米。
正方形的边长就是圆的直径。
(教材P66第8题)
二、课堂练习
6. 李明家一扇门上要装上形状如右图所示的装饰木条,需要木条多少米?
50×3.14× =78.5(cm)
1
2
50×4=200(cm)
200+78.5=278.5(cm)
278.5cm=2.785m
答:需要木条2.785m。
d=50cm
50cm
50cm
(教材P66第9题)
二、课堂练习
7. 下面图形的周长是多少厘米?你是怎样算的?
2×3.14×5÷2+3.14×5=31.4(厘米)
答:周长是31.4厘米。
5cm
它的周长就是一个大半圆和两个小半圆的长度。
(教材P66第10题)
1. 把圆柱形物体分别捆成如下图(从底面方向看)的形状,如果接头处不计,每组至少需要多长的绳子?你发现了什么?
第一幅图:7×2+3.14×7=35.98(cm)
第二幅图:7×4+3.14×7=49.98(cm)
第三幅图:7×8+3.14×7=77.98(cm)
7cm
(教材P66第11题)
五、课后作业
完成课本“练习十四”第65页第1题、第3题。
聪明出于勤奋,天才在于积累。
