人教版数学六年级上册5.6圆环的面积 (例2、3) 课件(22张ppt)
文档属性
| 名称 | 人教版数学六年级上册5.6圆环的面积 (例2、3) 课件(22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
圆
5
人教版·六年级上册
第6课时 圆环的面积
一、新课引入
1.求出下列图形的面积。
d=6cm
r=2cm
c=12.56
r=d÷2=6÷2=3(cm)
s=πr2
=3.14×32
=28.26(cm2)
s=πr2
=3.14×22
=12.56(cm2)
r=c÷π÷2
=12.56÷3.14÷2
=2(cm)
s=πr2
=3.14×22
=12.56(cm2)
2.画图
一、新课引入
(1)用圆规画一个半径是1cm的圆,并标上圆心0;
(2)圆心相同,再画一个半径是2cm的圆。
0
像这样的图形我们称之为圆环。
二、例题讲解
生活中的圆环。
二、例题讲解
例2:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
怎样利用内圆和外圆的面积求出圆环的面积?
圆环面积=外圆面积–内圆面积
我是这样想的……
二、例题讲解
3.14×6 -3.14×2
=113.04-12.56
=100.48(cm )
3.14×(6 -2 )
=3.14×32
=100.48(cm )
答:圆环的面积是100.48 cm 。
我是这样想的……
还可以这样计算……
例2:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
二、例题讲解
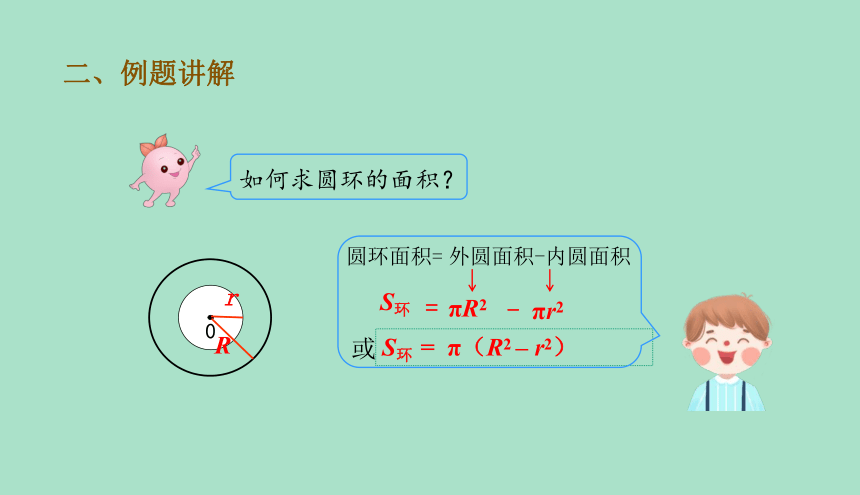
圆环面积=
πR2
- πr2
外圆面积-内圆面积
S环
=
S环 = π(R2 – r2)
或
如何求圆环的面积?
0
r
R
三、新知运用
50÷2=25(m) 10÷2=5(m)
答:草坪的占地面积是1884m 。
1. 一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?(教材P68做一做第2题)
3.14×(25 -5 )
=3.14×600
=1884(m )
要求草坪的占地面积,也就是求圆环的面积。
2.图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。(教材P72第6题)
三、新知运用
6cm
阴影部分的面积=大圆面积—小圆面积
大圆半径等于小圆的直径
R=6cm
r=6÷2=3cm
S=πR2- πr2
= π(R2 – r2)
=3.14×(62–32)
=84.78(cm )
答:阴影部分的面积84.78cm 。
如何计算圆环的面积?
四、课堂小结
圆环面积=
πR2
- πr2
外圆面积-内圆面积
S环
=
S环 = π(R2 – r2)
或
0
r
R
圆
5
人教版·六年级上册
解决问题
一、新课引入
中国建筑和生活中经常能见到“外方内圆”和“外圆内方”的设计。
例3:下图中的两个圆半径都是1m,你能求出正方形和圆之间部分的面积吗?
二、例题讲解
二、例题讲解
题目中都告诉了我们什么数学信息?
上图中两个圆的半径都是 1 m,怎样求正方形和圆之间部分的面积呢?
左图求的是正方形比圆多的面积,右图求的是圆比正方形多的面积
例3:下图中的两个圆半径都是1m,你能求出正方形和圆之间部分的面积吗?
二、例题讲解
从图(1)可以看出:
正方形的面积:2×2=4(m )
4-3.14=0.86(m )
图(1)
右图中正方形的边长就是圆的直径。
半径是1厘米,直径是2厘米。
圆的面积:3.14×1 =3.14(m )
二、例题讲解
3.14-2=1.14(m )
从图(2)可以看出:
下图中正方形的边长是多少呢?
可以把图中的正方形看成两个三角形,它的底是圆的直径,高是圆的半径。
图(2)
三、例题讲解
左图:(2r) -3.14×r =0.86r
答:左图中正方形与圆之间的面积是0.86 m ,
右图中圆与正方形之间的面积是1.14 m 。
那么我们解答得对不对呢?有什么方法验证吗?
如果两个圆的半径都是r,结果又是怎样的?
右图:3.14×r -( ×2r×r)×2=1.14r
2
1
当r=1 m时,和前面的结果完全一致。
三、新知运用
1.右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24.8 cm。外面的圆与内部的正方形之间的面积是多少?(教材P70做一做)
答:外面的圆与内部的正方形之间的面积约是175.3 cm 。
1.14×(24.8÷2) =175.2864
≈175.3(cm )
三、新知运用
2.土楼是福建、广东等地区的一种建筑形式。被列入“世界物质文化名录”。土楼的外围形状有圆形、方形、椭圆形等,圭峰楼和德逊楼是福建省南靖县两座地面是圆环形的土楼。圭峰楼外直径33米,内直径14米。德逊楼外直径26.4米,内直径14.4米。两座土楼的房屋占地面积相差多少?(教材P73第12题)
答:两座土楼的房屋占地面积相差316.669m 。
3.14×(16.5 -7 )-3.14×(13.2 -7.2 )
圭峰楼外半径:16.5米 内半径:7米
德逊楼外半径:13.2米 内半径:7.2米
=701.005-384.336
=316.669(m )
如何求“外方内圆”和“外圆内方”之间部分的面积?
四、课堂小结
(2r) -3.14×r =0.86r
3.14×r -( ×2r×r)×2=1.14r
2
1
“外方内圆”之间部分的面积是0.86r ;
“外圆内方”之间部分的面积是1.14r 。
五、课后作业
完成课本“练习十七”第71页第7题、第8题。
聪明出于勤奋,天才在于积累。
圆
5
人教版·六年级上册
第6课时 圆环的面积
一、新课引入
1.求出下列图形的面积。
d=6cm
r=2cm
c=12.56
r=d÷2=6÷2=3(cm)
s=πr2
=3.14×32
=28.26(cm2)
s=πr2
=3.14×22
=12.56(cm2)
r=c÷π÷2
=12.56÷3.14÷2
=2(cm)
s=πr2
=3.14×22
=12.56(cm2)
2.画图
一、新课引入
(1)用圆规画一个半径是1cm的圆,并标上圆心0;
(2)圆心相同,再画一个半径是2cm的圆。
0
像这样的图形我们称之为圆环。
二、例题讲解
生活中的圆环。
二、例题讲解
例2:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
怎样利用内圆和外圆的面积求出圆环的面积?
圆环面积=外圆面积–内圆面积
我是这样想的……
二、例题讲解
3.14×6 -3.14×2
=113.04-12.56
=100.48(cm )
3.14×(6 -2 )
=3.14×32
=100.48(cm )
答:圆环的面积是100.48 cm 。
我是这样想的……
还可以这样计算……
例2:光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
二、例题讲解
圆环面积=
πR2
- πr2
外圆面积-内圆面积
S环
=
S环 = π(R2 – r2)
或
如何求圆环的面积?
0
r
R
三、新知运用
50÷2=25(m) 10÷2=5(m)
答:草坪的占地面积是1884m 。
1. 一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?(教材P68做一做第2题)
3.14×(25 -5 )
=3.14×600
=1884(m )
要求草坪的占地面积,也就是求圆环的面积。
2.图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。(教材P72第6题)
三、新知运用
6cm
阴影部分的面积=大圆面积—小圆面积
大圆半径等于小圆的直径
R=6cm
r=6÷2=3cm
S=πR2- πr2
= π(R2 – r2)
=3.14×(62–32)
=84.78(cm )
答:阴影部分的面积84.78cm 。
如何计算圆环的面积?
四、课堂小结
圆环面积=
πR2
- πr2
外圆面积-内圆面积
S环
=
S环 = π(R2 – r2)
或
0
r
R
圆
5
人教版·六年级上册
解决问题
一、新课引入
中国建筑和生活中经常能见到“外方内圆”和“外圆内方”的设计。
例3:下图中的两个圆半径都是1m,你能求出正方形和圆之间部分的面积吗?
二、例题讲解
二、例题讲解
题目中都告诉了我们什么数学信息?
上图中两个圆的半径都是 1 m,怎样求正方形和圆之间部分的面积呢?
左图求的是正方形比圆多的面积,右图求的是圆比正方形多的面积
例3:下图中的两个圆半径都是1m,你能求出正方形和圆之间部分的面积吗?
二、例题讲解
从图(1)可以看出:
正方形的面积:2×2=4(m )
4-3.14=0.86(m )
图(1)
右图中正方形的边长就是圆的直径。
半径是1厘米,直径是2厘米。
圆的面积:3.14×1 =3.14(m )
二、例题讲解
3.14-2=1.14(m )
从图(2)可以看出:
下图中正方形的边长是多少呢?
可以把图中的正方形看成两个三角形,它的底是圆的直径,高是圆的半径。
图(2)
三、例题讲解
左图:(2r) -3.14×r =0.86r
答:左图中正方形与圆之间的面积是0.86 m ,
右图中圆与正方形之间的面积是1.14 m 。
那么我们解答得对不对呢?有什么方法验证吗?
如果两个圆的半径都是r,结果又是怎样的?
右图:3.14×r -( ×2r×r)×2=1.14r
2
1
当r=1 m时,和前面的结果完全一致。
三、新知运用
1.右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24.8 cm。外面的圆与内部的正方形之间的面积是多少?(教材P70做一做)
答:外面的圆与内部的正方形之间的面积约是175.3 cm 。
1.14×(24.8÷2) =175.2864
≈175.3(cm )
三、新知运用
2.土楼是福建、广东等地区的一种建筑形式。被列入“世界物质文化名录”。土楼的外围形状有圆形、方形、椭圆形等,圭峰楼和德逊楼是福建省南靖县两座地面是圆环形的土楼。圭峰楼外直径33米,内直径14米。德逊楼外直径26.4米,内直径14.4米。两座土楼的房屋占地面积相差多少?(教材P73第12题)
答:两座土楼的房屋占地面积相差316.669m 。
3.14×(16.5 -7 )-3.14×(13.2 -7.2 )
圭峰楼外半径:16.5米 内半径:7米
德逊楼外半径:13.2米 内半径:7.2米
=701.005-384.336
=316.669(m )
如何求“外方内圆”和“外圆内方”之间部分的面积?
四、课堂小结
(2r) -3.14×r =0.86r
3.14×r -( ×2r×r)×2=1.14r
2
1
“外方内圆”之间部分的面积是0.86r ;
“外圆内方”之间部分的面积是1.14r 。
五、课后作业
完成课本“练习十七”第71页第7题、第8题。
聪明出于勤奋,天才在于积累。
