人教版数学六年级上册5圆—— 扇形的面积 课件(22张ppt)
文档属性
| 名称 | 人教版数学六年级上册5圆—— 扇形的面积 课件(22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
圆
5
人教版·六年级上册
第9课时 扇形的认识
一、新课引入
扇形窗
扇子
扇贝
扇形藻
这些物体的名称都含有“扇”字,那什么是扇形呢?
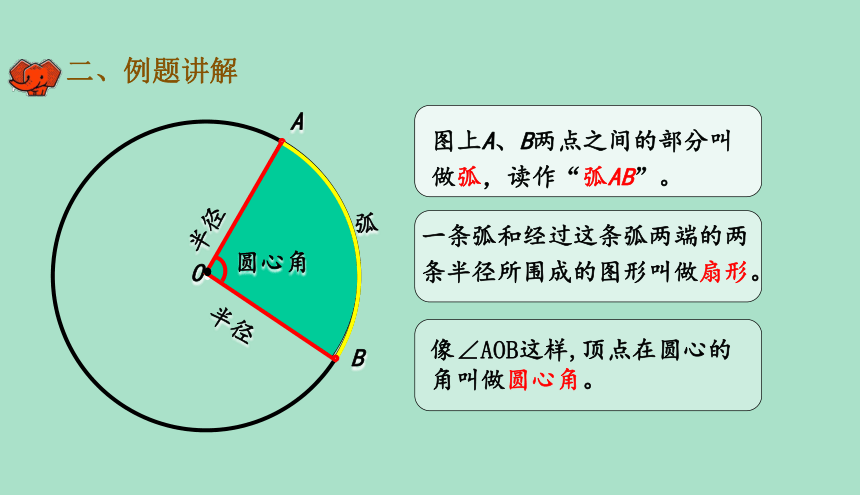
A
B
O
圆心角
半径
半径
弧
图上A、B两点之间的部分叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
像∠AOB这样,顶点在圆心的角叫做圆心角。
二、例题讲解
二、例题讲解
在同一个圆中,扇形的大小与什么有关系呢?
我发现在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
在同一个圆里,圆心角越大,所对应的扇形越大;圆心角越小,所对应的扇形越小。
二、例题讲解
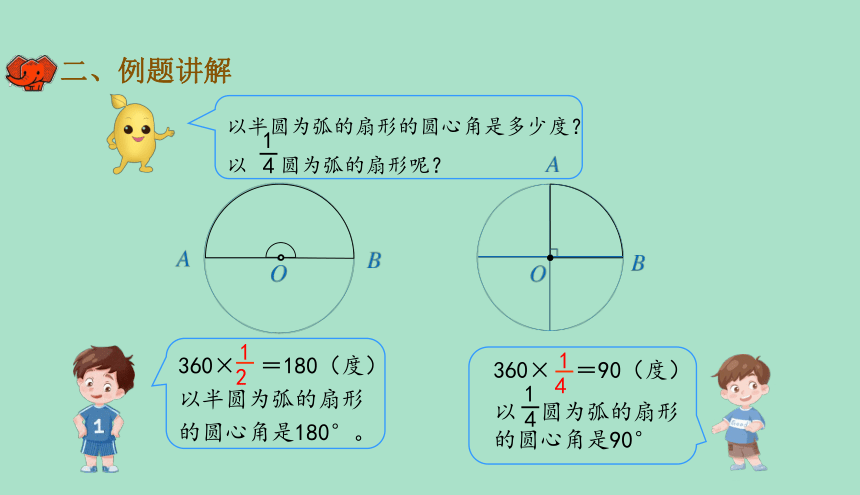
以半圆为弧的扇形的圆心角是多少度?
以 圆为弧的扇形呢?
4
1
360× =180(度)以半圆为弧的扇形的圆心角是180°。
2
1
360× =90(度)
以 圆为弧的扇形的圆心角是90°
4
1
4
1
三、新知运用
A
0
B
A
0
B
A
0
B
A
0
B
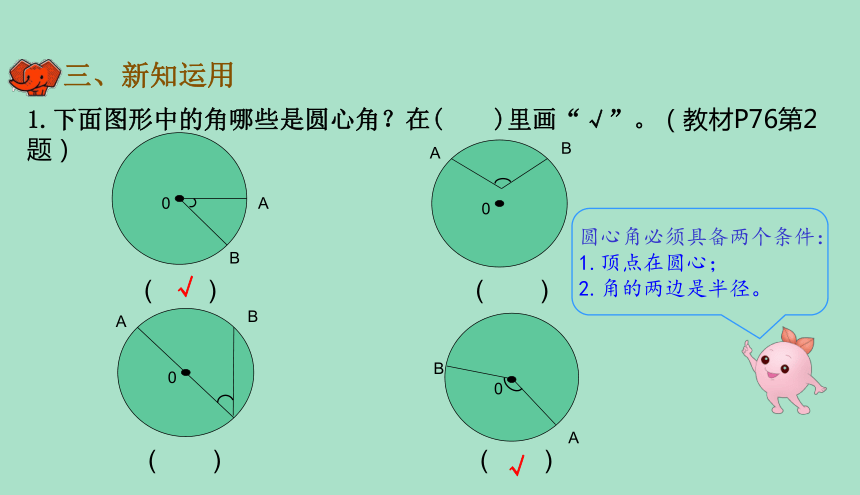
1.下面图形中的角哪些是圆心角?在( )里画“√”。(教材P76第2题)
( )
( )
( )
( )
√
√
圆心角必须具备两个条件:
1.顶点在圆心;
2.角的两边是半径。
三、新知运用
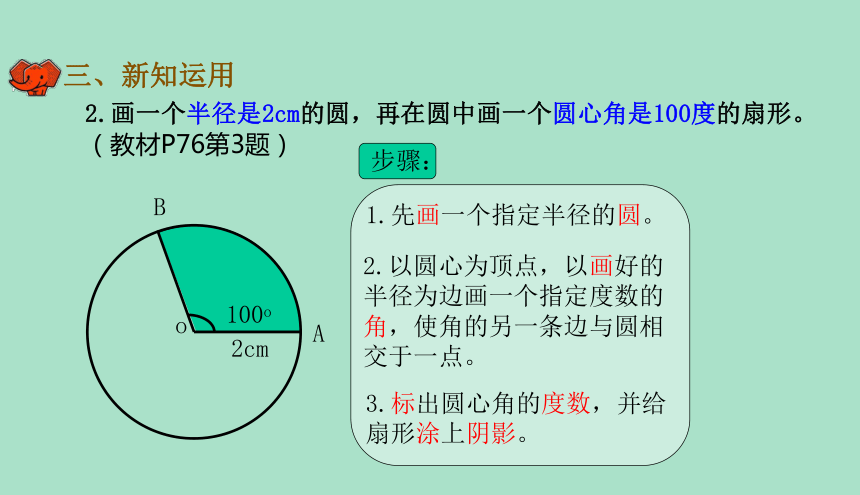
2.画一个半径是2cm的圆,再在圆中画一个圆心角是100度的扇形。(教材P76第3题)
2cm
o
A
B
100o
步骤:
1.先画一个指定半径的圆。
2.以圆心为顶点,以画好的半径为边画一个指定度数的角,使角的另一条边与圆相交于一点。
3.标出圆心角的度数,并给扇形涂上阴影。
三、新知运用
生活中见过这些图案吗?
三、新知运用
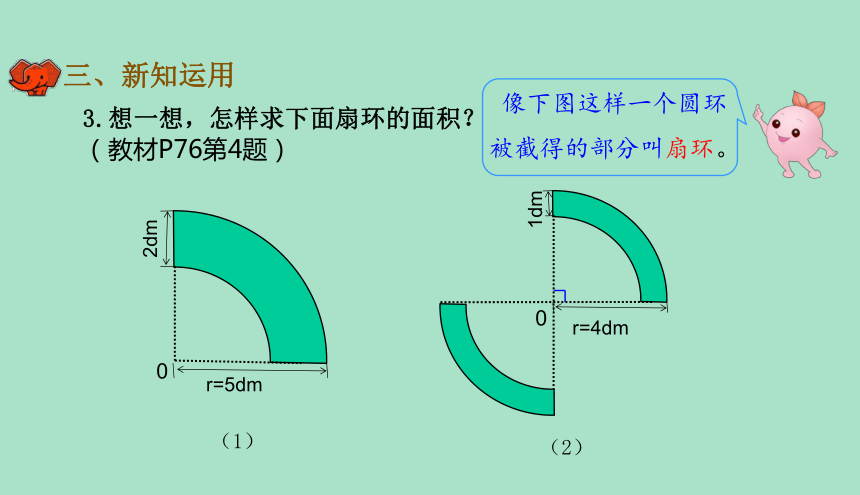
像下图这样一个圆环被截得的部分叫扇环。
(1)
(2)
3.想一想,怎样求下面扇环的面积?(教材P76第4题)
2dm
r=5dm
0
1dm
r=4dm
0
三、新知运用
3.想一想,怎样求下面扇环的面积?(教材P76第4题)
2dm
r=5dm
0
此扇环的面积就相当于是圆环面积的 。
4
1
S= π(R2 – r2)
4
1
= ×3.14×(52–32)
=12.56(dm )
由题可得外圆半径是5dm,内圆半径是3dm。
4
1
三、新知运用
3.想一想,怎样求下面扇环的面积?(教材P76第4题)
1dm
r=4dm
0
此扇环的面积就相当于是圆环面积的 。
2
1
S= π(R2 – r2)
2
1
= ×3.14×(42–32)
=10.99(dm )
由题可得外圆半径是4dm,内圆半径是3dm。
2
1
四、课堂小结
回顾本节课,你学会了什么?
A
B
O
圆心角
半径
半径
弧
在同一个圆里,圆心角越大,所对应的扇形越大;圆心角越小,所对应的扇形越小。
巩固练习
二、课堂练习
1. 你见过“驴拉磨”吗?如果驴绕着一个半径
为1.2 m的圆走一圈,大约要走多少米?
2×3.14×1.2=7.536(m)
答:大约要走7.536米。
求大约要走多少米就是求圆的周长。
圆的周长与面积
知识点1
(教材P78第1题)
二、课堂练习
2. 下图中的双面绣作品中间部分的画是一个直径是20 cm的圆。这幅画的面积是多少?
3.14×(20÷2) =314(cm )
答:这幅画的面积是314 cm 。
先求出半径就可以求出圆的面积。
基础练习
(教材P78第2题)
一、复习巩固
用C表示圆的周长,
则C=( )或C=( )。
πd
πr2
2πr
用S表示圆的面积,
则S=( )
知识总结
二、课堂练习
1. 儿童乐园要修建一个圆形旋转木马场地,木马旋转范围的直径是8 m,周边还要留出1 m宽的小路,并在外侧围上栏杆,这块场地的占地面积是多少?
3.14×(8÷2+1) =78.5(m )
答:这块场地的占地面积是78.5 m 。
占地面积就是指木马旋转的面积以及小路的面积,合起来就是一个大圆的面积。
(教材P78第4题)
二、课堂练习
2. 一个羊圈依墙而建,呈半圆形,半径是5 m。
(1)修这个羊圈需要多长的栅栏?
2×3.14×5÷2=15.7(m)
答:修这个羊圈需要15.7 m的栅栏。
(2)如果要扩建这个羊圈,把它的直径增加2 m。羊圈的面积增加了多少?
3.14×[(5+2÷2) -5 ]÷2=17.27(m )
答:羊圈的面积增加了17.27 m 。
5m
1m
(教材P78第5题)
二、课堂练习
3.如下图,一台压路机的前轮直径是1.7 m, 如果前轮每分钟转动6周,压路机10分钟前进多远?
3.14×1.7×6×10=320.28(m)
答:压路机10分钟前进320.28 m。
先求一个轮子的周长,一分钟就是6个圆的周长。
(教材P79第7题)
二、课堂练习
4. 如图,学校操场的跑道由正方形的两条对边和两个半圆组成。小晨在操场上跑了5圈,一共是多少米?
(3.14×50+50×2)×5=1285(m)
答:一共是1285 m 。
50 m
操场跑道的长度等于一个整圆的周长与两条直的跑道的长度之和。
(教材P79第10题)
1. 如下图,中间是边长为1 cm的正方形,与这个正方形每一条边相连的都是圆心角为90°的扇形,整个图形的面积是多少?
1 +3.14×1 =4.14(cm )
答:整个图形的面积是4.14 cm 。
整个图形的面积相当于一个正方形和一个圆的面积。
三、拓展提升
(教材P79第9题)
五、课后作业
完成课本“练习十六”第76页第1题及练习册中对应课时练习。
圆
5
人教版·六年级上册
第9课时 扇形的认识
一、新课引入
扇形窗
扇子
扇贝
扇形藻
这些物体的名称都含有“扇”字,那什么是扇形呢?
A
B
O
圆心角
半径
半径
弧
图上A、B两点之间的部分叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
像∠AOB这样,顶点在圆心的角叫做圆心角。
二、例题讲解
二、例题讲解
在同一个圆中,扇形的大小与什么有关系呢?
我发现在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
在同一个圆里,圆心角越大,所对应的扇形越大;圆心角越小,所对应的扇形越小。
二、例题讲解
以半圆为弧的扇形的圆心角是多少度?
以 圆为弧的扇形呢?
4
1
360× =180(度)以半圆为弧的扇形的圆心角是180°。
2
1
360× =90(度)
以 圆为弧的扇形的圆心角是90°
4
1
4
1
三、新知运用
A
0
B
A
0
B
A
0
B
A
0
B
1.下面图形中的角哪些是圆心角?在( )里画“√”。(教材P76第2题)
( )
( )
( )
( )
√
√
圆心角必须具备两个条件:
1.顶点在圆心;
2.角的两边是半径。
三、新知运用
2.画一个半径是2cm的圆,再在圆中画一个圆心角是100度的扇形。(教材P76第3题)
2cm
o
A
B
100o
步骤:
1.先画一个指定半径的圆。
2.以圆心为顶点,以画好的半径为边画一个指定度数的角,使角的另一条边与圆相交于一点。
3.标出圆心角的度数,并给扇形涂上阴影。
三、新知运用
生活中见过这些图案吗?
三、新知运用
像下图这样一个圆环被截得的部分叫扇环。
(1)
(2)
3.想一想,怎样求下面扇环的面积?(教材P76第4题)
2dm
r=5dm
0
1dm
r=4dm
0
三、新知运用
3.想一想,怎样求下面扇环的面积?(教材P76第4题)
2dm
r=5dm
0
此扇环的面积就相当于是圆环面积的 。
4
1
S= π(R2 – r2)
4
1
= ×3.14×(52–32)
=12.56(dm )
由题可得外圆半径是5dm,内圆半径是3dm。
4
1
三、新知运用
3.想一想,怎样求下面扇环的面积?(教材P76第4题)
1dm
r=4dm
0
此扇环的面积就相当于是圆环面积的 。
2
1
S= π(R2 – r2)
2
1
= ×3.14×(42–32)
=10.99(dm )
由题可得外圆半径是4dm,内圆半径是3dm。
2
1
四、课堂小结
回顾本节课,你学会了什么?
A
B
O
圆心角
半径
半径
弧
在同一个圆里,圆心角越大,所对应的扇形越大;圆心角越小,所对应的扇形越小。
巩固练习
二、课堂练习
1. 你见过“驴拉磨”吗?如果驴绕着一个半径
为1.2 m的圆走一圈,大约要走多少米?
2×3.14×1.2=7.536(m)
答:大约要走7.536米。
求大约要走多少米就是求圆的周长。
圆的周长与面积
知识点1
(教材P78第1题)
二、课堂练习
2. 下图中的双面绣作品中间部分的画是一个直径是20 cm的圆。这幅画的面积是多少?
3.14×(20÷2) =314(cm )
答:这幅画的面积是314 cm 。
先求出半径就可以求出圆的面积。
基础练习
(教材P78第2题)
一、复习巩固
用C表示圆的周长,
则C=( )或C=( )。
πd
πr2
2πr
用S表示圆的面积,
则S=( )
知识总结
二、课堂练习
1. 儿童乐园要修建一个圆形旋转木马场地,木马旋转范围的直径是8 m,周边还要留出1 m宽的小路,并在外侧围上栏杆,这块场地的占地面积是多少?
3.14×(8÷2+1) =78.5(m )
答:这块场地的占地面积是78.5 m 。
占地面积就是指木马旋转的面积以及小路的面积,合起来就是一个大圆的面积。
(教材P78第4题)
二、课堂练习
2. 一个羊圈依墙而建,呈半圆形,半径是5 m。
(1)修这个羊圈需要多长的栅栏?
2×3.14×5÷2=15.7(m)
答:修这个羊圈需要15.7 m的栅栏。
(2)如果要扩建这个羊圈,把它的直径增加2 m。羊圈的面积增加了多少?
3.14×[(5+2÷2) -5 ]÷2=17.27(m )
答:羊圈的面积增加了17.27 m 。
5m
1m
(教材P78第5题)
二、课堂练习
3.如下图,一台压路机的前轮直径是1.7 m, 如果前轮每分钟转动6周,压路机10分钟前进多远?
3.14×1.7×6×10=320.28(m)
答:压路机10分钟前进320.28 m。
先求一个轮子的周长,一分钟就是6个圆的周长。
(教材P79第7题)
二、课堂练习
4. 如图,学校操场的跑道由正方形的两条对边和两个半圆组成。小晨在操场上跑了5圈,一共是多少米?
(3.14×50+50×2)×5=1285(m)
答:一共是1285 m 。
50 m
操场跑道的长度等于一个整圆的周长与两条直的跑道的长度之和。
(教材P79第10题)
1. 如下图,中间是边长为1 cm的正方形,与这个正方形每一条边相连的都是圆心角为90°的扇形,整个图形的面积是多少?
1 +3.14×1 =4.14(cm )
答:整个图形的面积是4.14 cm 。
整个图形的面积相当于一个正方形和一个圆的面积。
三、拓展提升
(教材P79第9题)
五、课后作业
完成课本“练习十六”第76页第1题及练习册中对应课时练习。
