人教A版(2019)高中数学选择性必修第一册 2.5.2 圆与圆的位置关系(28张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 2.5.2 圆与圆的位置关系(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 18:07:24 | ||
图片预览







文档简介
2.5.2 圆与圆的位置关系
激趣诱思
知识点拨
“打水漂”游戏别名轻功水上漂、七点漂、漂瓦,是用扁形瓦片或石片,在手上呈水平放置后,用力飞出,石片擦水面飞行,石片碰水面后弹起再飞,石片不断在水面上向前弹跳,直至沉水.在这一过程中,石片与水面接触形成了一个个逐渐扩大的圆,这些圆在变化的过程中位置关系是怎样的?
激趣诱思
知识点拨
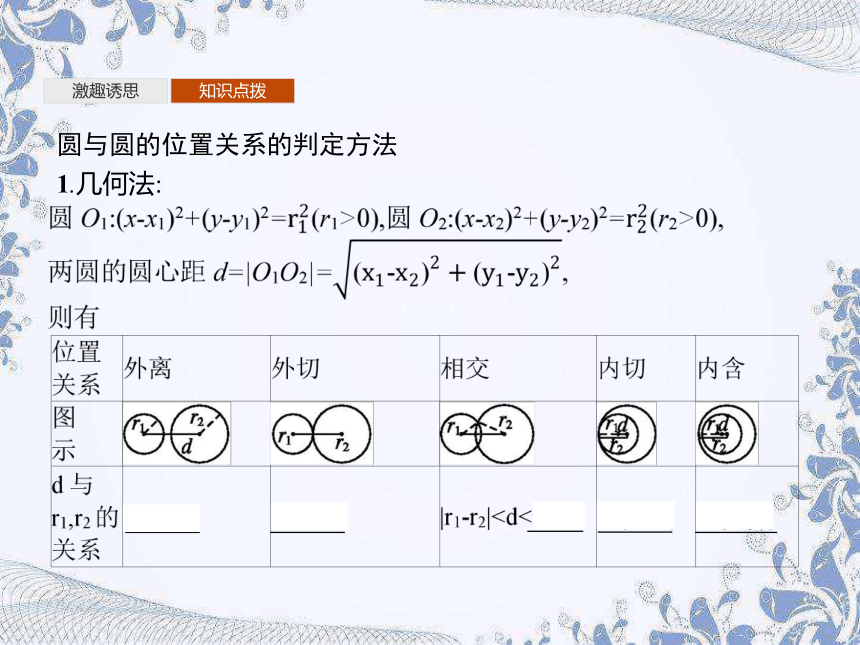
圆与圆的位置关系的判定方法
1.几何法:
激趣诱思
知识点拨
激趣诱思
知识点拨
微练习
(1)判断下列两圆的位置关系:
①(x+2)2+(y-2)2=1与(x-2)2+(y-5)2=16.
②x2+y2+6x-7=0与x2+y2+6y-27=0.
解:①根据题意得,两圆的半径分别为r1=1和r2=4,两圆的圆心距
因为d=r1+r2,所以两圆外切.
②将两圆的方程化为标准方程,得(x+3)2+y2=16,x2+(y+3)2=36,
故两圆的半径分别为r1=4和r2=6.
两圆的圆心距
激趣诱思
知识点拨
(2)两圆x2+y2=1和(x+4)2+(y-a)2=25相切,则实数a的值为 .?
探究一
探究二
探究三
素养形成
当堂检测
判断两圆的位置关系
例1已知圆C1:x2+y2-2ax-2y+a2-15=0(a>0),圆C2:x2+y2-4ax-2y+4a2=0(a>0).试求a为何值时,两圆C1,C2的位置关系为:
(1)相切;(2)相交;(3)外离;(4)内含?
思路分析:求出圆心距,与两半径的和或差比较求出a的值.
探究一
探究二
探究三
素养形成
当堂检测
解:圆C1,C2的方程,经配方后可得
C1:(x-a)2+(y-1)2=16,
C2:(x-2a)2+(y-1)2=1,
∴圆心C1(a,1),C2(2a,1),半径r1=4,r2=1.
(1)当|C1C2|=r1+r2=5,即a=5时,两圆外切;
当|C1C2|=r1-r2=3,即a=3时,两圆内切.
(2)当3<|C1C2|<5,即3 (3)当|C1C2|>5,即a>5时,两圆外离.
(4)当|C1C2|<3,即0探究一
探究二
探究三
素养形成
当堂检测
反思感悟判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系;
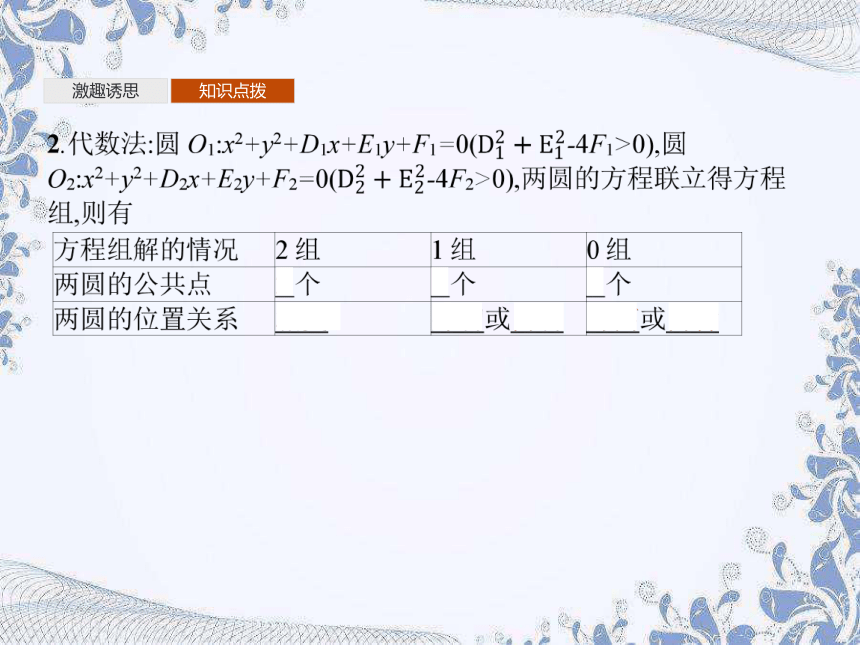
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解的组数问题.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究若两圆x2+y2=a与x2+y2+6x-8y-11=0内切,则a的值为 .?
答案:121或1
探究一
探究二
探究三
素养形成
当堂检测
两圆相交问题
例2已知圆C1:x2+y2+6x-4=0和圆C2:x2+y2+6y-28=0.
(1)求两圆公共弦所在直线的方程及弦长;
(2)求经过两圆交点且圆心在直线x-y-4=0上的圆的方程.
思路分析:(1)两圆方程相减求出公共弦所在直线方程,再根据半径、弦心距、弦长的关系求出弦长.
(2)可求出两圆的交点坐标,结合圆心在直线x-y-4=0上求出圆心坐标与半径,也可利用圆系方程求解.
探究一
探究二
探究三
素养形成
当堂检测
①-②,得x-y+4=0.
∵A,B两点坐标都满足此方程,
∴x-y+4=0即为两圆公共弦所在直线的方程.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟相交弦及圆系方程问题的解决
1.求两圆的公共弦所在直线的方程的方法:将两圆方程相减即得两圆公共弦所在直线方程,但必须注意只有当两圆方程中二次项系数相同时,才能如此求解,否则应先调整系数.
2.求两圆公共弦长的方法:一是联立两圆方程求出交点坐标,再用距离公式求解;二是先求出两圆公共弦所在的直线方程,再利用半径长、弦心距和弦长的一半构成的直角三角形求解.
3.已知圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则过两圆交点的圆的方程可设为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1).
探究一
探究二
探究三
素养形成
当堂检测
变式训练两圆相交于两点A(1,3)和B(m,-1),两圆圆心都在直线
x-y+c=0上,则m+c的值为 .?
∴AB的中点坐标为(3,1).
AB的中点在直线x-y+c=0上,
∴3-1+c=0,∴c=-2,
∴m+c=5-2=3.
答案:3
探究一
探究二
探究三
素养形成
当堂检测
两圆相切问题
思路分析:设圆的方程,利用两圆外切和直线与圆相切建立方程组求得.
解:设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
由题知所求圆与圆x2+y2-2x=0外切,
探究一
探究二
探究三
素养形成
当堂检测
延伸探究1将本例变为“求与圆x2+y2-2x=0外切,圆心在x轴上,且过点(3,- )的圆的方程”,如何求?
解:因为圆心在x轴上,
所以可设圆心坐标为(a,0),设半径为r,
则所求圆的方程为(x-a)2+y2=r2,
探究一
探究二
探究三
素养形成
当堂检测
延伸探究2将本例改为“若圆x2+y2-2x=0与圆x2+y2-8x-8y+m=0相外切”,试求实数m的值.
反思感悟处理两圆相切问题的两个步骤
(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须考虑分两圆内切还是外切两种情况讨论.
(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值(内切时)或两圆半径之和(外切时).
探究一
探究二
探究三
素养形成
当堂检测
圆系方程
经过两个圆的公共点可作无数个圆,这无数个圆可组成一个圆系.与已知圆有相同圆心的圆也可以组成一个圆系,等等.常见圆系方程有如下几种:
1.过直线与圆的交点的圆系:过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0;特别地,当直线与圆相切于点P时,上述方程表示与直线和圆都相切于点P的圆.
2.过两个圆的交点的圆系:过两圆x2+y2+D1x+E1y+F1=0,x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1),此圆系不含圆x2+y2+D2x+E2y+F2=0.
探究一
探究二
探究三
素养形成
当堂检测
3.同心圆系:与圆x2+y2+Dx+Ey+F=0同心的圆系方程为x2+y2+Dx+Ey+λ=0;或表示为与已知圆(x-a)2+(y-b)2=r2同心的圆系方程为(x-a)2+(y-b)2=R2(其中a,b为定值).
对圆系方程可作以下推广:对过两已知圆交点的圆系方程,当λ=-1时,得到(D1-D2)x+(E1-E2)y+F1-F2=0,此为两圆公共弦所在直线方程.因此,如果两圆相交,两圆的方程相减就得到两圆公共弦所在直线的方程.由此可推广:经过两曲线f(x,y)=0,g(x,y)=0交点的曲线系方程为f(x,y)+λg(x,y)=0
探究一
探究二
探究三
素养形成
当堂检测
典例1一圆过圆x2+y2-2x=0和直线x+2y-3=0的交点,且圆心在y轴上,则这个圆的方程是( )
A.x2+y2-4x-4y+6=0
B.x2+y2+4y-6=0
C.x2+y2-2x=0
D.x2+y2+4x-6=0
答案:B
探究一
探究二
探究三
素养形成
当堂检测
典例2已知两个圆C1:x2+y2=4,C2:x2+y2-2x-4y+4=0,直线l:x+2y=0,求经过C1和C2的交点且和l相切的圆的方程.
探究一
探究二
探究三
素养形成
当堂检测
点评圆与直线相切的问题可利用圆心到切线的距离等于半径列等式.求经过两圆交点的圆可考虑圆系,但要考虑λ≠-1,另外由于圆系中不包括圆x2+y2=4,因此应检验圆x2+y2=4是否也满足条件.
探究一
探究二
探究三
素养形成
当堂检测
1.两圆x2+y2-1=0和x2+y2-4x+2y-4=0的位置关系是( )
A.内切 B.相交
C.外切 D.外离
解析:圆x2+y2-1=0表示以O1(0,0)点为圆心,以R1=1为半径的圆.
圆x2+y2-4x+2y-4=0表示以O2(2,-1)点为圆心,以R2=3为半径的圆.
∵|O1O2|= ,
∴R2-R1<|O1O2| ∴圆x2+y2-1=0和圆x2+y2-4x+2y-4=0相交.
答案:B
探究一
探究二
探究三
素养形成
当堂检测
2.圆C1:x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦所在的直线方程是 .?
解析:两圆的方程相减得公共弦所在的直线方程为4x+3y-2=0.
答案:4x+3y-2=0
探究一
探究二
探究三
素养形成
当堂检测
3.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程为( )
A.(x-4)2+(y-6)2=16
B.(x±4)2+(y-6)2=16
C.(x-4)2+(y-6)2=36
D.(x±4)2+(y-6)2=36
解析:设所求圆心坐标为(a,b),则|b|=6.
由题意,得a2+(b-3)2=(6-1)2=25.
若b=6,则a=±4;若b=-6,则a无解.
故所求圆方程为(x±4)2+(y-6)2=36.
答案:D
探究一
探究二
探究三
素养形成
当堂检测
4.若圆C1:x2+y2=4与圆C2:x2+y2-2ax+a2-1=0内切,则a等于 .?
解析:圆C1的圆心C1(0,0),半径r1=2.
圆C2可化为(x-a)2+y2=1,即圆心C2(a,0),半径r2=1,若两圆内切,需
答案:±1
激趣诱思
知识点拨
“打水漂”游戏别名轻功水上漂、七点漂、漂瓦,是用扁形瓦片或石片,在手上呈水平放置后,用力飞出,石片擦水面飞行,石片碰水面后弹起再飞,石片不断在水面上向前弹跳,直至沉水.在这一过程中,石片与水面接触形成了一个个逐渐扩大的圆,这些圆在变化的过程中位置关系是怎样的?
激趣诱思
知识点拨
圆与圆的位置关系的判定方法
1.几何法:
激趣诱思
知识点拨
激趣诱思
知识点拨
微练习
(1)判断下列两圆的位置关系:
①(x+2)2+(y-2)2=1与(x-2)2+(y-5)2=16.
②x2+y2+6x-7=0与x2+y2+6y-27=0.
解:①根据题意得,两圆的半径分别为r1=1和r2=4,两圆的圆心距
因为d=r1+r2,所以两圆外切.
②将两圆的方程化为标准方程,得(x+3)2+y2=16,x2+(y+3)2=36,
故两圆的半径分别为r1=4和r2=6.
两圆的圆心距
激趣诱思
知识点拨
(2)两圆x2+y2=1和(x+4)2+(y-a)2=25相切,则实数a的值为 .?
探究一
探究二
探究三
素养形成
当堂检测
判断两圆的位置关系
例1已知圆C1:x2+y2-2ax-2y+a2-15=0(a>0),圆C2:x2+y2-4ax-2y+4a2=0(a>0).试求a为何值时,两圆C1,C2的位置关系为:
(1)相切;(2)相交;(3)外离;(4)内含?
思路分析:求出圆心距,与两半径的和或差比较求出a的值.
探究一
探究二
探究三
素养形成
当堂检测
解:圆C1,C2的方程,经配方后可得
C1:(x-a)2+(y-1)2=16,
C2:(x-2a)2+(y-1)2=1,
∴圆心C1(a,1),C2(2a,1),半径r1=4,r2=1.
(1)当|C1C2|=r1+r2=5,即a=5时,两圆外切;
当|C1C2|=r1-r2=3,即a=3时,两圆内切.
(2)当3<|C1C2|<5,即3
(4)当|C1C2|<3,即0
探究二
探究三
素养形成
当堂检测
反思感悟判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系;
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解的组数问题.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究若两圆x2+y2=a与x2+y2+6x-8y-11=0内切,则a的值为 .?
答案:121或1
探究一
探究二
探究三
素养形成
当堂检测
两圆相交问题
例2已知圆C1:x2+y2+6x-4=0和圆C2:x2+y2+6y-28=0.
(1)求两圆公共弦所在直线的方程及弦长;
(2)求经过两圆交点且圆心在直线x-y-4=0上的圆的方程.
思路分析:(1)两圆方程相减求出公共弦所在直线方程,再根据半径、弦心距、弦长的关系求出弦长.
(2)可求出两圆的交点坐标,结合圆心在直线x-y-4=0上求出圆心坐标与半径,也可利用圆系方程求解.
探究一
探究二
探究三
素养形成
当堂检测
①-②,得x-y+4=0.
∵A,B两点坐标都满足此方程,
∴x-y+4=0即为两圆公共弦所在直线的方程.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟相交弦及圆系方程问题的解决
1.求两圆的公共弦所在直线的方程的方法:将两圆方程相减即得两圆公共弦所在直线方程,但必须注意只有当两圆方程中二次项系数相同时,才能如此求解,否则应先调整系数.
2.求两圆公共弦长的方法:一是联立两圆方程求出交点坐标,再用距离公式求解;二是先求出两圆公共弦所在的直线方程,再利用半径长、弦心距和弦长的一半构成的直角三角形求解.
3.已知圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则过两圆交点的圆的方程可设为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1).
探究一
探究二
探究三
素养形成
当堂检测
变式训练两圆相交于两点A(1,3)和B(m,-1),两圆圆心都在直线
x-y+c=0上,则m+c的值为 .?
∴AB的中点坐标为(3,1).
AB的中点在直线x-y+c=0上,
∴3-1+c=0,∴c=-2,
∴m+c=5-2=3.
答案:3
探究一
探究二
探究三
素养形成
当堂检测
两圆相切问题
思路分析:设圆的方程,利用两圆外切和直线与圆相切建立方程组求得.
解:设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
由题知所求圆与圆x2+y2-2x=0外切,
探究一
探究二
探究三
素养形成
当堂检测
延伸探究1将本例变为“求与圆x2+y2-2x=0外切,圆心在x轴上,且过点(3,- )的圆的方程”,如何求?
解:因为圆心在x轴上,
所以可设圆心坐标为(a,0),设半径为r,
则所求圆的方程为(x-a)2+y2=r2,
探究一
探究二
探究三
素养形成
当堂检测
延伸探究2将本例改为“若圆x2+y2-2x=0与圆x2+y2-8x-8y+m=0相外切”,试求实数m的值.
反思感悟处理两圆相切问题的两个步骤
(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须考虑分两圆内切还是外切两种情况讨论.
(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值(内切时)或两圆半径之和(外切时).
探究一
探究二
探究三
素养形成
当堂检测
圆系方程
经过两个圆的公共点可作无数个圆,这无数个圆可组成一个圆系.与已知圆有相同圆心的圆也可以组成一个圆系,等等.常见圆系方程有如下几种:
1.过直线与圆的交点的圆系:过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0;特别地,当直线与圆相切于点P时,上述方程表示与直线和圆都相切于点P的圆.
2.过两个圆的交点的圆系:过两圆x2+y2+D1x+E1y+F1=0,x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1),此圆系不含圆x2+y2+D2x+E2y+F2=0.
探究一
探究二
探究三
素养形成
当堂检测
3.同心圆系:与圆x2+y2+Dx+Ey+F=0同心的圆系方程为x2+y2+Dx+Ey+λ=0;或表示为与已知圆(x-a)2+(y-b)2=r2同心的圆系方程为(x-a)2+(y-b)2=R2(其中a,b为定值).
对圆系方程可作以下推广:对过两已知圆交点的圆系方程,当λ=-1时,得到(D1-D2)x+(E1-E2)y+F1-F2=0,此为两圆公共弦所在直线方程.因此,如果两圆相交,两圆的方程相减就得到两圆公共弦所在直线的方程.由此可推广:经过两曲线f(x,y)=0,g(x,y)=0交点的曲线系方程为f(x,y)+λg(x,y)=0
探究一
探究二
探究三
素养形成
当堂检测
典例1一圆过圆x2+y2-2x=0和直线x+2y-3=0的交点,且圆心在y轴上,则这个圆的方程是( )
A.x2+y2-4x-4y+6=0
B.x2+y2+4y-6=0
C.x2+y2-2x=0
D.x2+y2+4x-6=0
答案:B
探究一
探究二
探究三
素养形成
当堂检测
典例2已知两个圆C1:x2+y2=4,C2:x2+y2-2x-4y+4=0,直线l:x+2y=0,求经过C1和C2的交点且和l相切的圆的方程.
探究一
探究二
探究三
素养形成
当堂检测
点评圆与直线相切的问题可利用圆心到切线的距离等于半径列等式.求经过两圆交点的圆可考虑圆系,但要考虑λ≠-1,另外由于圆系中不包括圆x2+y2=4,因此应检验圆x2+y2=4是否也满足条件.
探究一
探究二
探究三
素养形成
当堂检测
1.两圆x2+y2-1=0和x2+y2-4x+2y-4=0的位置关系是( )
A.内切 B.相交
C.外切 D.外离
解析:圆x2+y2-1=0表示以O1(0,0)点为圆心,以R1=1为半径的圆.
圆x2+y2-4x+2y-4=0表示以O2(2,-1)点为圆心,以R2=3为半径的圆.
∵|O1O2|= ,
∴R2-R1<|O1O2|
答案:B
探究一
探究二
探究三
素养形成
当堂检测
2.圆C1:x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦所在的直线方程是 .?
解析:两圆的方程相减得公共弦所在的直线方程为4x+3y-2=0.
答案:4x+3y-2=0
探究一
探究二
探究三
素养形成
当堂检测
3.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程为( )
A.(x-4)2+(y-6)2=16
B.(x±4)2+(y-6)2=16
C.(x-4)2+(y-6)2=36
D.(x±4)2+(y-6)2=36
解析:设所求圆心坐标为(a,b),则|b|=6.
由题意,得a2+(b-3)2=(6-1)2=25.
若b=6,则a=±4;若b=-6,则a无解.
故所求圆方程为(x±4)2+(y-6)2=36.
答案:D
探究一
探究二
探究三
素养形成
当堂检测
4.若圆C1:x2+y2=4与圆C2:x2+y2-2ax+a2-1=0内切,则a等于 .?
解析:圆C1的圆心C1(0,0),半径r1=2.
圆C2可化为(x-a)2+y2=1,即圆心C2(a,0),半径r2=1,若两圆内切,需
答案:±1
