人教A版(2019)高中数学选择性必修第一册 3.1.2 椭圆的简单几何性质(34张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 3.1.2 椭圆的简单几何性质(34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览










文档简介
3.1.2 椭圆的简单几何性质
激趣诱思
知识点拨
地球围绕太阳公转的轨道是一个椭圆,太阳处在这个椭圆的一个焦点上.在椭圆轨道上有一个近日点和一个远日点,在近日点时距离太阳14 710万千米,在远日点时距离太阳15 210万千米.事实上,很多天体或飞行器的运行轨道都是椭圆.如神舟九号飞船,于2012年6月16日搭载3名航天员发射升空,之后进入近地点高度200千米,远地点高度329.8千米的椭圆形轨道,然后进行了5次变轨,两天后与天宫一号自动交会对接成功,这是中国首次实现载人空间交会对接任务.
激趣诱思
知识点拨
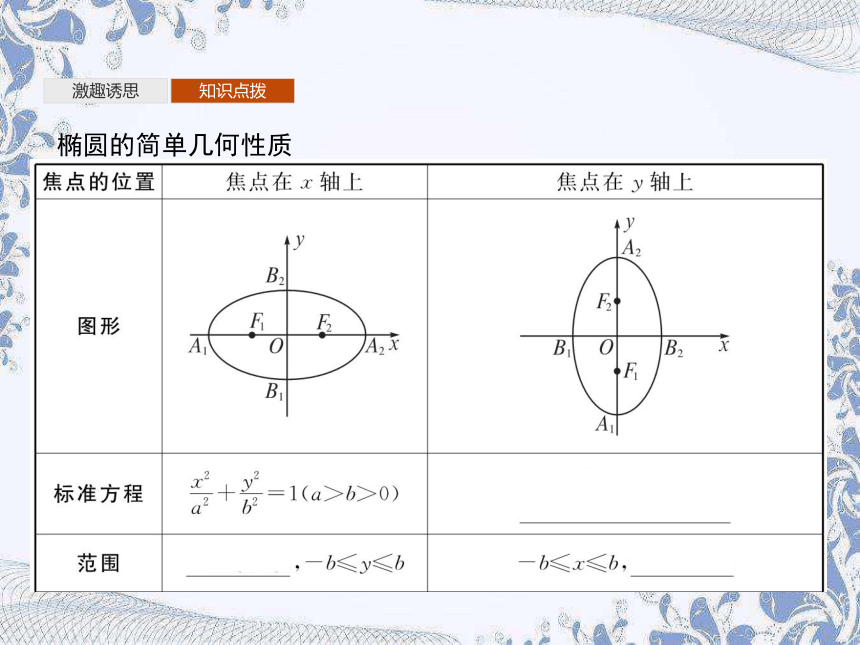
椭圆的简单几何性质
激趣诱思
知识点拨
激趣诱思
知识点拨
名师点拨1.椭圆的范围给出了椭圆上的点的横坐标、纵坐标的取值范围,在求解一些存在性、判断性问题中有着重要的应用,也可用于求最值、求轨迹等问题时的检验等.
2.利用方程研究曲线对称性的方法如下:
(1)若把曲线方程中的x换成-x,方程不变,则曲线关于y轴对称;
(2)若把曲线方程中的y换成-y,方程不变,则曲线关于x轴对称;
(3)若同时把曲线方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.
激趣诱思
知识点拨
微练习
(1)已知椭圆 =1,则其顶点坐标分别为 ,焦点坐标为 ,长轴长等于 ,短轴长等于 ,焦距等于 .若点P(m,n)为该椭圆上任意一点,则m的取值范围是 .?
激趣诱思
知识点拨
(2)椭圆x2+4y2=1的离心率等于( )
答案:A
探究一
探究二
探究三
素养形成
当堂检测
根据椭圆的标准方程研究其几何性质
例1求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究本例中若把椭圆方程改为“9x2+16y2=1”,求其长轴长、短轴长、离心率、焦点和顶点坐标.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟确定椭圆几何性质的基本步骤
(1)化标准,把椭圆方程化成标准形式;
(2)定位置,根据标准方程中x2,y2对应分母的大小来确定焦点位置;
(3)求参数,写出a,b的值,并求出c的值;
(4)写性质,按要求写出椭圆的简单几何性质.
探究一
探究二
探究三
素养形成
当堂检测
长、短轴长分别相等,且椭圆C2的焦点在y轴上.
(1)求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
(2)写出椭圆C2的方程,并研究其性质.
探究一
探究二
探究三
素养形成
当堂检测
根据椭圆的几何性质求其标准方程
例2根据下列条件求椭圆的标准方程:
(2)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为8.
思路分析:(1)焦点位置不确定,应分类讨论;(2)结合图形求出a,b,c的值代入.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),
且|OF|=c,|A1A2|=2b,
∴c=b=4,∴a2=b2+c2=32.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟根据椭圆的性质求方程
1.已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
2.在求椭圆方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2已知椭圆的长轴长是短轴长的2倍,且经过点A(2,0),求椭圆的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
求椭圆的离心率的值(或范围)
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
(方法2)设A(0,b),B(a,0),F(-c,0),
设△FAB的外接圆的方程为x2+y2+Dx+Ey+F=0.
将A,B,F三点的坐标分别代入外接圆方程,
探究一
探究二
探究三
素养形成
当堂检测
答案:(1)A (2)A
探究一
探究二
探究三
素养形成
当堂检测
反思感悟求椭圆离心率及取值范围的两种方法
(2)方程法:若a,c的值不可求,则可根据条件建立a,b,c的关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程或不等式,再将方程或不等式两边同除以a的最高次幂,得到关于e的方程或不等式,即可求得e的值或范围.求离心率的范围时,应根据题意建立a,c的不等式,结合e∈(0,1)确定离心率的范围.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3(1)已知椭圆的焦距不小于短轴长,求椭圆的离心率的取值范围.
探究一
探究二
探究三
素养形成
当堂检测
(2)如图所示,设直线y=2x与椭圆的一个交点为P,
则点P横坐标为c,连接PF1,PF2,则|PF1|=2c.
因为△PF1F2为直角三角形,|F1F2|=2c,
探究一
探究二
探究三
素养形成
当堂检测
反思感悟离心率的求法
(3)若已知a,b,c的关系,则可转化为a,c的方程或不等式,进而得到关于e的方程或不等式进行求解.
探究一
探究二
探究三
素养形成
当堂检测
一题多变——求椭圆的离心率
答案:D
探究一
探究二
探究三
素养形成
当堂检测
变式训练1(变条件)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“∠PF2F1=75°,∠PF1F2=45°”,求椭圆C的离心率.
解:在△PF1F2中,
∵∠PF1F2=45°,∠PF2F1=75°,
∴∠F1PF2=60°,
设|PF1|=m,|PF2|=n,|F1F2|=2c,椭圆的长轴长为2a,
探究一
探究二
探究三
素养形成
当堂检测
变式训练2(变条件,变设问)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“椭圆C上存在点P,使∠F1PF2为钝角”,求椭圆C的离心率的取值范围.
探究一
探究二
探究三
素养形成
当堂检测
1.椭圆6x2+y2=6的长轴的端点坐标是( )
A.(-1,0),(1,0) B.(0,-1),(0,1)
答案:D
探究一
探究二
探究三
素养形成
当堂检测
答案:A
探究一
探究二
探究三
素养形成
当堂检测
答案:A
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
激趣诱思
知识点拨
地球围绕太阳公转的轨道是一个椭圆,太阳处在这个椭圆的一个焦点上.在椭圆轨道上有一个近日点和一个远日点,在近日点时距离太阳14 710万千米,在远日点时距离太阳15 210万千米.事实上,很多天体或飞行器的运行轨道都是椭圆.如神舟九号飞船,于2012年6月16日搭载3名航天员发射升空,之后进入近地点高度200千米,远地点高度329.8千米的椭圆形轨道,然后进行了5次变轨,两天后与天宫一号自动交会对接成功,这是中国首次实现载人空间交会对接任务.
激趣诱思
知识点拨
椭圆的简单几何性质
激趣诱思
知识点拨
激趣诱思
知识点拨
名师点拨1.椭圆的范围给出了椭圆上的点的横坐标、纵坐标的取值范围,在求解一些存在性、判断性问题中有着重要的应用,也可用于求最值、求轨迹等问题时的检验等.
2.利用方程研究曲线对称性的方法如下:
(1)若把曲线方程中的x换成-x,方程不变,则曲线关于y轴对称;
(2)若把曲线方程中的y换成-y,方程不变,则曲线关于x轴对称;
(3)若同时把曲线方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.
激趣诱思
知识点拨
微练习
(1)已知椭圆 =1,则其顶点坐标分别为 ,焦点坐标为 ,长轴长等于 ,短轴长等于 ,焦距等于 .若点P(m,n)为该椭圆上任意一点,则m的取值范围是 .?
激趣诱思
知识点拨
(2)椭圆x2+4y2=1的离心率等于( )
答案:A
探究一
探究二
探究三
素养形成
当堂检测
根据椭圆的标准方程研究其几何性质
例1求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究本例中若把椭圆方程改为“9x2+16y2=1”,求其长轴长、短轴长、离心率、焦点和顶点坐标.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟确定椭圆几何性质的基本步骤
(1)化标准,把椭圆方程化成标准形式;
(2)定位置,根据标准方程中x2,y2对应分母的大小来确定焦点位置;
(3)求参数,写出a,b的值,并求出c的值;
(4)写性质,按要求写出椭圆的简单几何性质.
探究一
探究二
探究三
素养形成
当堂检测
长、短轴长分别相等,且椭圆C2的焦点在y轴上.
(1)求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
(2)写出椭圆C2的方程,并研究其性质.
探究一
探究二
探究三
素养形成
当堂检测
根据椭圆的几何性质求其标准方程
例2根据下列条件求椭圆的标准方程:
(2)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为8.
思路分析:(1)焦点位置不确定,应分类讨论;(2)结合图形求出a,b,c的值代入.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),
且|OF|=c,|A1A2|=2b,
∴c=b=4,∴a2=b2+c2=32.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟根据椭圆的性质求方程
1.已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
2.在求椭圆方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2已知椭圆的长轴长是短轴长的2倍,且经过点A(2,0),求椭圆的标准方程.
探究一
探究二
探究三
素养形成
当堂检测
求椭圆的离心率的值(或范围)
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
(方法2)设A(0,b),B(a,0),F(-c,0),
设△FAB的外接圆的方程为x2+y2+Dx+Ey+F=0.
将A,B,F三点的坐标分别代入外接圆方程,
探究一
探究二
探究三
素养形成
当堂检测
答案:(1)A (2)A
探究一
探究二
探究三
素养形成
当堂检测
反思感悟求椭圆离心率及取值范围的两种方法
(2)方程法:若a,c的值不可求,则可根据条件建立a,b,c的关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程或不等式,再将方程或不等式两边同除以a的最高次幂,得到关于e的方程或不等式,即可求得e的值或范围.求离心率的范围时,应根据题意建立a,c的不等式,结合e∈(0,1)确定离心率的范围.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3(1)已知椭圆的焦距不小于短轴长,求椭圆的离心率的取值范围.
探究一
探究二
探究三
素养形成
当堂检测
(2)如图所示,设直线y=2x与椭圆的一个交点为P,
则点P横坐标为c,连接PF1,PF2,则|PF1|=2c.
因为△PF1F2为直角三角形,|F1F2|=2c,
探究一
探究二
探究三
素养形成
当堂检测
反思感悟离心率的求法
(3)若已知a,b,c的关系,则可转化为a,c的方程或不等式,进而得到关于e的方程或不等式进行求解.
探究一
探究二
探究三
素养形成
当堂检测
一题多变——求椭圆的离心率
答案:D
探究一
探究二
探究三
素养形成
当堂检测
变式训练1(变条件)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“∠PF2F1=75°,∠PF1F2=45°”,求椭圆C的离心率.
解:在△PF1F2中,
∵∠PF1F2=45°,∠PF2F1=75°,
∴∠F1PF2=60°,
设|PF1|=m,|PF2|=n,|F1F2|=2c,椭圆的长轴长为2a,
探究一
探究二
探究三
素养形成
当堂检测
变式训练2(变条件,变设问)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“椭圆C上存在点P,使∠F1PF2为钝角”,求椭圆C的离心率的取值范围.
探究一
探究二
探究三
素养形成
当堂检测
1.椭圆6x2+y2=6的长轴的端点坐标是( )
A.(-1,0),(1,0) B.(0,-1),(0,1)
答案:D
探究一
探究二
探究三
素养形成
当堂检测
答案:A
探究一
探究二
探究三
素养形成
当堂检测
答案:A
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
