人教A版(2019)高中数学选择性必修第一册 1.4.1 第1课时 空间中点、直线和平面的向量表示及空间中直线、平面的平行(48张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 1.4.1 第1课时 空间中点、直线和平面的向量表示及空间中直线、平面的平行(48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 18:37:49 | ||
图片预览










文档简介
1.4.1 用空间向量研究直线、平面的
位置关系
第1课时 空间中点、直线和平面的向量
表示及空间中直线、平面的平行
激趣诱思
知识点拨
牌楼与牌坊类似,是中国传统建筑之一,最早见于周朝.在园林、寺观、宫苑、陵墓和街道常有建造.旧时牌楼主要有木、石、木石、砖木、琉璃几种,多设于要道口.牌楼中有一种有柱门形构筑物,一般较高大.如图,牌楼的柱子与地面是垂直的,如果牌楼上部的下边线与柱子垂直,我们就能知道下边线与地面平行.
这是为什么呢?
激趣诱思
知识点拨
一、空间中点、直线和平面的向量表示
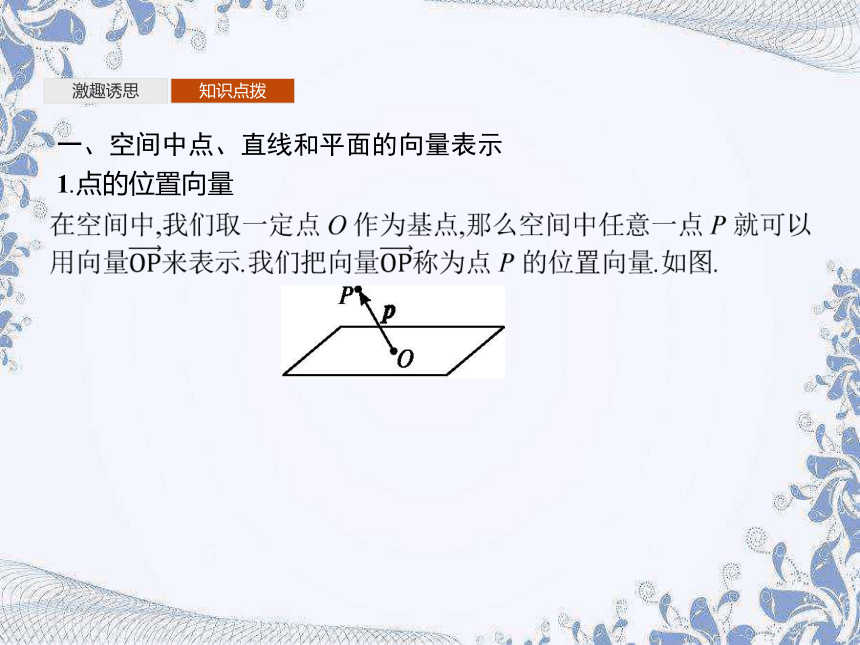
1.点的位置向量
激趣诱思
知识点拨
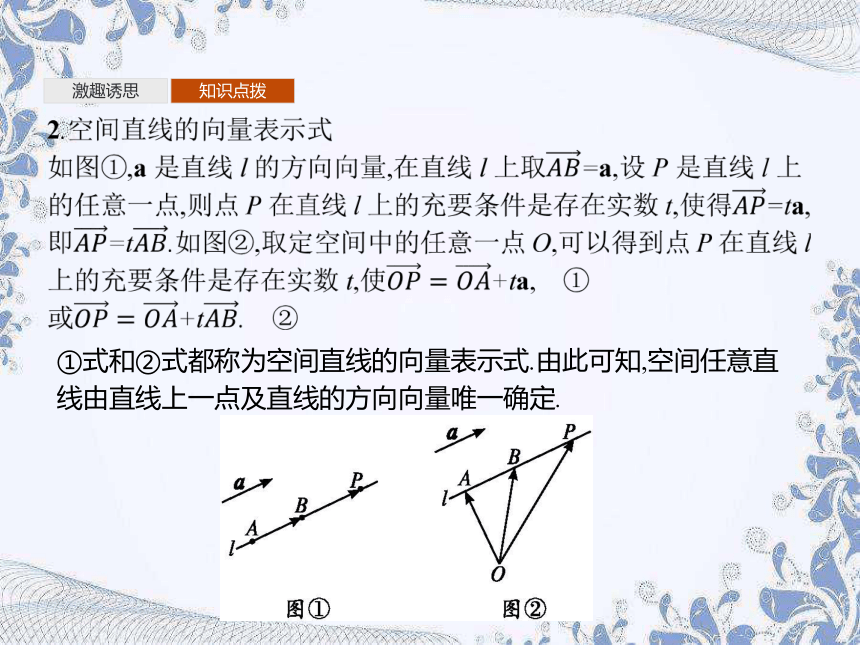
①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
激趣诱思
知识点拨
微练习1
下列说法中正确的是( )
A.直线的方向向量是唯一的
B.与一个平面的法向量共线的非零向量都是该平面的法向量
C.直线的方向向量有两个
D.平面的法向量是唯一的
答案:B
解析:由平面法向量的定义可知,B项正确.
激趣诱思
知识点拨
3.空间平面的向量表示式
激趣诱思
知识点拨
4.平面的法向量
如图,直线l⊥α,取直线l的方向向量a,我们称向量a为平面α的法向量.给定一个点A和一个向量a,那么过点A,且以向量a为法向量的平面完全确定,可以表示为集合
激趣诱思
知识点拨
名师点析1.空间中,一个向量成为直线l的方向向量,必须具备以下两个条件:①是非零向量;②向量所在的直线与l平行或重合.
激趣诱思
知识点拨
微练习2
若直线l过点A(-1,3,4),B(1,2,1),则直线l的一个方向向量可以是( )
答案:D
激趣诱思
知识点拨
微练习3
A.(-1,2,-1) B.(1,2,1)
C.(1,2,-1) D.(-1,2,1)
答案:A
令x=-1,则y=2,z=-1.
即平面ABC的一个法向量为n=(-1,2,-1).
激趣诱思
知识点拨
二、空间中直线、平面平行的向量表示
激趣诱思
知识点拨
名师点析1.空间平行关系的本质是线线平行,根据共线向量定理,只需证明直线的方向向量μ1∥μ2.此外,证明线面平行也可用共面向量定理,即只要证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可.
2.利用直线的方向向量证明直线与直线平行、直线与平面平行时,要注意向量所在的直线与所证直线或平面无公共点,证明平面与平面平行时也要注意两平面没有公共点.
激趣诱思
知识点拨
微练习1
若两条直线的方向向量分别是a=(2,4,-5),b=(-6,x,y),且两条直线平行,则x= ,y= .?
微练习2
若平面β外的一条直线l的方向向量是u=(-1,2,-3),平面β的法向量为n=(4,-1,-2),则l与β的位置关系是 .?
答案:-12 15
答案:平行
解析:因为u·n=(-1,2,-3)·(4,-1,-2)=0,
所以u⊥n.所以直线与平面平行,即l∥β.
探究一
探究二
探究三
探究四
素养形成
当堂检测
平面法向量及其求法
例1如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,求平面EDB的一个法向量.
思路分析首先建立空间直角坐标系,然后利用待定系数法按照平面法向量的求解步骤进行求解.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:如图所示建立空间直角坐标系.
依题意可得D(0,0,0),
P(0,0,1),
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟利用待定系数法求平面法向量的步骤
(1)设平面的法向量为n=(x,y,z).
(2)找出(求出)平面内的两个不共线的向量的坐标a=(a1,b1,c1),b=(a2,b2,c2).
(4)解方程组,取其中的一个解,即得法向量.
探究一
探究二
探究三
探究四
素养形成
当堂检测
延伸探究本例条件不变,你能分别求出平面PAD与平面PCD的一个法向量吗?它们之间的关系如何?
解:如同例题建系方法,易知平面PAD的一个法向量为n1=(0,1,0),平面PCD的一个法向量为n2=(1,0,0),因为n1·n2=0,所以n1⊥n2.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练1如图所示,已知四边形ABCD是直角梯形,AD∥BC,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD= ,试建立适当的坐标系.
(1)求平面ABCD的一个法向量;
(2)求平面SAB的一个法向量;
(3)求平面SCD的一个法向量.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:以点A为原点,AD、AB、AS所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用向量方法证明线线平行
例2在长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2,点P,Q,R,S分别是AA1,D1C1,AB,CC1的中点.求证:PQ∥RS.
证明: (方法1)以点D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系Dxyz.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟要证明两直线平行,可先求出两直线的方向向量,然后证明两直线的方向向量共线,从而证明两直线平行.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练2在正方体ABCD-A1B1C1D1中,点P在线段A1D上,点Q在线段AC上,线段PQ与直线A1D和AC都垂直,求证:PQ∥BD1.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:以点D为坐标原点,建立如图所示的空间直角坐标系,设正方体的棱长为1,
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用向量方法证明线面平行
例3如图,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
(方法3)以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图.
设正方体的棱长为1,则可求得
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟利用空间向量证明线面平行的方法
(1)利用共面向量法:证明直线的方向向量p与平面内的两个不共线向量a,b是共面向量,即满足p=xa+yb(x,y∈R),则p,a,b共面,从而可证直线与平面平行.
(2)利用共线向量法:证明直线的方向向量p与该平面内的某一向量共线,再结合线面平行的判定定理即可证明线面平行.
(3)利用法向量法:求出直线的方向向量与平面的法向量,证明方向向量与法向量垂直,从而证明直线与平面平行.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练3如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ,AF=1,M是线段EF的中点.求证:AM∥平面BDE.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:建立如图所示的空间直角坐标系.
设AC∩BD=N,连接NE,
又因为NE?平面BDE,AM?平面BDE,
所以AM∥平面BDE.
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用向量方法证明面面平行
例4如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?
思路分析建立空间直角坐标系,设出点Q的坐标,然后可根据面面平行的判定定理转化为向量共线问题或者利用两个平面的法向量共线进行证明.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:如图所示,分别以DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系,在CC1上任取一点Q,连接BQ,D1Q.
设正方体的棱长为1,
探究一
探究二
探究三
探究四
素养形成
当堂检测
故当Q为CC1的中点时,平面D1BQ∥平面PAO.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟利用空间向量证明面面平行的方法
(1)转化为线面平行、线线平行,然后借助向量共线进行证明;
(2)通过证明两个平面的法向量平行证明.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练4在长方体ABCD-A1B1C1D1中,DA=2,DC=3,DD1=4,
M,N,E,F分别为棱A1D1,A1B1,D1C1,B1C1的中点.
求证:平面AMN∥平面EFBD.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:建立如图所示的空间直角坐标系,
则A(2,0,0),B(2,3,0),
探究一
探究二
探究三
探究四
素养形成
当堂检测
一题多解——利用向量方法证明面面平行
典例如图,在正方体ABCD-A'B'C'D'中,求证:平面AB'D'∥平面BDC'.
解题提示证明面面平行常用的方法有两种,一是证明它们的法向量共线;二是转化为线面平行、线线平行即可.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:(方法1)设正方体的棱长为1,建立如图所示的空间直角坐标系,
则A(1,0,0),B'(1,1,1),
D'(0,0,1),B(1,1,0),D(0,0,0),C'(0,1,1),
令y1=1,则x1=-1,z1=-1,可得平面AB'D'的一个法向量为n1=(-1,1,-1).
设平面BDC'的法向量为n2=(x2,y2,z2).
探究一
探究二
探究三
探究四
素养形成
当堂检测
令y2=1,则x2=-1,z2=-1,可得平面BDC'的一个法向量为n2=(-1,1,-1).
所以n1=n2,所以n1∥n2,
故平面AB'D'∥平面BDC'.
即AD'∥BC',AB'∥DC',
所以AD'∥平面BDC',AB'∥平面BDC'.
又AD'∩AB'=A,所以平面AB'D'∥平面BDC'.
探究一
探究二
探究三
探究四
素养形成
当堂检测
所以n1也是平面BDC'的一个法向量,
所以平面AB'D'∥平面BDC'.
点评建立空间直角坐标系的关键是根据几何体的特征,尽可能找到三条两两互相垂直且相交于一点的线段,特别是有垂直关系的一些几何体,如正方体,长方体,直棱柱,有一条侧棱垂直于底面的棱锥等,其中长方体(或正方体)是最简单的模型.
探究一
探究二
探究三
探究四
素养形成
当堂检测
1.若不重合的直线l1,l2的方向向量分别为a=(1,2,-2),b=(-3,-6,6),则( )
A.l1∥l2 B.l1⊥l2
C.l1,l2相交但不垂直 D.不能确定
答案:A
探究一
探究二
探究三
探究四
素养形成
当堂检测
2.已知线段AB的两端点坐标为A(9,-3,4),B(9,2,1),则直线AB( )
A.与坐标平面xOy平行
B.与坐标平面yOz平行
C.与坐标平面xOz平行
D.与坐标平面yOz相交
答案:B
解析:因为A(9,-3,4),B(9,2,1),所以 =(0,5,-3),而坐标平面yOz的法向量为(1,0,0),显然(0,5,-3)·(1,0,0)=0,故直线AB与坐标平面yOz平行.
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.若平面α∥β,则下面可以是这两个平面法向量的是( )
A.n1=(1,2,3),n2=(-3,2,1)
B.n1=(1,2,2),n2=(-2,2,1)
C.n1=(1,1,1),n2=(-2,2,1)
D.n1=(1,1,1),n2=(-2,-2,-2)
答案:D
解析:因为平面α∥β,所以两个平面的法向量应该平行,只有D项符合.
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:-8
探究一
探究二
探究三
探究四
素养形成
当堂检测
5.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是BB1,DD1的中点,求证:
(1)FC1∥平面ADE;
(2)平面ADE∥平面B1C1F.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:如图,建立空间直角坐标系Dxyz,
则D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2),
探究一
探究二
探究三
探究四
素养形成
当堂检测
位置关系
第1课时 空间中点、直线和平面的向量
表示及空间中直线、平面的平行
激趣诱思
知识点拨
牌楼与牌坊类似,是中国传统建筑之一,最早见于周朝.在园林、寺观、宫苑、陵墓和街道常有建造.旧时牌楼主要有木、石、木石、砖木、琉璃几种,多设于要道口.牌楼中有一种有柱门形构筑物,一般较高大.如图,牌楼的柱子与地面是垂直的,如果牌楼上部的下边线与柱子垂直,我们就能知道下边线与地面平行.
这是为什么呢?
激趣诱思
知识点拨
一、空间中点、直线和平面的向量表示
1.点的位置向量
激趣诱思
知识点拨
①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
激趣诱思
知识点拨
微练习1
下列说法中正确的是( )
A.直线的方向向量是唯一的
B.与一个平面的法向量共线的非零向量都是该平面的法向量
C.直线的方向向量有两个
D.平面的法向量是唯一的
答案:B
解析:由平面法向量的定义可知,B项正确.
激趣诱思
知识点拨
3.空间平面的向量表示式
激趣诱思
知识点拨
4.平面的法向量
如图,直线l⊥α,取直线l的方向向量a,我们称向量a为平面α的法向量.给定一个点A和一个向量a,那么过点A,且以向量a为法向量的平面完全确定,可以表示为集合
激趣诱思
知识点拨
名师点析1.空间中,一个向量成为直线l的方向向量,必须具备以下两个条件:①是非零向量;②向量所在的直线与l平行或重合.
激趣诱思
知识点拨
微练习2
若直线l过点A(-1,3,4),B(1,2,1),则直线l的一个方向向量可以是( )
答案:D
激趣诱思
知识点拨
微练习3
A.(-1,2,-1) B.(1,2,1)
C.(1,2,-1) D.(-1,2,1)
答案:A
令x=-1,则y=2,z=-1.
即平面ABC的一个法向量为n=(-1,2,-1).
激趣诱思
知识点拨
二、空间中直线、平面平行的向量表示
激趣诱思
知识点拨
名师点析1.空间平行关系的本质是线线平行,根据共线向量定理,只需证明直线的方向向量μ1∥μ2.此外,证明线面平行也可用共面向量定理,即只要证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可.
2.利用直线的方向向量证明直线与直线平行、直线与平面平行时,要注意向量所在的直线与所证直线或平面无公共点,证明平面与平面平行时也要注意两平面没有公共点.
激趣诱思
知识点拨
微练习1
若两条直线的方向向量分别是a=(2,4,-5),b=(-6,x,y),且两条直线平行,则x= ,y= .?
微练习2
若平面β外的一条直线l的方向向量是u=(-1,2,-3),平面β的法向量为n=(4,-1,-2),则l与β的位置关系是 .?
答案:-12 15
答案:平行
解析:因为u·n=(-1,2,-3)·(4,-1,-2)=0,
所以u⊥n.所以直线与平面平行,即l∥β.
探究一
探究二
探究三
探究四
素养形成
当堂检测
平面法向量及其求法
例1如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,求平面EDB的一个法向量.
思路分析首先建立空间直角坐标系,然后利用待定系数法按照平面法向量的求解步骤进行求解.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:如图所示建立空间直角坐标系.
依题意可得D(0,0,0),
P(0,0,1),
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟利用待定系数法求平面法向量的步骤
(1)设平面的法向量为n=(x,y,z).
(2)找出(求出)平面内的两个不共线的向量的坐标a=(a1,b1,c1),b=(a2,b2,c2).
(4)解方程组,取其中的一个解,即得法向量.
探究一
探究二
探究三
探究四
素养形成
当堂检测
延伸探究本例条件不变,你能分别求出平面PAD与平面PCD的一个法向量吗?它们之间的关系如何?
解:如同例题建系方法,易知平面PAD的一个法向量为n1=(0,1,0),平面PCD的一个法向量为n2=(1,0,0),因为n1·n2=0,所以n1⊥n2.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练1如图所示,已知四边形ABCD是直角梯形,AD∥BC,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD= ,试建立适当的坐标系.
(1)求平面ABCD的一个法向量;
(2)求平面SAB的一个法向量;
(3)求平面SCD的一个法向量.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:以点A为原点,AD、AB、AS所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用向量方法证明线线平行
例2在长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2,点P,Q,R,S分别是AA1,D1C1,AB,CC1的中点.求证:PQ∥RS.
证明: (方法1)以点D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系Dxyz.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟要证明两直线平行,可先求出两直线的方向向量,然后证明两直线的方向向量共线,从而证明两直线平行.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练2在正方体ABCD-A1B1C1D1中,点P在线段A1D上,点Q在线段AC上,线段PQ与直线A1D和AC都垂直,求证:PQ∥BD1.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:以点D为坐标原点,建立如图所示的空间直角坐标系,设正方体的棱长为1,
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用向量方法证明线面平行
例3如图,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
探究一
探究二
探究三
探究四
素养形成
当堂检测
探究一
探究二
探究三
探究四
素养形成
当堂检测
(方法3)以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图.
设正方体的棱长为1,则可求得
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟利用空间向量证明线面平行的方法
(1)利用共面向量法:证明直线的方向向量p与平面内的两个不共线向量a,b是共面向量,即满足p=xa+yb(x,y∈R),则p,a,b共面,从而可证直线与平面平行.
(2)利用共线向量法:证明直线的方向向量p与该平面内的某一向量共线,再结合线面平行的判定定理即可证明线面平行.
(3)利用法向量法:求出直线的方向向量与平面的法向量,证明方向向量与法向量垂直,从而证明直线与平面平行.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练3如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ,AF=1,M是线段EF的中点.求证:AM∥平面BDE.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:建立如图所示的空间直角坐标系.
设AC∩BD=N,连接NE,
又因为NE?平面BDE,AM?平面BDE,
所以AM∥平面BDE.
探究一
探究二
探究三
探究四
素养形成
当堂检测
利用向量方法证明面面平行
例4如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?
思路分析建立空间直角坐标系,设出点Q的坐标,然后可根据面面平行的判定定理转化为向量共线问题或者利用两个平面的法向量共线进行证明.
探究一
探究二
探究三
探究四
素养形成
当堂检测
解:如图所示,分别以DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系,在CC1上任取一点Q,连接BQ,D1Q.
设正方体的棱长为1,
探究一
探究二
探究三
探究四
素养形成
当堂检测
故当Q为CC1的中点时,平面D1BQ∥平面PAO.
探究一
探究二
探究三
探究四
素养形成
当堂检测
反思感悟利用空间向量证明面面平行的方法
(1)转化为线面平行、线线平行,然后借助向量共线进行证明;
(2)通过证明两个平面的法向量平行证明.
探究一
探究二
探究三
探究四
素养形成
当堂检测
变式训练4在长方体ABCD-A1B1C1D1中,DA=2,DC=3,DD1=4,
M,N,E,F分别为棱A1D1,A1B1,D1C1,B1C1的中点.
求证:平面AMN∥平面EFBD.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:建立如图所示的空间直角坐标系,
则A(2,0,0),B(2,3,0),
探究一
探究二
探究三
探究四
素养形成
当堂检测
一题多解——利用向量方法证明面面平行
典例如图,在正方体ABCD-A'B'C'D'中,求证:平面AB'D'∥平面BDC'.
解题提示证明面面平行常用的方法有两种,一是证明它们的法向量共线;二是转化为线面平行、线线平行即可.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:(方法1)设正方体的棱长为1,建立如图所示的空间直角坐标系,
则A(1,0,0),B'(1,1,1),
D'(0,0,1),B(1,1,0),D(0,0,0),C'(0,1,1),
令y1=1,则x1=-1,z1=-1,可得平面AB'D'的一个法向量为n1=(-1,1,-1).
设平面BDC'的法向量为n2=(x2,y2,z2).
探究一
探究二
探究三
探究四
素养形成
当堂检测
令y2=1,则x2=-1,z2=-1,可得平面BDC'的一个法向量为n2=(-1,1,-1).
所以n1=n2,所以n1∥n2,
故平面AB'D'∥平面BDC'.
即AD'∥BC',AB'∥DC',
所以AD'∥平面BDC',AB'∥平面BDC'.
又AD'∩AB'=A,所以平面AB'D'∥平面BDC'.
探究一
探究二
探究三
探究四
素养形成
当堂检测
所以n1也是平面BDC'的一个法向量,
所以平面AB'D'∥平面BDC'.
点评建立空间直角坐标系的关键是根据几何体的特征,尽可能找到三条两两互相垂直且相交于一点的线段,特别是有垂直关系的一些几何体,如正方体,长方体,直棱柱,有一条侧棱垂直于底面的棱锥等,其中长方体(或正方体)是最简单的模型.
探究一
探究二
探究三
探究四
素养形成
当堂检测
1.若不重合的直线l1,l2的方向向量分别为a=(1,2,-2),b=(-3,-6,6),则( )
A.l1∥l2 B.l1⊥l2
C.l1,l2相交但不垂直 D.不能确定
答案:A
探究一
探究二
探究三
探究四
素养形成
当堂检测
2.已知线段AB的两端点坐标为A(9,-3,4),B(9,2,1),则直线AB( )
A.与坐标平面xOy平行
B.与坐标平面yOz平行
C.与坐标平面xOz平行
D.与坐标平面yOz相交
答案:B
解析:因为A(9,-3,4),B(9,2,1),所以 =(0,5,-3),而坐标平面yOz的法向量为(1,0,0),显然(0,5,-3)·(1,0,0)=0,故直线AB与坐标平面yOz平行.
探究一
探究二
探究三
探究四
素养形成
当堂检测
3.若平面α∥β,则下面可以是这两个平面法向量的是( )
A.n1=(1,2,3),n2=(-3,2,1)
B.n1=(1,2,2),n2=(-2,2,1)
C.n1=(1,1,1),n2=(-2,2,1)
D.n1=(1,1,1),n2=(-2,-2,-2)
答案:D
解析:因为平面α∥β,所以两个平面的法向量应该平行,只有D项符合.
探究一
探究二
探究三
探究四
素养形成
当堂检测
答案:-8
探究一
探究二
探究三
探究四
素养形成
当堂检测
5.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是BB1,DD1的中点,求证:
(1)FC1∥平面ADE;
(2)平面ADE∥平面B1C1F.
探究一
探究二
探究三
探究四
素养形成
当堂检测
证明:如图,建立空间直角坐标系Dxyz,
则D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2),
探究一
探究二
探究三
探究四
素养形成
当堂检测
