人教A版(2019)高中数学选择性必修第一册 2.1.1 倾斜角与斜率(24张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 2.1.1 倾斜角与斜率(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 999.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览







文档简介
2.1.1 倾斜角与斜率
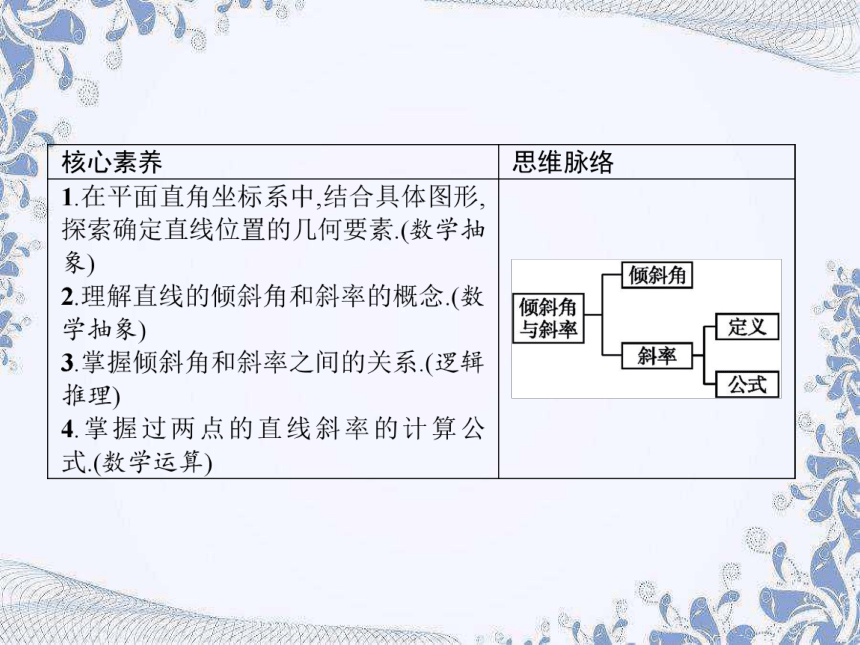
激趣诱思
知识点拨
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值
了实际应用与安全,在道路铺设时常要规划坡度的大小.那么“坡度”是如何来刻画道路的倾斜程度的呢?
激趣诱思
知识点拨
一、直线的倾斜角
激趣诱思
知识点拨
名师点析倾斜角还可以这样定义:在平面直角坐标系中,对于一条与x轴相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到和直线重合时所转过的最小正角称为这条直线的倾斜角.并规定:与x轴平行或重合的直线的倾斜角为0°.
激趣诱思
知识点拨
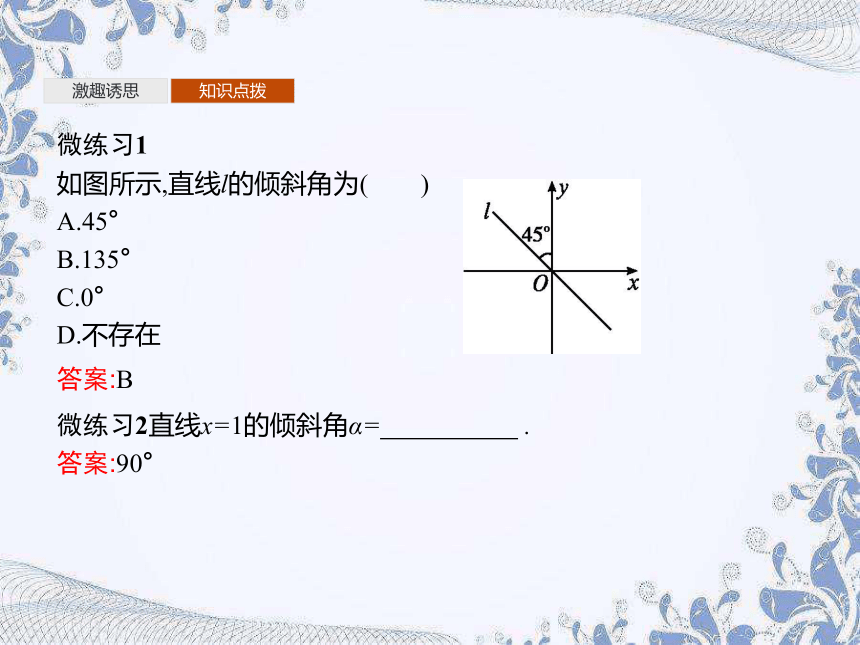
微练习1
如图所示,直线l的倾斜角为( )
A.45°
B.135°
C.0°
D.不存在
答案:B
微练习2直线x=1的倾斜角α= .
答案:90°
激趣诱思
知识点拨
二、直线的斜率
1.定义与表示
激趣诱思
知识点拨
2.填表:斜率与倾斜角的对应关系
激趣诱思
知识点拨
微思考1
任何一条直线都有倾斜角吗?任何一条直线都有斜率吗?
答案:任何一条直线都有倾斜角.但倾斜角为90°的直线没有斜率.
微思考2
直线的倾斜角越大,斜率就越大吗?
微练习
已知直线l的斜率k=-1,则其倾斜角α= .?
答案:135°
激趣诱思
知识点拨
三、直线的斜率公式
如果直线经过两点P1(x1,y1),P2(x2,y2),(x1≠x2),则直线的斜率公式为
名师点析1.运用公式的前提是x1≠x2,即直线不与x轴垂直.
2.斜率公式与P1,P2在直线上的位置无关,在直线上任取两点,得到的斜率是相同的.
3.需注意公式中横、纵坐标之差的顺序,也可以写成
即下标的顺序一致.
激趣诱思
知识点拨
微练习
已知点P1(3,5),P2(-1,-3),则直线P1P2的斜率k等于( )
A.2
B.1
D.不存在
答案:A
探究一
探究二
素养形成
当堂检测
直线的倾斜角
例1已知直线l过原点,l绕原点按顺时针方向转动角α(0°<α<180°)后,恰好与y轴重合,求直线l转动前的倾斜角是多少?
思路分析:画草图→标记α→找倾斜角与α的关系→求倾斜角
解:由题意画出如下草图.
由图可知:
当α为钝角时,倾斜角为α-90°,
当α为锐角时,倾斜角为α+90°,
当α为直角时,倾斜角为0°.
探究一
探究二
素养形成
当堂检测
反思感悟直线的倾斜角的求法
求直线的倾斜角主要根据定义,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
探究一
探究二
素养形成
当堂检测
变式训练设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角为( )
A.α+45°
B.α-135°
C.135°-α
D.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α-135°
探究一
探究二
素养形成
当堂检测
解析:根据题意,画出图形,如图所示:
因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.通过画图(如图所示)可知:当0°≤α<135°时,l1的倾斜角为α+45°;当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.故选D.
答案:D
探究一
探究二
素养形成
当堂检测
斜率公式及其应用
例2已知直线l过点M(m+1,m-1),N(2m,1).
(1)当m为何值时,直线l的斜率是1?
(2)当m为何值时,直线l的倾斜角为90°?
思路分析:求直线的斜率?直线的斜率公式.
(2)l的倾斜角为90°,即l平行于y轴,所以m+1=2m,得m=1.
反思感悟直线斜率的计算方法
(1)判断两点的横坐标是否相等,若相等,则直线的斜率不存在.
探究一
探究二
素养形成
当堂检测
延伸探究1本例条件不变,试求直线l的倾斜角为锐角时实数m的取值范围.
探究一
探究二
素养形成
当堂检测
延伸探究2若将本例中的“N(2m,1)”改为“N(3m,2m)”,其他条件不变,结果如何?
探究一
探究二
素养形成
当堂检测
一题多解——利用斜率解决反射问题
典例光线从点A(2,1)射到y轴上的点Q,经y轴反射后过点B(4,3),试求点Q的坐标及入射光线的斜率.
(方法2)设Q(0,y),如图,点B(4,3)关于y轴的对称点为B'(-4,3),
探究一
探究二
素养形成
当堂检测
方法总结光的反射问题中,反射角等于入射角,但反射光线的斜率并不等于入射光线的斜率.当镜面水平放置时,它们之间是互为相反数的关系.另外,在光的反射问题中也经常使用对称的方法求解.
探究一
探究二
素养形成
当堂检测
变式训练一束光线从点A(-2,3)射入,经x轴上点P反射后,通过点B(5,7),求点P的坐标.
探究一
探究二
素养形成
当堂检测
1.若直线l经过第二、第四象限,则直线l的倾斜角范围是( )
A.0°≤α<90° B.90°≤α<180°
C.90°<α<180° D.0°<α<180°
答案:C
答案:A
探究一
探究二
素养形成
当堂检测
3.过点P(-2,m),Q(m,4)的直线的斜率为1,那么m的值为( )
A.1或4 B.4
C.1或3 D.1
答案:D
探究一
探究二
素养形成
当堂检测
答案:60°
激趣诱思
知识点拨
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值
了实际应用与安全,在道路铺设时常要规划坡度的大小.那么“坡度”是如何来刻画道路的倾斜程度的呢?
激趣诱思
知识点拨
一、直线的倾斜角
激趣诱思
知识点拨
名师点析倾斜角还可以这样定义:在平面直角坐标系中,对于一条与x轴相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到和直线重合时所转过的最小正角称为这条直线的倾斜角.并规定:与x轴平行或重合的直线的倾斜角为0°.
激趣诱思
知识点拨
微练习1
如图所示,直线l的倾斜角为( )
A.45°
B.135°
C.0°
D.不存在
答案:B
微练习2直线x=1的倾斜角α= .
答案:90°
激趣诱思
知识点拨
二、直线的斜率
1.定义与表示
激趣诱思
知识点拨
2.填表:斜率与倾斜角的对应关系
激趣诱思
知识点拨
微思考1
任何一条直线都有倾斜角吗?任何一条直线都有斜率吗?
答案:任何一条直线都有倾斜角.但倾斜角为90°的直线没有斜率.
微思考2
直线的倾斜角越大,斜率就越大吗?
微练习
已知直线l的斜率k=-1,则其倾斜角α= .?
答案:135°
激趣诱思
知识点拨
三、直线的斜率公式
如果直线经过两点P1(x1,y1),P2(x2,y2),(x1≠x2),则直线的斜率公式为
名师点析1.运用公式的前提是x1≠x2,即直线不与x轴垂直.
2.斜率公式与P1,P2在直线上的位置无关,在直线上任取两点,得到的斜率是相同的.
3.需注意公式中横、纵坐标之差的顺序,也可以写成
即下标的顺序一致.
激趣诱思
知识点拨
微练习
已知点P1(3,5),P2(-1,-3),则直线P1P2的斜率k等于( )
A.2
B.1
D.不存在
答案:A
探究一
探究二
素养形成
当堂检测
直线的倾斜角
例1已知直线l过原点,l绕原点按顺时针方向转动角α(0°<α<180°)后,恰好与y轴重合,求直线l转动前的倾斜角是多少?
思路分析:画草图→标记α→找倾斜角与α的关系→求倾斜角
解:由题意画出如下草图.
由图可知:
当α为钝角时,倾斜角为α-90°,
当α为锐角时,倾斜角为α+90°,
当α为直角时,倾斜角为0°.
探究一
探究二
素养形成
当堂检测
反思感悟直线的倾斜角的求法
求直线的倾斜角主要根据定义,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
探究一
探究二
素养形成
当堂检测
变式训练设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角为( )
A.α+45°
B.α-135°
C.135°-α
D.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α-135°
探究一
探究二
素养形成
当堂检测
解析:根据题意,画出图形,如图所示:
因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.通过画图(如图所示)可知:当0°≤α<135°时,l1的倾斜角为α+45°;当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.故选D.
答案:D
探究一
探究二
素养形成
当堂检测
斜率公式及其应用
例2已知直线l过点M(m+1,m-1),N(2m,1).
(1)当m为何值时,直线l的斜率是1?
(2)当m为何值时,直线l的倾斜角为90°?
思路分析:求直线的斜率?直线的斜率公式.
(2)l的倾斜角为90°,即l平行于y轴,所以m+1=2m,得m=1.
反思感悟直线斜率的计算方法
(1)判断两点的横坐标是否相等,若相等,则直线的斜率不存在.
探究一
探究二
素养形成
当堂检测
延伸探究1本例条件不变,试求直线l的倾斜角为锐角时实数m的取值范围.
探究一
探究二
素养形成
当堂检测
延伸探究2若将本例中的“N(2m,1)”改为“N(3m,2m)”,其他条件不变,结果如何?
探究一
探究二
素养形成
当堂检测
一题多解——利用斜率解决反射问题
典例光线从点A(2,1)射到y轴上的点Q,经y轴反射后过点B(4,3),试求点Q的坐标及入射光线的斜率.
(方法2)设Q(0,y),如图,点B(4,3)关于y轴的对称点为B'(-4,3),
探究一
探究二
素养形成
当堂检测
方法总结光的反射问题中,反射角等于入射角,但反射光线的斜率并不等于入射光线的斜率.当镜面水平放置时,它们之间是互为相反数的关系.另外,在光的反射问题中也经常使用对称的方法求解.
探究一
探究二
素养形成
当堂检测
变式训练一束光线从点A(-2,3)射入,经x轴上点P反射后,通过点B(5,7),求点P的坐标.
探究一
探究二
素养形成
当堂检测
1.若直线l经过第二、第四象限,则直线l的倾斜角范围是( )
A.0°≤α<90° B.90°≤α<180°
C.90°<α<180° D.0°<α<180°
答案:C
答案:A
探究一
探究二
素养形成
当堂检测
3.过点P(-2,m),Q(m,4)的直线的斜率为1,那么m的值为( )
A.1或4 B.4
C.1或3 D.1
答案:D
探究一
探究二
素养形成
当堂检测
答案:60°
