人教A版(2019)高中数学选择性必修第二册 4.3.2 第1课时 等比数列的前n项和(24张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 4.3.2 第1课时 等比数列的前n项和(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 974.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览








文档简介
4.3.2 等比数列的前n项和公式
第1课时 等比数列的前n项和
激趣诱思
知识点拨
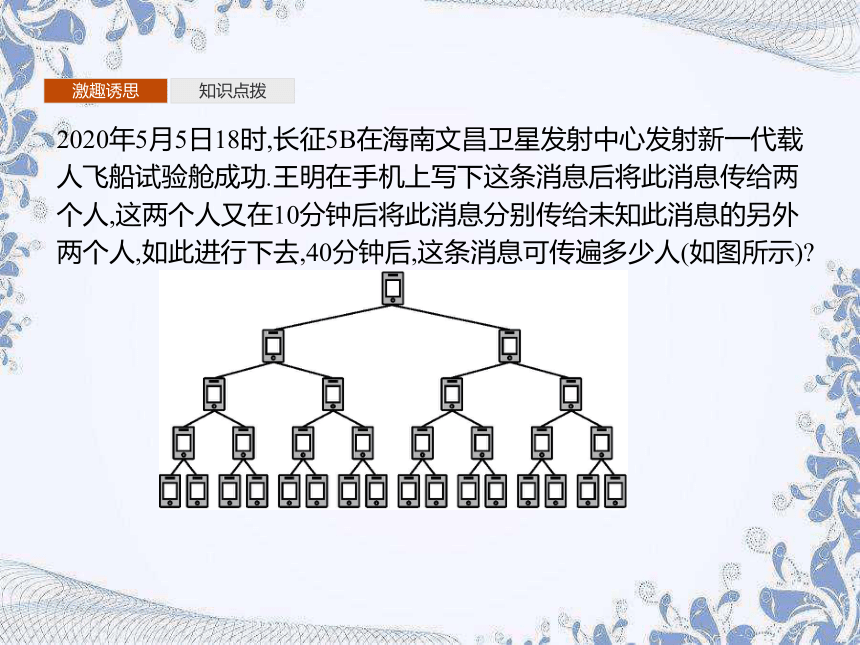
2020年5月5日18时,长征5B在海南文昌卫星发射中心发射新一代载人飞船试验舱成功.王明在手机上写下这条消息后将此消息传给两个人,这两个人又在10分钟后将此消息分别传给未知此消息的另外两个人,如此进行下去,40分钟后,这条消息可传遍多少人(如图所示)?
激趣诱思
知识点拨
一、等比数列的前n项和公式
若等比数列的首项为a1,公比为q,则它的前n项和
名师点析(1)当等比数列的公比q为字母时,求等比数列的前n项和公式常需分q=1与q≠1两种情况,因此当等比数列的公比未知或是代数式时,要对公比进行分类讨论.
激趣诱思
知识点拨
微练习
(1)在等比数列{an}中,Sn为其前n项和,若a1=3,q=4,则S5= .?
(2)在等比数列{an}中,Sn为其前n项和,若a1= ,a6=16,则S6= .?
激趣诱思
知识点拨
二、错位相减法求数列的和
推导等比数列前n项和的方法叫做错位相减法,一般适用于求一个等差数列与一个等比数列对应项的积所构成的数列的前n项和.
微练习
下列数列中,可以用错位相减法求和的是( )
解析:C项中的数列是一个等差数列与一个等比数列对应项的积构成的,故可用错位相减法求和.
答案:C
探究一
探究二
素养形成
当堂检测
等比数列前n项和公式的应用
例1在等比数列{an}中,Sn为其前n项和,解决下列问题:
(1)若an=3×2n,求S6;
(2)若a1+a3=10,a4+a6= ,求S5;
(3)若Sn=189,q=2,an=96,求a1和n.
分析:先利用等比数列前n项和公式直接计算或建立方程组求得基本量,再代入计算.
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
反思感悟等比数列前n项和公式的应用问题
在等比数列{an}的五个量a1,q,an,n,Sn中,a1与q是最基本的元素,当条件与结论间的联系不明显时,均可以用a1与q表示an与Sn,从而列方程组求解.在解方程组时经常用到两式相除达到整体消元的目的.这是方程思想与整体思想在数列中的具体应用.
探究一
探究二
素养形成
当堂检测
变式训练1(1)设等比数列{an}的公比q=2,前n项和为Sn,则
探究一
探究二
素养形成
当堂检测
例2设等比数列{an}的前n项和为Sn,若S2+S4=S6,求其公比q.
分析:可根据前n项和公式建立公比q的方程求解,但必须先对q的值分q=1和q≠1进行分类讨论.
解:(1)若q=1,则S2=2a1,S4=4a1,S6=6a1,显然满足S2+S4=S6,所以q=1符合题意;
得(q2+1)(q+1)2(q-1)2=0,解得q=-1(q=1舍去).综上,公比q的值等于1或-1.
反思感悟等比数列前n项和公式的关注点
在利用等比数列的前n项和公式时,若其公比不确定,则应对公比分q=1和q≠1两种情况分别进行讨论.
探究一
探究二
素养形成
当堂检测
延伸探究本例中,若条件改为“数列{an}是等比数列,其前n项和为Sn,且S3=3a3”,求其公比q的值.
探究一
探究二
素养形成
当堂检测
错位相减法求和
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
反思感悟错位相减法求和的解题策略
1.如果一个数列的各项是由一个等差数列和一个等比数列对应项乘积组成,此时可把式子Sn=a1+a2+…+an两边同乘公比q,得到qSn=a1q+a2q+…+anq,两式错位相减整理即可求出Sn.
2.错位相减法求和是一种非常重要的求和方法,这种方法的计算过程较为复杂,对计算能力要求较高,应加强训练.要注意通过训练,掌握在错位相减过程中的几个关键环节,避免出错.
探究一
探究二
素养形成
当堂检测
变式训练2已知数列{an}是首项、公比都为5的等比数列,bn=anlog25an(n∈N*),求数列{bn}的前n项和Sn.
探究一
探究二
素养形成
当堂检测
分类讨论法求等比数列的前n项和
典例求数列1,2a,4a2,8a3,…的前n项和Sn.
解:(1)当a=0时,易得数列的前n项和Sn=1.
(2)当a≠0时,数列是公比为2a的等比数列.
探究一
探究二
素养形成
当堂检测
防范措施等比数列与等差数列相比,具有更多的特殊性,例如,等比数列中的任何一项均不能为零,等比数列的求和公式中,要分q=1和q≠1两种情况分别求解,因此当等比数列中的项含有字母时,要注意分类讨论.
探究一
探究二
素养形成
当堂检测
1.在等比数列{an}中,其前n项和为Sn,a1=5,S5=55,则公比q等于( )
A.4 B.2
C.-2 D.-2或4
代入上式验证得q=-2.
答案:C
探究一
探究二
素养形成
当堂检测
2.在公比为整数的等比数列{an}中,如果a1+a4=18,a2+a3=12,那么该数列的前8项和为( )
答案:C
探究一
探究二
素养形成
当堂检测
3.(2019全国Ⅰ,理14)记Sn为等比数列{an}的前n项和.若
探究一
探究二
素养形成
当堂检测
答案:15
5.求数列an=n·2n的前n项和.
解:设前n项和为Sn,则Sn=1×21+2×22+3×23+…+n·2n,则2Sn=1×22+2×23+3×24+…+(n-1)·2n+n·2n+1,两式相减,得-Sn=1×21+(22+23+24+…+2n)-n·2n+1,
故Sn=(n-1)·2n+1+2.
第1课时 等比数列的前n项和
激趣诱思
知识点拨
2020年5月5日18时,长征5B在海南文昌卫星发射中心发射新一代载人飞船试验舱成功.王明在手机上写下这条消息后将此消息传给两个人,这两个人又在10分钟后将此消息分别传给未知此消息的另外两个人,如此进行下去,40分钟后,这条消息可传遍多少人(如图所示)?
激趣诱思
知识点拨
一、等比数列的前n项和公式
若等比数列的首项为a1,公比为q,则它的前n项和
名师点析(1)当等比数列的公比q为字母时,求等比数列的前n项和公式常需分q=1与q≠1两种情况,因此当等比数列的公比未知或是代数式时,要对公比进行分类讨论.
激趣诱思
知识点拨
微练习
(1)在等比数列{an}中,Sn为其前n项和,若a1=3,q=4,则S5= .?
(2)在等比数列{an}中,Sn为其前n项和,若a1= ,a6=16,则S6= .?
激趣诱思
知识点拨
二、错位相减法求数列的和
推导等比数列前n项和的方法叫做错位相减法,一般适用于求一个等差数列与一个等比数列对应项的积所构成的数列的前n项和.
微练习
下列数列中,可以用错位相减法求和的是( )
解析:C项中的数列是一个等差数列与一个等比数列对应项的积构成的,故可用错位相减法求和.
答案:C
探究一
探究二
素养形成
当堂检测
等比数列前n项和公式的应用
例1在等比数列{an}中,Sn为其前n项和,解决下列问题:
(1)若an=3×2n,求S6;
(2)若a1+a3=10,a4+a6= ,求S5;
(3)若Sn=189,q=2,an=96,求a1和n.
分析:先利用等比数列前n项和公式直接计算或建立方程组求得基本量,再代入计算.
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
反思感悟等比数列前n项和公式的应用问题
在等比数列{an}的五个量a1,q,an,n,Sn中,a1与q是最基本的元素,当条件与结论间的联系不明显时,均可以用a1与q表示an与Sn,从而列方程组求解.在解方程组时经常用到两式相除达到整体消元的目的.这是方程思想与整体思想在数列中的具体应用.
探究一
探究二
素养形成
当堂检测
变式训练1(1)设等比数列{an}的公比q=2,前n项和为Sn,则
探究一
探究二
素养形成
当堂检测
例2设等比数列{an}的前n项和为Sn,若S2+S4=S6,求其公比q.
分析:可根据前n项和公式建立公比q的方程求解,但必须先对q的值分q=1和q≠1进行分类讨论.
解:(1)若q=1,则S2=2a1,S4=4a1,S6=6a1,显然满足S2+S4=S6,所以q=1符合题意;
得(q2+1)(q+1)2(q-1)2=0,解得q=-1(q=1舍去).综上,公比q的值等于1或-1.
反思感悟等比数列前n项和公式的关注点
在利用等比数列的前n项和公式时,若其公比不确定,则应对公比分q=1和q≠1两种情况分别进行讨论.
探究一
探究二
素养形成
当堂检测
延伸探究本例中,若条件改为“数列{an}是等比数列,其前n项和为Sn,且S3=3a3”,求其公比q的值.
探究一
探究二
素养形成
当堂检测
错位相减法求和
探究一
探究二
素养形成
当堂检测
探究一
探究二
素养形成
当堂检测
反思感悟错位相减法求和的解题策略
1.如果一个数列的各项是由一个等差数列和一个等比数列对应项乘积组成,此时可把式子Sn=a1+a2+…+an两边同乘公比q,得到qSn=a1q+a2q+…+anq,两式错位相减整理即可求出Sn.
2.错位相减法求和是一种非常重要的求和方法,这种方法的计算过程较为复杂,对计算能力要求较高,应加强训练.要注意通过训练,掌握在错位相减过程中的几个关键环节,避免出错.
探究一
探究二
素养形成
当堂检测
变式训练2已知数列{an}是首项、公比都为5的等比数列,bn=anlog25an(n∈N*),求数列{bn}的前n项和Sn.
探究一
探究二
素养形成
当堂检测
分类讨论法求等比数列的前n项和
典例求数列1,2a,4a2,8a3,…的前n项和Sn.
解:(1)当a=0时,易得数列的前n项和Sn=1.
(2)当a≠0时,数列是公比为2a的等比数列.
探究一
探究二
素养形成
当堂检测
防范措施等比数列与等差数列相比,具有更多的特殊性,例如,等比数列中的任何一项均不能为零,等比数列的求和公式中,要分q=1和q≠1两种情况分别求解,因此当等比数列中的项含有字母时,要注意分类讨论.
探究一
探究二
素养形成
当堂检测
1.在等比数列{an}中,其前n项和为Sn,a1=5,S5=55,则公比q等于( )
A.4 B.2
C.-2 D.-2或4
代入上式验证得q=-2.
答案:C
探究一
探究二
素养形成
当堂检测
2.在公比为整数的等比数列{an}中,如果a1+a4=18,a2+a3=12,那么该数列的前8项和为( )
答案:C
探究一
探究二
素养形成
当堂检测
3.(2019全国Ⅰ,理14)记Sn为等比数列{an}的前n项和.若
探究一
探究二
素养形成
当堂检测
答案:15
5.求数列an=n·2n的前n项和.
解:设前n项和为Sn,则Sn=1×21+2×22+3×23+…+n·2n,则2Sn=1×22+2×23+3×24+…+(n-1)·2n+n·2n+1,两式相减,得-Sn=1×21+(22+23+24+…+2n)-n·2n+1,
故Sn=(n-1)·2n+1+2.
