人教A版(2019)高中数学选择性必修第二册 5.2.3 简单复合函数的导数(27张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 5.2.3 简单复合函数的导数(27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 18:18:38 | ||
图片预览








文档简介
5.2.3 简单复合函数的导数
激趣诱思
知识点拨
我们学习过基本初等函数,如指数函数、对数函数、幂函数、三角函数、常数函数,我们可以把这些函数进行加、减、乘、除、乘方、开方等运算得到新的函数,还有一种构造新函数的方法,那就是把两个或几个函数“复合”起来,怎样“复合”呢,复合后的函数怎样求导呢?本节课就让我们来解决这些问题.
激趣诱思
知识点拨
1.复合函数的概念
一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).
2.复合函数的求导法则
一般地,对于由函数y=f(u)和u=g(x)复合而成的函数y=f(g(x)),它的导数与函数y=f(u),u=g(x)的导数间的关系为yx'=yu'·ux',即y对x的导数等于y对u的导数与u对x的导数的乘积.
激趣诱思
知识点拨
名师点析求复合函数的导数需处理好以下环节:
(1)中间变量的选择应是基本函数结构;
(2)关键是正确分析函数的复合层次;
(3)一般是从最外层开始,由外及里,一层层地求导;
(4)善于把一部分表达式作为一个整体;
(5)最后要把中间变量换成关于自变量的函数.
激趣诱思
知识点拨
微思考
函数y=log2(x+1)是复合函数吗?是由哪些函数复合而成的?
提示:是,函数y=log2(x+1)是由y=log2u及u=x+1这两个函数复合而成的.
微练习
(1)函数y=sin 4x的导数为 ;?
(2)函数y= 的导数为 .?
探究一
探究二
探究三
素养形成
当堂检测
求复合函数的导数
例1求下列函数的导数:
(1)y=(4-3x)2;(2)y=cos(2x- );
(3)y=ln(4x-1);(4)y=e????2.
?
分析:先分析每个复合函数的构成,再按照复合函数的求导法则进行求导.
探究一
探究二
探究三
素养形成
当堂检测
解:(1)设y=u2,u=4-3x,则yu'=2u,ux'=-3,于是yx'=yu'·ux'=-6(4-3x)
=18x-24,即y'=18x-24.
(4)设y=eu,u=x2,则yu'=eu,ux'=2x,
于是yx'=yu'·ux'=e????2·2x,即y'=2xe????2.
?
探究一
探究二
探究三
素养形成
当堂检测
反思感悟1.解答此类问题常犯两个错误:
(1)不能正确区分所给函数是否为复合函数;
(2)若是复合函数,不能正确判断它是由哪些基本初等函数复合而成.
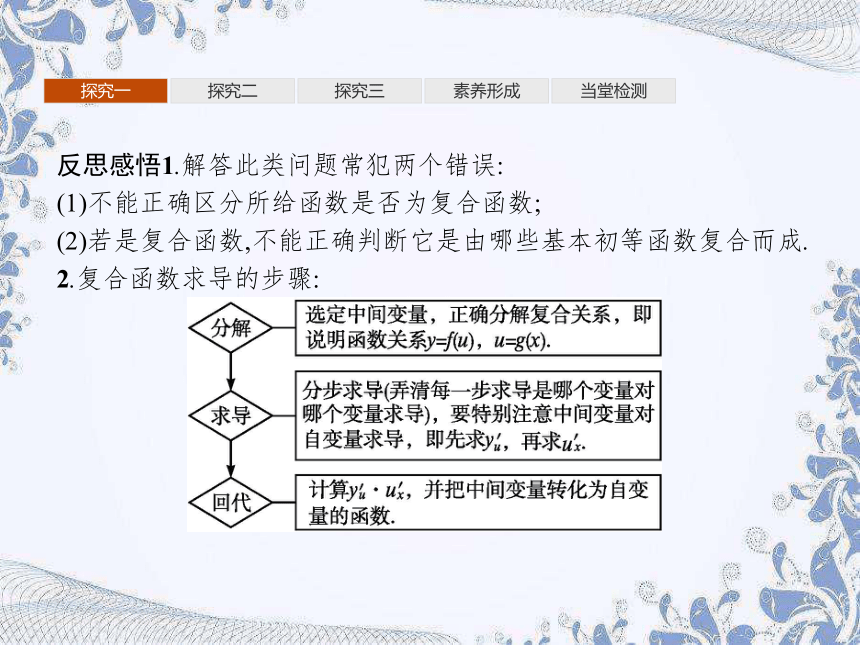
2.复合函数求导的步骤:
探究一
探究二
探究三
素养形成
当堂检测
变式训练1求下列函数的导数.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
复合函数求导与导数的运算法则的综合应用
例2求下列函数的导数.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟此类问题出错的主要因素一般有两个:一是基本初等函数的导数公式记忆有误;二是求导法则掌握不到位,尤其是对于积与商的求导法则中的符号问题出现混淆,导致运算结果出现错误.对于复杂函数求导,一般遵循先化简再求导的原则,但要注意化简过程中变换的等价性.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2求下列函数的导数:
(1)y=(2x-1)3;(2)y=sin 2x+cos 2x;(3)y=ln2x.
解:(1)设y=u3,u=2x-1,则yu'=3u2,ux'=2,于是yx'=yu'·ux'=6(2x-1)2,即y'=6(2x-1)2;
(2)y'=(sin 2x)'+(cos 2x)'=2cos 2x-2sin 2x;
探究一
探究二
探究三
素养形成
当堂检测
导数运算法则的综合应用
例3(1)曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是( )
(2)设曲线y=eax在点(0,1)处的切线与直线x+2y+1=0垂直,则a= .?
求P(x0,y0)→由点到直线的距离求最小值
(2)求y'→由y'|x=0=2求a的值
探究一
探究二
探究三
素养形成
当堂检测
解析:(1)设曲线y=ln(2x-1)在点(x0,y0)处的切线与直线2x-y+3=0平行.
(2)令y=f(x),则曲线y=eax在点(0,1)处的切线的斜率为f'(0),又切线与直线x+2y+1=0垂直,所以f'(0)=2.因为f(x)=eax,所以f'(x)=(eax)'=eax·(ax)'=aeax,所以f'(0)=ae0=a,故a=2.
答案:(1)A (2)2
探究一
探究二
探究三
素养形成
当堂检测
反思感悟导数综合应用的解题策略
本题正确地求出复合函数的导数是前提,审题时注意所给点是否是切点,挖掘题目隐含条件,求出参数,解决已知经过一定点的切线问题,寻求切点是解决问题的关键.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究1本例(1)的条件变为“曲线y=ln(2x-1)上的点到直线2x-y+m=0的最小距离为2 ”,求m的值.
即实数m的值为8或-12.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究2求本例(2)中曲线的切线与坐标轴围成的面积.
解:由题意可知,切线方程为y-1=2x,
即2x-y+1=0.
探究一
探究二
探究三
素养形成
当堂检测
等价转化思想在导数几何意义中的应用
典例已知点P是曲线y=f(x)=x2-ln x上任意一点,求点P到直线y=x-2的距离的最小值.
审题视角所求点P应为与直线y=x-2平行的曲线y=x2-ln x的切线的切点,此时最小距离应为该切线与已知直线之间的距离,即切点到已知直线的距离,从而转化为求曲线y=x2-ln x的斜率等于1的切线的切点坐标问题,故可借助导数的几何意义进行求解.
探究一
探究二
探究三
素养形成
当堂检测
解:由已知,可得当点P是曲线y=f(x)的平行于直线y=x-2的切线的切点时,点P到直线y=x-2的距离最小.
探究一
探究二
探究三
素养形成
当堂检测
方法点睛这类“求某曲线上任意一点到某已知直线的最小距离”问题,可结合图形,利用等价转化思想,将问题转化为求曲线的平行于已知直线的切线的切点问题,从而借助导数的几何意义进行求解.其基本步骤与方法如下:
(1)根据切线与已知直线平行,它们的斜率相等,得到切线的斜率.
(2)根据导数的几何意义,由切线的斜率得到切点的横坐标.
(3)由切点在曲线上,求得切点的纵坐标,得到切点的坐标.
(4)利用点到直线的距离公式求得最小距离.
探究一
探究二
探究三
素养形成
当堂检测
变式训练点P是曲线y=-x2上任意一点,则点P到直线y=x+2的最小距离为( )
解析:依题意知,点P就是曲线y=-x2上与直线y=x+2平行的切线的切点.设点P坐标为(x0,y0),因为y'=-2x,所以曲线在点P处的切线的斜率为k=-2x0.因为该切线与直线y=x+2平行,所以有-2x0=1,得
答案:B
探究一
探究二
探究三
素养形成
当堂检测
1.函数y=(x2-1)n的复合过程正确的是( )
A.y=un,u=x2-1
B.y=(u-1)n,u=x2
C.y=tn,t=(x2-1)n
D.y=(t-1)n,t=x2-1
答案:A
探究一
探究二
探究三
素养形成
当堂检测
2.(2020黑龙江大庆实验中学高二期末)已知f(x)=sin 2x+e2x,则f'(x)=( )
A.2cos 2x+2e2x
B.cos 2x+e2x
C.2sin 2x+2e2x
D.sin 2x+e2x
解析:因为f(x)=sin 2x+e2x,所以f'(x)=2cos 2x+2e2x.故选A.
答案:A
探究一
探究二
探究三
素养形成
当堂检测
3.(2020福建高二期末)已知f(x)=ln(2x+1)-ax,且f'(2)=-1,则a=( )
答案:A
探究一
探究二
探究三
素养形成
当堂检测
激趣诱思
知识点拨
我们学习过基本初等函数,如指数函数、对数函数、幂函数、三角函数、常数函数,我们可以把这些函数进行加、减、乘、除、乘方、开方等运算得到新的函数,还有一种构造新函数的方法,那就是把两个或几个函数“复合”起来,怎样“复合”呢,复合后的函数怎样求导呢?本节课就让我们来解决这些问题.
激趣诱思
知识点拨
1.复合函数的概念
一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).
2.复合函数的求导法则
一般地,对于由函数y=f(u)和u=g(x)复合而成的函数y=f(g(x)),它的导数与函数y=f(u),u=g(x)的导数间的关系为yx'=yu'·ux',即y对x的导数等于y对u的导数与u对x的导数的乘积.
激趣诱思
知识点拨
名师点析求复合函数的导数需处理好以下环节:
(1)中间变量的选择应是基本函数结构;
(2)关键是正确分析函数的复合层次;
(3)一般是从最外层开始,由外及里,一层层地求导;
(4)善于把一部分表达式作为一个整体;
(5)最后要把中间变量换成关于自变量的函数.
激趣诱思
知识点拨
微思考
函数y=log2(x+1)是复合函数吗?是由哪些函数复合而成的?
提示:是,函数y=log2(x+1)是由y=log2u及u=x+1这两个函数复合而成的.
微练习
(1)函数y=sin 4x的导数为 ;?
(2)函数y= 的导数为 .?
探究一
探究二
探究三
素养形成
当堂检测
求复合函数的导数
例1求下列函数的导数:
(1)y=(4-3x)2;(2)y=cos(2x- );
(3)y=ln(4x-1);(4)y=e????2.
?
分析:先分析每个复合函数的构成,再按照复合函数的求导法则进行求导.
探究一
探究二
探究三
素养形成
当堂检测
解:(1)设y=u2,u=4-3x,则yu'=2u,ux'=-3,于是yx'=yu'·ux'=-6(4-3x)
=18x-24,即y'=18x-24.
(4)设y=eu,u=x2,则yu'=eu,ux'=2x,
于是yx'=yu'·ux'=e????2·2x,即y'=2xe????2.
?
探究一
探究二
探究三
素养形成
当堂检测
反思感悟1.解答此类问题常犯两个错误:
(1)不能正确区分所给函数是否为复合函数;
(2)若是复合函数,不能正确判断它是由哪些基本初等函数复合而成.
2.复合函数求导的步骤:
探究一
探究二
探究三
素养形成
当堂检测
变式训练1求下列函数的导数.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
复合函数求导与导数的运算法则的综合应用
例2求下列函数的导数.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟此类问题出错的主要因素一般有两个:一是基本初等函数的导数公式记忆有误;二是求导法则掌握不到位,尤其是对于积与商的求导法则中的符号问题出现混淆,导致运算结果出现错误.对于复杂函数求导,一般遵循先化简再求导的原则,但要注意化简过程中变换的等价性.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2求下列函数的导数:
(1)y=(2x-1)3;(2)y=sin 2x+cos 2x;(3)y=ln2x.
解:(1)设y=u3,u=2x-1,则yu'=3u2,ux'=2,于是yx'=yu'·ux'=6(2x-1)2,即y'=6(2x-1)2;
(2)y'=(sin 2x)'+(cos 2x)'=2cos 2x-2sin 2x;
探究一
探究二
探究三
素养形成
当堂检测
导数运算法则的综合应用
例3(1)曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是( )
(2)设曲线y=eax在点(0,1)处的切线与直线x+2y+1=0垂直,则a= .?
求P(x0,y0)→由点到直线的距离求最小值
(2)求y'→由y'|x=0=2求a的值
探究一
探究二
探究三
素养形成
当堂检测
解析:(1)设曲线y=ln(2x-1)在点(x0,y0)处的切线与直线2x-y+3=0平行.
(2)令y=f(x),则曲线y=eax在点(0,1)处的切线的斜率为f'(0),又切线与直线x+2y+1=0垂直,所以f'(0)=2.因为f(x)=eax,所以f'(x)=(eax)'=eax·(ax)'=aeax,所以f'(0)=ae0=a,故a=2.
答案:(1)A (2)2
探究一
探究二
探究三
素养形成
当堂检测
反思感悟导数综合应用的解题策略
本题正确地求出复合函数的导数是前提,审题时注意所给点是否是切点,挖掘题目隐含条件,求出参数,解决已知经过一定点的切线问题,寻求切点是解决问题的关键.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究1本例(1)的条件变为“曲线y=ln(2x-1)上的点到直线2x-y+m=0的最小距离为2 ”,求m的值.
即实数m的值为8或-12.
探究一
探究二
探究三
素养形成
当堂检测
延伸探究2求本例(2)中曲线的切线与坐标轴围成的面积.
解:由题意可知,切线方程为y-1=2x,
即2x-y+1=0.
探究一
探究二
探究三
素养形成
当堂检测
等价转化思想在导数几何意义中的应用
典例已知点P是曲线y=f(x)=x2-ln x上任意一点,求点P到直线y=x-2的距离的最小值.
审题视角所求点P应为与直线y=x-2平行的曲线y=x2-ln x的切线的切点,此时最小距离应为该切线与已知直线之间的距离,即切点到已知直线的距离,从而转化为求曲线y=x2-ln x的斜率等于1的切线的切点坐标问题,故可借助导数的几何意义进行求解.
探究一
探究二
探究三
素养形成
当堂检测
解:由已知,可得当点P是曲线y=f(x)的平行于直线y=x-2的切线的切点时,点P到直线y=x-2的距离最小.
探究一
探究二
探究三
素养形成
当堂检测
方法点睛这类“求某曲线上任意一点到某已知直线的最小距离”问题,可结合图形,利用等价转化思想,将问题转化为求曲线的平行于已知直线的切线的切点问题,从而借助导数的几何意义进行求解.其基本步骤与方法如下:
(1)根据切线与已知直线平行,它们的斜率相等,得到切线的斜率.
(2)根据导数的几何意义,由切线的斜率得到切点的横坐标.
(3)由切点在曲线上,求得切点的纵坐标,得到切点的坐标.
(4)利用点到直线的距离公式求得最小距离.
探究一
探究二
探究三
素养形成
当堂检测
变式训练点P是曲线y=-x2上任意一点,则点P到直线y=x+2的最小距离为( )
解析:依题意知,点P就是曲线y=-x2上与直线y=x+2平行的切线的切点.设点P坐标为(x0,y0),因为y'=-2x,所以曲线在点P处的切线的斜率为k=-2x0.因为该切线与直线y=x+2平行,所以有-2x0=1,得
答案:B
探究一
探究二
探究三
素养形成
当堂检测
1.函数y=(x2-1)n的复合过程正确的是( )
A.y=un,u=x2-1
B.y=(u-1)n,u=x2
C.y=tn,t=(x2-1)n
D.y=(t-1)n,t=x2-1
答案:A
探究一
探究二
探究三
素养形成
当堂检测
2.(2020黑龙江大庆实验中学高二期末)已知f(x)=sin 2x+e2x,则f'(x)=( )
A.2cos 2x+2e2x
B.cos 2x+e2x
C.2sin 2x+2e2x
D.sin 2x+e2x
解析:因为f(x)=sin 2x+e2x,所以f'(x)=2cos 2x+2e2x.故选A.
答案:A
探究一
探究二
探究三
素养形成
当堂检测
3.(2020福建高二期末)已知f(x)=ln(2x+1)-ax,且f'(2)=-1,则a=( )
答案:A
探究一
探究二
探究三
素养形成
当堂检测
