直线、射线、线段 说课稿
图片预览







文档简介
(共35张PPT)
教学背景分析
1
教学目标分析
2
教法和学法分析
3
教学程序设计
4
关于教学内容和要求的分析
学生情况
分 析
一、教学背景分析
“直线、射线、线段” 是新人教版《七年级数学》上册第四章第二节内容。 在小学阶段,学生主要通过实例初步了解直线、射线、线段的图形特征,能区分直线、射线、线段的概念并体会它们的一些性质,本节课将进一步认识直线、射线、线段和角,理解它们的概念,了解有关的一些性质,并能初步应用。
直线、射线、线段是最简单的几何图形,是研究三角形、四边形等比较复杂图形的必要基础。从本节课开始出现的几何图形的表示法、几何语言的表达方式,也是今后系统学习几何知识所必须的基础。因此,本节课在学生今后的整个几何学习中,起着奠基的作用。
依据教材的内容与要求,以及学生的认知水平,本节课将安排2-3个课时完成教学任务。
一、教学背景分析
理解两点确定一条直线的事实;掌握直线、射线、线段表示方法;理解直线、射线、线段的联系与区别.
观察图片感性认识几何图形,在实际背景中理解图形的概念和性质,经历探索图形性质的过程;通过对学生进行几何语言和识图能力的训练,培养学生三种语言的转化能力。
让学生体验数学来源于生活,认识到现实生活中蕴含着大量的数学事实,激发学生的好奇心和求知欲.
教学目标设计
知识与技能
过程与方法
情感态度与价值观
二、教学目标分析
难点
图形语言、符号语言、文字语言的相互转化.
二、教学目标分析
重点
认识直线、射线、线段的区别与联系. 正确表示直线、射线、线段,逐步使学 生懂得几何语句的意义及直线的基本性质.
教学方法:直观演示、阅读理解与尝试指导相结合.
教学用具: 多媒体课件及画图的工具
学习方法:以直观形象来理解概念,以动手操作体会画法及性质.
三、教法学法分析
创设情景,引出课题
探索实践,自主归纳
巩固新知,应用新知
回顾反思,升华提高
四、教法程序设计
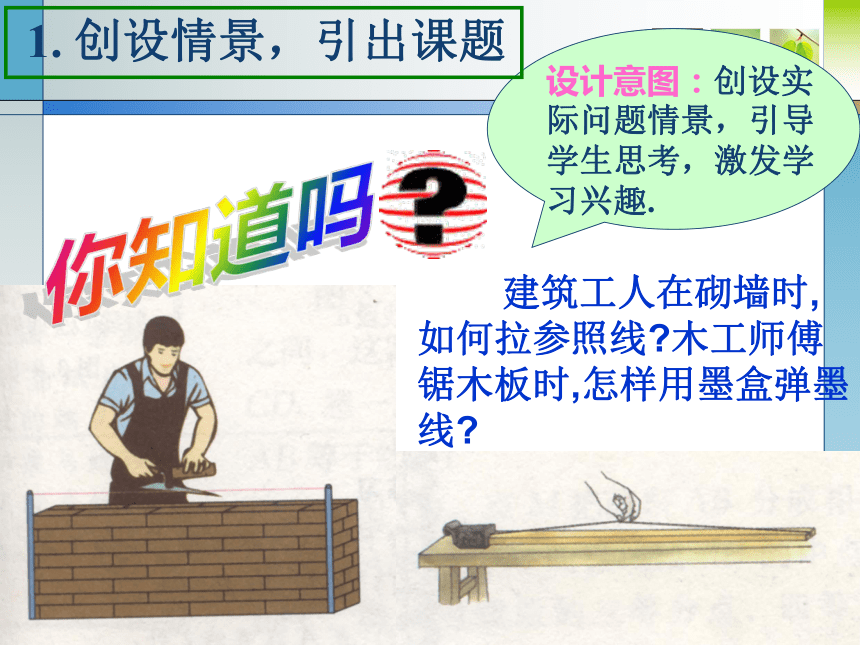
设计意图:创设实际问题情景,引导学生思考,激发学习兴趣.
建筑工人在砌墙时, 如何拉参照线 木工师傅锯木板时,怎样用墨盒弹墨线
1. 创设情景,引出课题
生活中有哪些物体可以近似地看成线段、射线、直线?
设计意图:通过观察抽象出直线、射线、线段的几何形象,让学生体验图形是描述现实世界的重要手段.
2.探索实践,自主归纳
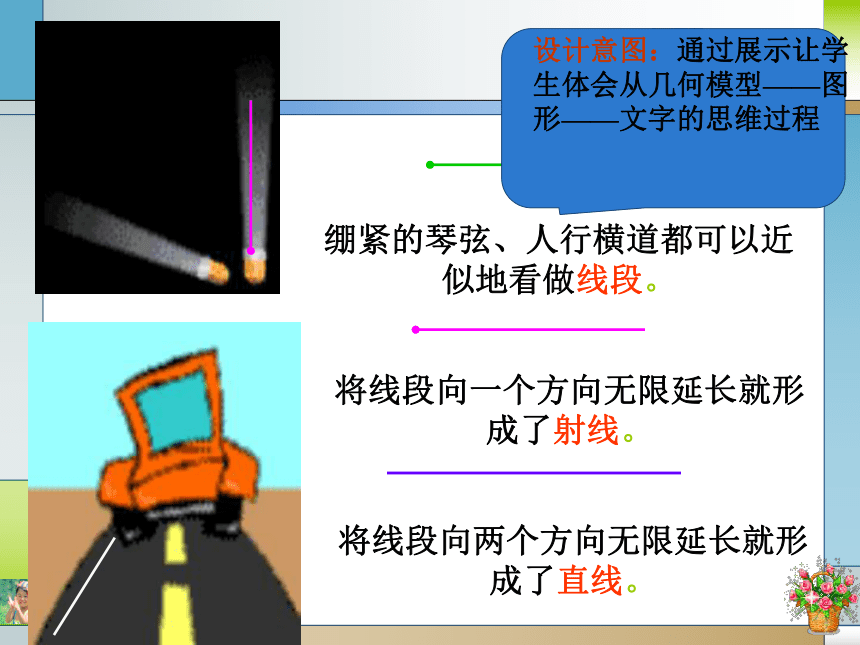
绷紧的琴弦、人行横道都可以近似地看做线段。
将线段向一个方向无限延长就形成了射线。
将线段向两个方向无限延长就形成了直线。
设计意图:通过展示让学生体会从几何模型——图形——文字的思维过程
直线、射线、线段有什么区别与联系
议 一 议
类型 端点个数 延伸性 能否度量
线段
射线
直线
设计意图:通过对直线、射线、线段的联系和区别的探究,进一步发展学生抽象概括的能力.
注意问题:(1)线段、直线表示与字母顺序无关
(2)射线表示有方向性,端点在前,射线上任意一点在后
A
B
表示:直线 AB(或直线BA)
表示:直线
A
B
表示:线段 AB(或线段BA)
表示:射线 OA
表示:线段 a
a
表示:射线
O
A
设计意图:在明确直线、射线、线段区别的基础上,讲授它们的表示方法,有助于学生的理解和掌握.体会从文字叙述——符号表示的转变。
怎样用数学符号表示直线、射线、线段?
A
B
线段AB与线段BA是同一条线段吗?
直线AB与直线BA是同一条直线吗?
射线AB与射线BA是同一条射线吗?
1、如果你想将一根细木条固定在墙上,至少需要几个钉子?
探究活动一
设计意图:观察思考生活中的问题,引导学生从感性的认识到理性思考的提升,学会从几何模型抽象为几何图形,养成探究的习惯。
设计意图:让学生通过动手实践,观察分析,猜想,体验并感悟到直线的性质.引导学生自己归纳性质,并在交流中完善表述.培养归纳和语言表达能力。
(1)过一点可以画几条直线?
(2)过两点可以画几条直线?
经过两点有且只有一条直线
两点确定一条直线。
1、建筑工人在砌墙时经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线, 根据什么道理?
设计意图:解决问题,学以致用
两点确定一条直线的应用:
2、建筑工人在砌墙时,这样拉出的参照线就是直的(如图所示);木工师傅用墨盒弹出的墨线也是直的,你能用刚才学过的几何知识解释来他们这样做的道理吗?
3、植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
4、射击的时候,你知道是如何瞄准目标的吗?
判断:
1、射线是直线的一部分。 ( )
2、线段是射线的一部分。 ( )
3、画一条射线,使它的长度为3cm。 ( )
4、线段AB和线段BA是同一条线段。 ( )
5、射线OP和射线PO是同一条射线。 ( )
6、如图,画一条线段ab。 ( )
a
b
√
√
√
×
×
×
3.巩固新知,应用新知
设计意图:通过本题巩固学生对概念和表示法的理解。
例1、已知平面上四个点A、B、C、D
读下列语句,并画出相应的图形
①画直线AB
②画线段AC
③画射线AD、DC、CB
设计意图:本例题主要强化学生学会从文字语言和符号语言向图形语言的转化,并为下面的练习解答做示范和铺垫。
(1)直线EF经过点C
E
F
C
随堂练习一
(2)经过点O的三条线段a、b、c
(3)线段AB、CD相交于点B
设计意图:课本练习同步训练,及时验收。
1. 按下列语句画出图形.
(2)经过点O的三条线段a、b、c
o
b
c
a
随堂练习一
B
D
A
C
(3)线段AB、CD相交于点B
随堂练习一
l
A
点A在直线 l 上
2、看图说话
随堂练习一
点A在直线 l 外
l
A
点与直线的位置关系:
1.一个点在一条直线上,也可以说这条直线经过这个点.
2.一个点在一条直线外,也可以说这条直线不经过这个点.
随堂练习一
2、看图说话
O
a
b
直线a和直线b相交于点O
当两条不同的直线有一个公共点时,我们就称两条直线相交,这个公共点叫做它们的交点.
A
B
E
C
D
解:有10条线段分别是AB、AC、AD、AE、BC、BD、BE、CD、CE、DE.
例2.指出下图中线段、射线、直线分别有多少条?并表示出来.
有8条射线
只有1条直线,是直线BC
设计意图:设计以复杂的图形为背景的例题,让学生体会从复杂图形找出基本图形的过程,学会分类解决问题,学会从简单入手解决较复杂的问题,为今后的学习做铺垫。
1.经过A、B、C三个点中的任意两点可以画几条直线?
2.两条直线相交,有一个交点,三条直线相交有几个交点?最多有几个?
设计意图:本练习延续前面的问题探究,根据学生的实际情况可以穿插于课堂教学中,又可作为课后拓展练习用。旨在引导学生学会深入探究问题,发展学生思维的广阔性和深刻性。
拓展练习
答:10种
3.往返A、E两地的汽车,中途需要停靠B 、C 、D三个站点,根据你所学的知识回答: 需要制定多少种不同的票价?
A B C D E
拓展练习
数学问题
实际问题
转 化 为
回顾一下,我想说…
直线、射线、线段的联系与区别.
直线 、射线 、线段的表示方法.
两点确定一条直线.
分类思想,转化思想,有序思考。
数学知识:
数学思想及方法:
课堂小结
不同几何语言(文字语言、符号语言、图形语言)的相互转化。
拓展与创新题:
(1)教科书P134 习题4.2第11题.
必做题:
教科书P132 习题4.2第2、3、4题.
(2)过同一平面上的三点中其中的任两个点,可以画几条直线 四点呢?你能发现什么规律。
布置作业
板书设计:
4.2直线、射线、线段
A
B
表示:线段 AB(或线段BA)
a
表示:线段 a
表示:直线 AB(或直线BA)
A
B
l
表示:直线 l
表示:射线 OA
A
O
一、直线、射线、线段的表示方法:
二、直线公理:经过两点有且只有一条直线。
多媒体
学生练习位置
教学建议:
1.通读教材、理解教材,依据教学内容和要求以及学生的学情对教材进行合理的处理整合是备课的关键环节。
2.注意与小学相关内容的衔接。创设问题情境,目的在于激发学生思考,回顾旧知。教学的开始从观赏生活中的图片入手,引导学生经历感性到理性思维的转变,引出新知。力求自然有效。
3.作为几何的入门教学,教师应注重概念间的联系,在对比中加深理解。强化几何模型——图形——文字——符号的互相转化。
教学背景分析
1
教学目标分析
2
教法和学法分析
3
教学程序设计
4
关于教学内容和要求的分析
学生情况
分 析
一、教学背景分析
“直线、射线、线段” 是新人教版《七年级数学》上册第四章第二节内容。 在小学阶段,学生主要通过实例初步了解直线、射线、线段的图形特征,能区分直线、射线、线段的概念并体会它们的一些性质,本节课将进一步认识直线、射线、线段和角,理解它们的概念,了解有关的一些性质,并能初步应用。
直线、射线、线段是最简单的几何图形,是研究三角形、四边形等比较复杂图形的必要基础。从本节课开始出现的几何图形的表示法、几何语言的表达方式,也是今后系统学习几何知识所必须的基础。因此,本节课在学生今后的整个几何学习中,起着奠基的作用。
依据教材的内容与要求,以及学生的认知水平,本节课将安排2-3个课时完成教学任务。
一、教学背景分析
理解两点确定一条直线的事实;掌握直线、射线、线段表示方法;理解直线、射线、线段的联系与区别.
观察图片感性认识几何图形,在实际背景中理解图形的概念和性质,经历探索图形性质的过程;通过对学生进行几何语言和识图能力的训练,培养学生三种语言的转化能力。
让学生体验数学来源于生活,认识到现实生活中蕴含着大量的数学事实,激发学生的好奇心和求知欲.
教学目标设计
知识与技能
过程与方法
情感态度与价值观
二、教学目标分析
难点
图形语言、符号语言、文字语言的相互转化.
二、教学目标分析
重点
认识直线、射线、线段的区别与联系. 正确表示直线、射线、线段,逐步使学 生懂得几何语句的意义及直线的基本性质.
教学方法:直观演示、阅读理解与尝试指导相结合.
教学用具: 多媒体课件及画图的工具
学习方法:以直观形象来理解概念,以动手操作体会画法及性质.
三、教法学法分析
创设情景,引出课题
探索实践,自主归纳
巩固新知,应用新知
回顾反思,升华提高
四、教法程序设计
设计意图:创设实际问题情景,引导学生思考,激发学习兴趣.
建筑工人在砌墙时, 如何拉参照线 木工师傅锯木板时,怎样用墨盒弹墨线
1. 创设情景,引出课题
生活中有哪些物体可以近似地看成线段、射线、直线?
设计意图:通过观察抽象出直线、射线、线段的几何形象,让学生体验图形是描述现实世界的重要手段.
2.探索实践,自主归纳
绷紧的琴弦、人行横道都可以近似地看做线段。
将线段向一个方向无限延长就形成了射线。
将线段向两个方向无限延长就形成了直线。
设计意图:通过展示让学生体会从几何模型——图形——文字的思维过程
直线、射线、线段有什么区别与联系
议 一 议
类型 端点个数 延伸性 能否度量
线段
射线
直线
设计意图:通过对直线、射线、线段的联系和区别的探究,进一步发展学生抽象概括的能力.
注意问题:(1)线段、直线表示与字母顺序无关
(2)射线表示有方向性,端点在前,射线上任意一点在后
A
B
表示:直线 AB(或直线BA)
表示:直线
A
B
表示:线段 AB(或线段BA)
表示:射线 OA
表示:线段 a
a
表示:射线
O
A
设计意图:在明确直线、射线、线段区别的基础上,讲授它们的表示方法,有助于学生的理解和掌握.体会从文字叙述——符号表示的转变。
怎样用数学符号表示直线、射线、线段?
A
B
线段AB与线段BA是同一条线段吗?
直线AB与直线BA是同一条直线吗?
射线AB与射线BA是同一条射线吗?
1、如果你想将一根细木条固定在墙上,至少需要几个钉子?
探究活动一
设计意图:观察思考生活中的问题,引导学生从感性的认识到理性思考的提升,学会从几何模型抽象为几何图形,养成探究的习惯。
设计意图:让学生通过动手实践,观察分析,猜想,体验并感悟到直线的性质.引导学生自己归纳性质,并在交流中完善表述.培养归纳和语言表达能力。
(1)过一点可以画几条直线?
(2)过两点可以画几条直线?
经过两点有且只有一条直线
两点确定一条直线。
1、建筑工人在砌墙时经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线, 根据什么道理?
设计意图:解决问题,学以致用
两点确定一条直线的应用:
2、建筑工人在砌墙时,这样拉出的参照线就是直的(如图所示);木工师傅用墨盒弹出的墨线也是直的,你能用刚才学过的几何知识解释来他们这样做的道理吗?
3、植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
4、射击的时候,你知道是如何瞄准目标的吗?
判断:
1、射线是直线的一部分。 ( )
2、线段是射线的一部分。 ( )
3、画一条射线,使它的长度为3cm。 ( )
4、线段AB和线段BA是同一条线段。 ( )
5、射线OP和射线PO是同一条射线。 ( )
6、如图,画一条线段ab。 ( )
a
b
√
√
√
×
×
×
3.巩固新知,应用新知
设计意图:通过本题巩固学生对概念和表示法的理解。
例1、已知平面上四个点A、B、C、D
读下列语句,并画出相应的图形
①画直线AB
②画线段AC
③画射线AD、DC、CB
设计意图:本例题主要强化学生学会从文字语言和符号语言向图形语言的转化,并为下面的练习解答做示范和铺垫。
(1)直线EF经过点C
E
F
C
随堂练习一
(2)经过点O的三条线段a、b、c
(3)线段AB、CD相交于点B
设计意图:课本练习同步训练,及时验收。
1. 按下列语句画出图形.
(2)经过点O的三条线段a、b、c
o
b
c
a
随堂练习一
B
D
A
C
(3)线段AB、CD相交于点B
随堂练习一
l
A
点A在直线 l 上
2、看图说话
随堂练习一
点A在直线 l 外
l
A
点与直线的位置关系:
1.一个点在一条直线上,也可以说这条直线经过这个点.
2.一个点在一条直线外,也可以说这条直线不经过这个点.
随堂练习一
2、看图说话
O
a
b
直线a和直线b相交于点O
当两条不同的直线有一个公共点时,我们就称两条直线相交,这个公共点叫做它们的交点.
A
B
E
C
D
解:有10条线段分别是AB、AC、AD、AE、BC、BD、BE、CD、CE、DE.
例2.指出下图中线段、射线、直线分别有多少条?并表示出来.
有8条射线
只有1条直线,是直线BC
设计意图:设计以复杂的图形为背景的例题,让学生体会从复杂图形找出基本图形的过程,学会分类解决问题,学会从简单入手解决较复杂的问题,为今后的学习做铺垫。
1.经过A、B、C三个点中的任意两点可以画几条直线?
2.两条直线相交,有一个交点,三条直线相交有几个交点?最多有几个?
设计意图:本练习延续前面的问题探究,根据学生的实际情况可以穿插于课堂教学中,又可作为课后拓展练习用。旨在引导学生学会深入探究问题,发展学生思维的广阔性和深刻性。
拓展练习
答:10种
3.往返A、E两地的汽车,中途需要停靠B 、C 、D三个站点,根据你所学的知识回答: 需要制定多少种不同的票价?
A B C D E
拓展练习
数学问题
实际问题
转 化 为
回顾一下,我想说…
直线、射线、线段的联系与区别.
直线 、射线 、线段的表示方法.
两点确定一条直线.
分类思想,转化思想,有序思考。
数学知识:
数学思想及方法:
课堂小结
不同几何语言(文字语言、符号语言、图形语言)的相互转化。
拓展与创新题:
(1)教科书P134 习题4.2第11题.
必做题:
教科书P132 习题4.2第2、3、4题.
(2)过同一平面上的三点中其中的任两个点,可以画几条直线 四点呢?你能发现什么规律。
布置作业
板书设计:
4.2直线、射线、线段
A
B
表示:线段 AB(或线段BA)
a
表示:线段 a
表示:直线 AB(或直线BA)
A
B
l
表示:直线 l
表示:射线 OA
A
O
一、直线、射线、线段的表示方法:
二、直线公理:经过两点有且只有一条直线。
多媒体
学生练习位置
教学建议:
1.通读教材、理解教材,依据教学内容和要求以及学生的学情对教材进行合理的处理整合是备课的关键环节。
2.注意与小学相关内容的衔接。创设问题情境,目的在于激发学生思考,回顾旧知。教学的开始从观赏生活中的图片入手,引导学生经历感性到理性思维的转变,引出新知。力求自然有效。
3.作为几何的入门教学,教师应注重概念间的联系,在对比中加深理解。强化几何模型——图形——文字——符号的互相转化。
