【2020年暑期衔接】青岛版八下 第18讲 一次函数与一元一次不等式(含解析)
文档属性
| 名称 | 【2020年暑期衔接】青岛版八下 第18讲 一次函数与一元一次不等式(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 586.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020年暑期衔接训练青岛版数学八年级下册:第18讲
一次函数
与一元一次不等式
一、单选题:
1.已知函数
,当
时,y的取值范围是(????
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
2.如图,函数
和
的图象相交于点
,则关于x的不等式
的解集是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为(??
)
A.?x≤3????????????????????????????????????B.?x≥3????????????????????????????????????C.?x≤
????????????????????????????????????D.?x≥
4.某便利店的咖啡单价为10元/杯,为了吸引顾客,该店共推出了三种会员卡,如下表:
会员卡类型
办卡费用/元
有效期
优惠方式
A类
40
1年
每杯打九折
B类
80
1年
每杯打八折
C类
130
1年
一次性购买2杯,第二杯半价
例如,购买A类会员卡,1年内购买50次咖啡,每次购买2杯,则消费
元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为(???
)
A.?购买A类会员卡????????????B.?购买B类会员卡?????????????C.?购买C类会员卡????????????D.?不购买会员卡
5.如图,一次函数
的图象经过点
,则关于
的不等式
的解集为(???
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
6.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是(???
)
A.?0???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
7.如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为0,AB⊥x轴于点B,△AOB的面积为3,则满足y1)
A.?x>2??????????????????????????????????????B.?x<2??????????????????????????????????????C.?x>3??????????????????????????????????????D.?x<3
8.如图,已知直线
过点
,过点
的直线
交
轴于点
,则关于的不等式组
的解集为(???
)
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
9.如图,函数
和
的图象相交于点
,则关于
的不等式
的解集为(??
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
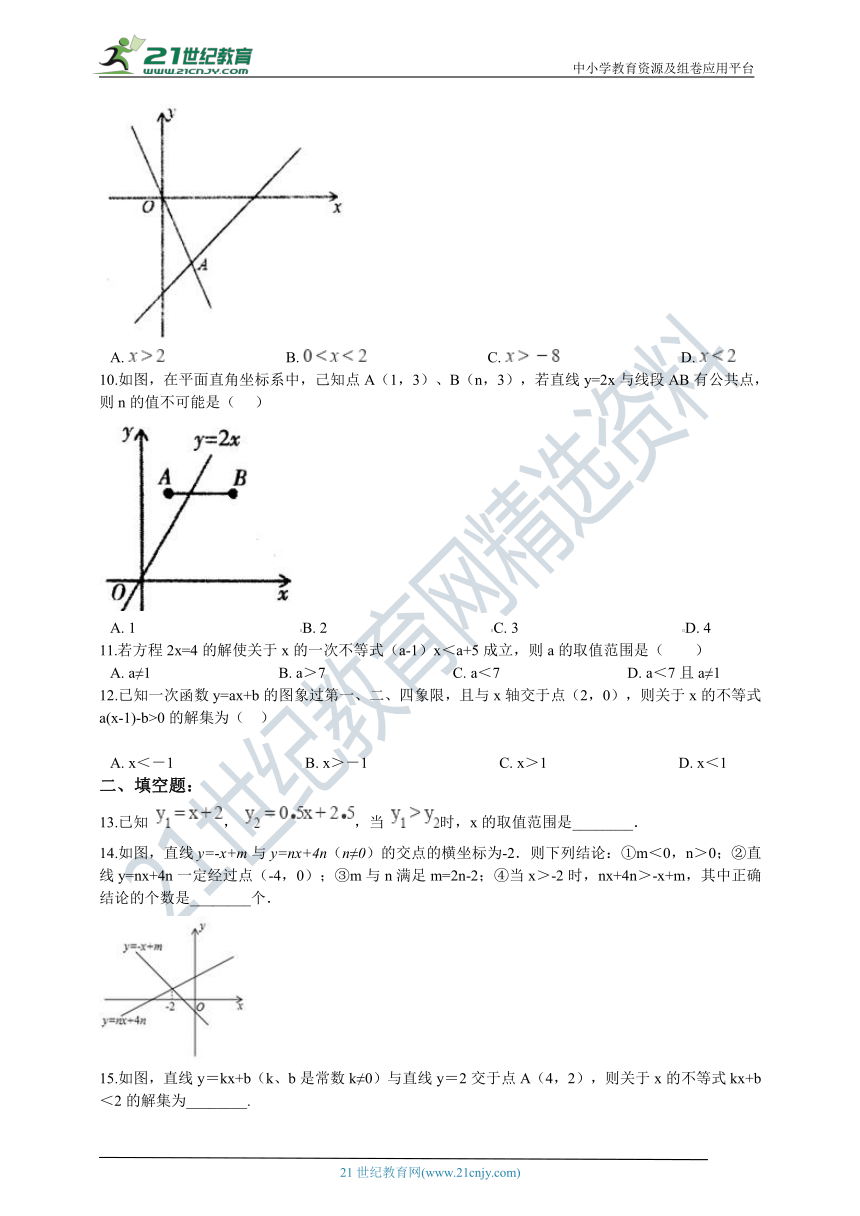
10.如图,在平面直角坐标系中,己知点A(1,3)、B(n,3),若直线y=2x与线段AB有公共点,则n的值不可能是(???
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
11.若方程2x=4的解使关于x的一次不等式(a-1)x<a+5成立,则a的取值范围是( )
A.?a≠1?????????????????????????????????B.?a>7?????????????????????????????????C.?a<7?????????????????????????????????D.?a<7且a≠1
12.已知一次函数y=ax+b的图象过第一、二、四象限,且与x轴交于点(2,0),则关于x的不等式a(x-1)-b>0的解集为(??
)
A.?x<-1??????????????????????????????????B.?x>-1??????????????????????????????????C.?x>1??????????????????????????????????D.?x<1
二、填空题:
13.已知
,
,当
时,x的取值范围是________.
14.如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2.则下列结论:①m<0,n>0;②直线y=nx+4n一定经过点(-4,0);③m与n满足m=2n-2;④当x>-2时,nx+4n>-x+m,其中正确结论的个数是________个.
15.如图,直线y=kx+b(k、b是常数k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为________.
16.直线y=kx和y=ax+4交于A(1,k),则不等式kx-617.如图,一次函数
与y=kx+b(k、b为常数,且k≠0)的图像相交于点A(m,-2),则m=________,关于x的不等式组
?的解是________。
18.一次函数y=kx+b的图象经过A(-1,1)和B(-
?,0),则不等式组
的解为________.
19.若直线y=kx+k+1经过点(m
,
n+2)和(m+1,2n﹣1),且0<k<2,n是整数,则n=________.
20.如图,直线
过点A(0,2),且与直线
交于点P(1,m),则不等式组
>
>
-2的解集是________
?
三、解答题:
21.已知x2+ax+3=(x﹣1)(x﹣b),试求直线y=2x﹣a与直线y=bx+3的交点坐标,并直接写出关于x的不等式2x﹣a≥bx+3的解集.
22.如图是一次函数y=2x﹣5的图象,请根据给出的图象写出一个一元一次方程和一个一元一次不等式,并用图象求解所写出的方程和不等式.
23.已知函数y=ax+b,y随x增大而减少,且交x轴于A(3,0),求不等式(a﹣b)x﹣2b<0的解集.
24.学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2
,
且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)当参加老师的人数为多少人时,选择甲旅行社合算?
(3)如果全共有50人参加时,选择哪家旅行社合算?
25.如图,直线l是一次函数y=kx+b的图象,点A、B在直线l上,根据图象回答下列问题:
(1)写出方程kx+b=0的解;
(2)写出不等式kx+b>2的解集;
(3)若直线l上的点P(m
,
n)在线段AB上移动,则m、n的取值范围分别是什么?
26.已知一次函数y1=﹣2x﹣3与y2=x+2.
(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3>x+2的解集为多少?
(3)求两图象和y轴围成的三角形的面积.
27.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1
、y2
(km),
y1
、y2
与x的函数关系如图所示.
(1)填空:A、C两港口间的距离为________km,
________;
(2)求图中点P的坐标;
(3)若两船的距离不超过8km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
答案解析部分
一、单选题
1.【答案】
C
解:
,因为k<0,所以y随x的增大而减小.
当x=-1时,y=
;当x=1时,y=
.
所以当
时,y的取值范围是
.
故答案为:C.
【分析】由k=<0可知y随x的增大而减小,据此由x的取值范围即可得y的取值范围。
2.【答案】
A
解:
函数
和
的图象相交于点
,
不等式
的解集为
.
故选A
.
【分析】以交点为分界,结合图象写出不等式mx>x+3的解集即可.
3.【答案】D
解:∵函数y=2x的图象过点A(m,3),
∴将点A(m,3)代入y=2x得,2m=3,
解得,m=
,
∴点A的坐标为(
,3),
∴由图可知,不等式2x≥ax+4的解集为x≥
.
故选:D.
【分析】首先利用待定系数法求出A点坐标,再以交点为分界,结合图象写出不等式2x≥ax+4的解集即可.
4.【答案】
C
解:设一年内在该便利店买咖啡的次数为x次,消费的钱数为y元,根据题意得:yA=40+0.9
x=40+18x,yB=80+0.8
x=80+16x,yC=130+15
=130+15x,
当75≤x≤85时,
1390≤yA≤1570;
1280≤yB≤1440;
1255≤yC≤1405;
由此可见,C类会员年卡消费最低,所以最省钱的方式为购买C类会员年卡.
故答案为:C.
【分析】设一年内在该便利店买咖啡的次数为x次,消费的钱数为y元,根据题意得:列出3类会员卡用含x的关系表示消费的费用y,再确定y的范围,进行比较即可解答.
5.【答案】
A
解:∵
,
,
∴kx+b<-3即y<-3,
∵一次函数
的图象经过点B(4,-3),
∴当x=4时y=-3,
由图象得y随x的增大而减小,当
时,y<-3,
故答案为:A.
【分析】由
即y<-3,根据图象即可得到答案.
6.【答案】
B
解:∵y1=kx+b的函数值随x的增大而减小,
∴k<0;故①符合题意
∵y2=x+a的图象与y轴交于负半轴,
∴a<0;
当x<3时,相应的x的值,y1图象均高于y2的图象,
∴y1>y2
,
故②③不符合题意.
故答案为:B.
【分析】根据y1=kx+b和y2=x+a的图象可知:k<0,a<0,当x<3时,y1>y2
,
可得出①符合题意,②③不符合题意,即可求解.
7.【答案】
B
解:因为△AOB的面积为3,函数y1=kx(k>0)和y2=ax+4(a<0)
的图象相交于点4(m,3),
可得:
·3m=3,解得:m=2,
所以满足y1故答案为:B。
【分析】利用点A的坐标和△AOB的面积为3,建立关于m的方程,解方程求出m的值,可得到点A的坐标,然后观察函数图像可求出满足y18.【答案】
D
解:过点A作AC
y轴,交x轴于点C,
∵
,
∴C(-2,0),
根据图象可知:直线AC与y轴之间的函数图像上的点所对应的x的取值范围(包含-2,不包含0)就是关于x的不等式组
的解集,
∴不等式组
的解集是:
.
故答案为:D.
【分析】根据关于x的不等式组
的解集与一次函数图象之间的关系,即可得到答案.
9.【答案】
A
解:∵函数y=?4x和y=kx+b的图象相交于点A(m,?8),
∴?8=?4m,
解得:m=2,
故A点坐标为(2,?8),
∵kx+b>?4x时,(k+4)x+b>0,
则关于x的不等式(k+4)x+b>0的解集为:x>2.
故答案为:A.
【分析】直接利用函数图象上点的坐标特征得出m的值,再利用函数图象得出答案即可.
10.【答案】
A
解:∵直线y=2x与线段AB有公共点
∴2n≥3
解得
n≥
∵1<
∴n的值不可能是1.
故答案为:A.
【分析】当直线y=2x与线段AB有公共点时,直线y=2x的图象不能在直线y=3下方,据此列出不等式求出n的取值范围即可判断出结论。
11.【答案】
D
解:
解方程2x=4得:x=2,
∵(a-1)x<a+5,
当a-1>0时,x<
,
∴
>2,
∴1<a<7.
当a-1<0时,x>
∴
<2,
∴a<1.
则a的取值范围是a<7且a≠1.
故答案为:D
【分析】先求出方程2x=4的解,再根据不等式(a-1)x<a+5用a表示出x的取值范围,即可求出a的取值范围
12.【答案】
A
解:依题意作图,
可知直线从左往右下降,则a<0。直线交y轴于上半轴,说明b>0。把点(2,0)代入原式解得b=-2a.
所以代入a(x-1)-b>0得a(x-1)+2a>0.
解得a(x+1)>0。所以x+1<0.则不等式的解集为x<-1.
选A.
【点评】本题难度中等。作图辅助判断出a,b值的范围为解题关键。做这类题要注意数形结合的思想。
二、填空题
13.【答案】
解:因为
,既可以转化为不等式
经过解得不等式可以得到
故答案为:
【分析】把
,
,代入
,解不等式即可.
14.【答案】
4
解:①∵直线y=?x+m与y轴交于负半轴,∴m<0;
∵y=nx+4n(n≠0)的图象从左往右逐渐上升,∴n>0,
故结论①正确;
②将x=?4代入y=nx+4n,得y=?4n+4n=0,
∴直线y=nx+4n一定经过点(?4,0).
故结论②正确;
③∵直线y=?x+m与y=nx+4n(n≠0)的交点的横坐标为?2,
∴当x=?2时,y=2+m=?2n+4n,
∴m=2n?2.
故结论③正确;
④∵当x>?2时,直线y=nx+4n在直线y=?x+m的上方,
∴当x>?2时,nx+4n>?x+m,
故结论④正确.
故答案为:4.
【分析】①由直线y=?x+m与y轴交于负半轴,可得m<0;y=nx+4n(n≠0)的图象从左往右逐渐上升,可得n>0,即可判断结论①正确;②将x=?4代入y=nx+4n,求出y=0,即可判断结论②正确;③代入交点坐标整理即可判断结论③正确;④观察函数图象,可知当x>?2时,直线y=nx+4n在直线y=?x+m的上方,即nx+4n>?x+m,即可判断结论④正确.
15.【答案】
x<4
解:∵直线y=kx+b与直线y=2交于点A(4,2),
∴x<4时,y<2,
∴关于x的不等式kx+b<2的解集为x<4.
故答案为
:x<4.
【分析】观察函数图象,写出直线y=kx+2在直线y=2下方所对应的自变量的范围即可.
16.【答案】
1解:∵直线y=kx和y=ax+4交于A(1,k),
∴a+4=k
∴a=k-4,
kx-6<(k-4)x+4
∴kx-6<(k-4)x+4
解之:x,
由图像可知当x>1时,kx>ax+4,
∴当1<x<2.5时,kx-6故答案为:1<x<2.5.
【分析】由题意可知将点A的坐标代入y=ax+4,可得到a=k-4,再由kx-617.【答案】
-3;
-解:∵-2=-m-6,
解得m=-3,
则由图象可得当x<-3时,kx+b<-x-6,
当-x-6=0,
解得x=-,
由图象可得当x>-时,y=-x-6<0,
综上不等式组的解集为:-故答案为:-3,-【分析】把y=-2代入y=-x-6中,即可求出m的值;于是看图象即可得出当x<-3时,y=kx+b图象在y=-x-6图象的下面,
即kx+b<-x-6,
令y=-x-6=0,
求出其与x轴的交点,可得x>-时,y=-x-6的图象在x轴下方,即y<0,
两者结合即可得出不等式组的解集.
18.【答案】
-
<x<-1
解:由题意可得:一次函数图象在y=1的下方时x<-1,在y=0的上方时x>-
,
∴关于x的不等式0<kx+b<1的解集是-
<x<-1.
故答案为:-
<x<-1.
【分析】首先利用图象可找到图象在y=1的下方时,x<-1,在y=0的上方时x>-,
进而得到关于x的不等式0<x<1。
19.【答案】
4
解:依题意得:
,
∴k=n﹣3,
∵0<k<2,
∴0<n﹣3<2,
∴3<n<5,
∵n是整数,则n=4
故答案为4.
【分析】将两点代入直线解析式,解出n的取值范围,得出n的取值。
20.【答案】
1<x<2
解:由于直线
过点A(0,2),P(1,m),
则
,解得
,
,
故所求不等式组可化为:
mx>(m-2)x+2>mx-2,
0>-2x+2>-2,
解得:1<x<2,
【分析】根据待定系数法,用含m的代数式表示函数,
根据题意,列出关于x的不等式组,进而求解.
三、解答题
21.
解:∵x2+ax+3=(x﹣1)(x﹣b)=x2﹣(b+1)x+b,
∴b=3,a=﹣(b+1)=﹣4.
联立两函数解析式成方程组,
,解得:
,
∴直线y=2x+4与直线y=3x+3的交点坐标为(1,6).
画出两直线,如图所示,
观察函数图象可知,当x<1时,直线y=2x+4在直线y=3x+3的上方,
∴不等式2x+4≥3x+3的解集为x≤1.
【分析】根据给定等式可求出a、b的值,联立两函数解析式成方程组,通过解方程组可求出两直线的交点坐标,画出两直线,根据直线的上下位置关系,即可得出不等式2x+4≥3x+3的解集.
22.解:根据给出的图象可写出一个一元一次方程为2x﹣5=0,一个一元一次不等式为2x﹣5>0.
∵一次函数y=2x﹣5的图象与x轴交点的横坐标为2.5,
∴方程2x﹣5=0的解为x=2.5;
∵当x>2.5时,一次函数y=2x﹣5的图象在x轴上方,即2x﹣5>0,
∴不等式2x﹣5>0的解集是x>2.5.
【分析】根据一次函数与一元一次方程的关系,根据一次函数y=2x﹣5的图象,可写出一元一次方程2x﹣5=0,直线与x轴交点的横坐标的值即为方程的解;
根据一次函数与一元一次不等式的关系,根据一次函数y=2x﹣5的图象,可写出一元一次不等式2x﹣5>0,直线在x轴上方的部分对应的x的取值范围就是不等式的解集.
23.解:函数y=ax+b,y随x增大而减少,且交x轴于A(3,0),得
a<0,b>0,3a+b=0,
b=﹣3a.
把b=﹣3a代入(a﹣b)x﹣2b<0,得
4ax+6a<0.
解得x>﹣.
【分析】根据函数的性质、函数与x轴的交点,可得a、b的关系,根据不等式的性质,可得答案.
24.
解:(1)当两函数图象相交时,两家旅行社收费相同,由图象知为30人
(2)由图象知:当有30人以下时,y1<y2
,
所以选择甲旅行社合算
(3)由图象知:当有50人参加时,y1>y2
,
所以选择乙旅行社合算
【分析】(1)当两函数图象相交时,两家旅行社收费相同,由图象即可得出答案.(2)由图象比较收费y1、y2
,
即可得出答案.(3)当有50人时,比较收费y1、y2
,
即可得出答案.
25.
解:(1)当x=﹣2时,y=0,
所以方程kx+b=0的解为x=﹣2
(2)当x>2时,y>2,
所以不等式kx+b>2的解集为x>2
(3)﹣2≤m≤2,0≤n≤2
【分析】(1)根据一次函数图象与x轴的交点为(-2,0),从而求出方程kx+b=0的解.
(2)根据图象可知当x=2时,y=2且y随x的增大而增大,据此可求出不等式kx+b>2的解集.
(3)根据图形可得线段AB图象的自变量的取值范围是﹣2≤x≤2,利用一次函数的增减性可得函数值的范围0≤y≤2,据此可分别求出m、n的范围.
26.解:(1)函数y1=﹣2x﹣3与x轴和y轴的交点分别是(﹣1.5,0)和(0,﹣3),y2=x+2与x轴和y轴的交点分别是(﹣4,0)和(0,2),其图象如图:
(2)观察图象可知,函数y1=﹣2x﹣3与y2=x+2交于点(﹣2,1),当x<﹣2时,直线y1=﹣2x﹣3的图象落在直线y2=x+2的上方,即﹣2x﹣3>x+2,所以不等式﹣2x﹣3>x+2的解集为x<﹣2;故答案为x<﹣2;(3)∵y1=﹣2x﹣3与y2=x+2与y轴分别交于点A(0,﹣3),B(0,2),∴AB=5,∵y1=﹣2x﹣3与y2=x+2交于点C(﹣2,1),∴△ABC的边AB上的高为2,∴S△ABC=×5×2=5.
【分析】(1)先求出直线y1=﹣2x﹣3,y2=x+2与x轴和y轴的交点,再画出两函数图象即可;
(2)直线y1=﹣2x﹣3的图象落在直线y2=x+2上方的部分对应的x的取值范围就是不等式﹣2x﹣3>x+2的解集;
(3)根据三角形的面积公式求解即可.
27.【答案】
(1)60;4
解:(2)由点(3,90)求得,y2=30x.
当0.5<x≤2时,设解析式为y1=ax+c,
由点(0.5,0),(2,90)则,
解得:
∴y1=60x-30,
当y1=y2时,60x-30=30x,解得,x=1.
此时y1=y2=30.
所以点P的坐标为(1,30)
(3)①当x≤0.5时,依题意,(-60x+30)+30x≤8.解得,x≥
.不合题意.
②当0.5<x≤1时,依题意,30x-(60x-30)≤8
解得,x≥
.所以
≤x≤1.
③当1<x≤2时,依题意,(60x-30)-30x≤8
解得,x≤
.所以1<x≤
④当2<x≤3时,甲船已经到了而乙船正在行驶,
∵90-30x≤8,解得x≥
,
所以,当
≤x≤3,甲、乙两船可以相互望见;
综上所述,当
≤x≤
或
≤x≤
时,
甲、乙两船可以相互望见
27.
解:(1)解:A、C两港口间距离s=30+90=120(km),
又由于甲船行驶速度不变,
故30÷0.5=60(km/h),
则a=2(h)
【分析】(1)由甲船行驶的函数图象可以看出,甲船从A港出发,0.5h后到达B港,ah后到达C港,又由于甲船行驶速度不变,则可以求出a的值;(2)分别求出0.5h后甲乙两船行驶的函数表达式,联立即可求解;(3)将该过程划分为0≤x≤0.5、0.5<x≤1、x>1三个范围进行讨论,得到能够相望时x的取值范围.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020年暑期衔接训练青岛版数学八年级下册:第18讲
一次函数
与一元一次不等式
一、单选题:
1.已知函数
,当
时,y的取值范围是(????
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
2.如图,函数
和
的图象相交于点
,则关于x的不等式
的解集是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为(??
)
A.?x≤3????????????????????????????????????B.?x≥3????????????????????????????????????C.?x≤
????????????????????????????????????D.?x≥
4.某便利店的咖啡单价为10元/杯,为了吸引顾客,该店共推出了三种会员卡,如下表:
会员卡类型
办卡费用/元
有效期
优惠方式
A类
40
1年
每杯打九折
B类
80
1年
每杯打八折
C类
130
1年
一次性购买2杯,第二杯半价
例如,购买A类会员卡,1年内购买50次咖啡,每次购买2杯,则消费
元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为(???
)
A.?购买A类会员卡????????????B.?购买B类会员卡?????????????C.?购买C类会员卡????????????D.?不购买会员卡
5.如图,一次函数
的图象经过点
,则关于
的不等式
的解集为(???
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
6.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是(???
)
A.?0???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
7.如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为0,AB⊥x轴于点B,△AOB的面积为3,则满足y1
A.?x>2??????????????????????????????????????B.?x<2??????????????????????????????????????C.?x>3??????????????????????????????????????D.?x<3
8.如图,已知直线
过点
,过点
的直线
交
轴于点
,则关于的不等式组
的解集为(???
)
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
9.如图,函数
和
的图象相交于点
,则关于
的不等式
的解集为(??
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
10.如图,在平面直角坐标系中,己知点A(1,3)、B(n,3),若直线y=2x与线段AB有公共点,则n的值不可能是(???
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
11.若方程2x=4的解使关于x的一次不等式(a-1)x<a+5成立,则a的取值范围是( )
A.?a≠1?????????????????????????????????B.?a>7?????????????????????????????????C.?a<7?????????????????????????????????D.?a<7且a≠1
12.已知一次函数y=ax+b的图象过第一、二、四象限,且与x轴交于点(2,0),则关于x的不等式a(x-1)-b>0的解集为(??
)
A.?x<-1??????????????????????????????????B.?x>-1??????????????????????????????????C.?x>1??????????????????????????????????D.?x<1
二、填空题:
13.已知
,
,当
时,x的取值范围是________.
14.如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2.则下列结论:①m<0,n>0;②直线y=nx+4n一定经过点(-4,0);③m与n满足m=2n-2;④当x>-2时,nx+4n>-x+m,其中正确结论的个数是________个.
15.如图,直线y=kx+b(k、b是常数k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为________.
16.直线y=kx和y=ax+4交于A(1,k),则不等式kx-6
与y=kx+b(k、b为常数,且k≠0)的图像相交于点A(m,-2),则m=________,关于x的不等式组
?的解是________。
18.一次函数y=kx+b的图象经过A(-1,1)和B(-
?,0),则不等式组
的解为________.
19.若直线y=kx+k+1经过点(m
,
n+2)和(m+1,2n﹣1),且0<k<2,n是整数,则n=________.
20.如图,直线
过点A(0,2),且与直线
交于点P(1,m),则不等式组
>
>
-2的解集是________
?
三、解答题:
21.已知x2+ax+3=(x﹣1)(x﹣b),试求直线y=2x﹣a与直线y=bx+3的交点坐标,并直接写出关于x的不等式2x﹣a≥bx+3的解集.
22.如图是一次函数y=2x﹣5的图象,请根据给出的图象写出一个一元一次方程和一个一元一次不等式,并用图象求解所写出的方程和不等式.
23.已知函数y=ax+b,y随x增大而减少,且交x轴于A(3,0),求不等式(a﹣b)x﹣2b<0的解集.
24.学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2
,
且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)当参加老师的人数为多少人时,选择甲旅行社合算?
(3)如果全共有50人参加时,选择哪家旅行社合算?
25.如图,直线l是一次函数y=kx+b的图象,点A、B在直线l上,根据图象回答下列问题:
(1)写出方程kx+b=0的解;
(2)写出不等式kx+b>2的解集;
(3)若直线l上的点P(m
,
n)在线段AB上移动,则m、n的取值范围分别是什么?
26.已知一次函数y1=﹣2x﹣3与y2=x+2.
(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3>x+2的解集为多少?
(3)求两图象和y轴围成的三角形的面积.
27.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1
、y2
(km),
y1
、y2
与x的函数关系如图所示.
(1)填空:A、C两港口间的距离为________km,
________;
(2)求图中点P的坐标;
(3)若两船的距离不超过8km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
答案解析部分
一、单选题
1.【答案】
C
解:
,因为k<0,所以y随x的增大而减小.
当x=-1时,y=
;当x=1时,y=
.
所以当
时,y的取值范围是
.
故答案为:C.
【分析】由k=<0可知y随x的增大而减小,据此由x的取值范围即可得y的取值范围。
2.【答案】
A
解:
函数
和
的图象相交于点
,
不等式
的解集为
.
故选A
.
【分析】以交点为分界,结合图象写出不等式mx>x+3的解集即可.
3.【答案】D
解:∵函数y=2x的图象过点A(m,3),
∴将点A(m,3)代入y=2x得,2m=3,
解得,m=
,
∴点A的坐标为(
,3),
∴由图可知,不等式2x≥ax+4的解集为x≥
.
故选:D.
【分析】首先利用待定系数法求出A点坐标,再以交点为分界,结合图象写出不等式2x≥ax+4的解集即可.
4.【答案】
C
解:设一年内在该便利店买咖啡的次数为x次,消费的钱数为y元,根据题意得:yA=40+0.9
x=40+18x,yB=80+0.8
x=80+16x,yC=130+15
=130+15x,
当75≤x≤85时,
1390≤yA≤1570;
1280≤yB≤1440;
1255≤yC≤1405;
由此可见,C类会员年卡消费最低,所以最省钱的方式为购买C类会员年卡.
故答案为:C.
【分析】设一年内在该便利店买咖啡的次数为x次,消费的钱数为y元,根据题意得:列出3类会员卡用含x的关系表示消费的费用y,再确定y的范围,进行比较即可解答.
5.【答案】
A
解:∵
,
,
∴kx+b<-3即y<-3,
∵一次函数
的图象经过点B(4,-3),
∴当x=4时y=-3,
由图象得y随x的增大而减小,当
时,y<-3,
故答案为:A.
【分析】由
即y<-3,根据图象即可得到答案.
6.【答案】
B
解:∵y1=kx+b的函数值随x的增大而减小,
∴k<0;故①符合题意
∵y2=x+a的图象与y轴交于负半轴,
∴a<0;
当x<3时,相应的x的值,y1图象均高于y2的图象,
∴y1>y2
,
故②③不符合题意.
故答案为:B.
【分析】根据y1=kx+b和y2=x+a的图象可知:k<0,a<0,当x<3时,y1>y2
,
可得出①符合题意,②③不符合题意,即可求解.
7.【答案】
B
解:因为△AOB的面积为3,函数y1=kx(k>0)和y2=ax+4(a<0)
的图象相交于点4(m,3),
可得:
·3m=3,解得:m=2,
所以满足y1
【分析】利用点A的坐标和△AOB的面积为3,建立关于m的方程,解方程求出m的值,可得到点A的坐标,然后观察函数图像可求出满足y1
D
解:过点A作AC
y轴,交x轴于点C,
∵
,
∴C(-2,0),
根据图象可知:直线AC与y轴之间的函数图像上的点所对应的x的取值范围(包含-2,不包含0)就是关于x的不等式组
的解集,
∴不等式组
的解集是:
.
故答案为:D.
【分析】根据关于x的不等式组
的解集与一次函数图象之间的关系,即可得到答案.
9.【答案】
A
解:∵函数y=?4x和y=kx+b的图象相交于点A(m,?8),
∴?8=?4m,
解得:m=2,
故A点坐标为(2,?8),
∵kx+b>?4x时,(k+4)x+b>0,
则关于x的不等式(k+4)x+b>0的解集为:x>2.
故答案为:A.
【分析】直接利用函数图象上点的坐标特征得出m的值,再利用函数图象得出答案即可.
10.【答案】
A
解:∵直线y=2x与线段AB有公共点
∴2n≥3
解得
n≥
∵1<
∴n的值不可能是1.
故答案为:A.
【分析】当直线y=2x与线段AB有公共点时,直线y=2x的图象不能在直线y=3下方,据此列出不等式求出n的取值范围即可判断出结论。
11.【答案】
D
解:
解方程2x=4得:x=2,
∵(a-1)x<a+5,
当a-1>0时,x<
,
∴
>2,
∴1<a<7.
当a-1<0时,x>
∴
<2,
∴a<1.
则a的取值范围是a<7且a≠1.
故答案为:D
【分析】先求出方程2x=4的解,再根据不等式(a-1)x<a+5用a表示出x的取值范围,即可求出a的取值范围
12.【答案】
A
解:依题意作图,
可知直线从左往右下降,则a<0。直线交y轴于上半轴,说明b>0。把点(2,0)代入原式解得b=-2a.
所以代入a(x-1)-b>0得a(x-1)+2a>0.
解得a(x+1)>0。所以x+1<0.则不等式的解集为x<-1.
选A.
【点评】本题难度中等。作图辅助判断出a,b值的范围为解题关键。做这类题要注意数形结合的思想。
二、填空题
13.【答案】
解:因为
,既可以转化为不等式
经过解得不等式可以得到
故答案为:
【分析】把
,
,代入
,解不等式即可.
14.【答案】
4
解:①∵直线y=?x+m与y轴交于负半轴,∴m<0;
∵y=nx+4n(n≠0)的图象从左往右逐渐上升,∴n>0,
故结论①正确;
②将x=?4代入y=nx+4n,得y=?4n+4n=0,
∴直线y=nx+4n一定经过点(?4,0).
故结论②正确;
③∵直线y=?x+m与y=nx+4n(n≠0)的交点的横坐标为?2,
∴当x=?2时,y=2+m=?2n+4n,
∴m=2n?2.
故结论③正确;
④∵当x>?2时,直线y=nx+4n在直线y=?x+m的上方,
∴当x>?2时,nx+4n>?x+m,
故结论④正确.
故答案为:4.
【分析】①由直线y=?x+m与y轴交于负半轴,可得m<0;y=nx+4n(n≠0)的图象从左往右逐渐上升,可得n>0,即可判断结论①正确;②将x=?4代入y=nx+4n,求出y=0,即可判断结论②正确;③代入交点坐标整理即可判断结论③正确;④观察函数图象,可知当x>?2时,直线y=nx+4n在直线y=?x+m的上方,即nx+4n>?x+m,即可判断结论④正确.
15.【答案】
x<4
解:∵直线y=kx+b与直线y=2交于点A(4,2),
∴x<4时,y<2,
∴关于x的不等式kx+b<2的解集为x<4.
故答案为
:x<4.
【分析】观察函数图象,写出直线y=kx+2在直线y=2下方所对应的自变量的范围即可.
16.【答案】
1
∴a+4=k
∴a=k-4,
kx-6<(k-4)x+4
∴kx-6<(k-4)x+4
解之:x,
由图像可知当x>1时,kx>ax+4,
∴当1<x<2.5时,kx-6
【分析】由题意可知将点A的坐标代入y=ax+4,可得到a=k-4,再由kx-6
-3;
-
解得m=-3,
则由图象可得当x<-3时,kx+b<-x-6,
当-x-6=0,
解得x=-,
由图象可得当x>-时,y=-x-6<0,
综上不等式组的解集为:-
即kx+b<-x-6,
令y=-x-6=0,
求出其与x轴的交点,可得x>-时,y=-x-6的图象在x轴下方,即y<0,
两者结合即可得出不等式组的解集.
18.【答案】
-
<x<-1
解:由题意可得:一次函数图象在y=1的下方时x<-1,在y=0的上方时x>-
,
∴关于x的不等式0<kx+b<1的解集是-
<x<-1.
故答案为:-
<x<-1.
【分析】首先利用图象可找到图象在y=1的下方时,x<-1,在y=0的上方时x>-,
进而得到关于x的不等式0
19.【答案】
4
解:依题意得:
,
∴k=n﹣3,
∵0<k<2,
∴0<n﹣3<2,
∴3<n<5,
∵n是整数,则n=4
故答案为4.
【分析】将两点代入直线解析式,解出n的取值范围,得出n的取值。
20.【答案】
1<x<2
解:由于直线
过点A(0,2),P(1,m),
则
,解得
,
,
故所求不等式组可化为:
mx>(m-2)x+2>mx-2,
0>-2x+2>-2,
解得:1<x<2,
【分析】根据待定系数法,用含m的代数式表示函数,
根据题意,列出关于x的不等式组,进而求解.
三、解答题
21.
解:∵x2+ax+3=(x﹣1)(x﹣b)=x2﹣(b+1)x+b,
∴b=3,a=﹣(b+1)=﹣4.
联立两函数解析式成方程组,
,解得:
,
∴直线y=2x+4与直线y=3x+3的交点坐标为(1,6).
画出两直线,如图所示,
观察函数图象可知,当x<1时,直线y=2x+4在直线y=3x+3的上方,
∴不等式2x+4≥3x+3的解集为x≤1.
【分析】根据给定等式可求出a、b的值,联立两函数解析式成方程组,通过解方程组可求出两直线的交点坐标,画出两直线,根据直线的上下位置关系,即可得出不等式2x+4≥3x+3的解集.
22.解:根据给出的图象可写出一个一元一次方程为2x﹣5=0,一个一元一次不等式为2x﹣5>0.
∵一次函数y=2x﹣5的图象与x轴交点的横坐标为2.5,
∴方程2x﹣5=0的解为x=2.5;
∵当x>2.5时,一次函数y=2x﹣5的图象在x轴上方,即2x﹣5>0,
∴不等式2x﹣5>0的解集是x>2.5.
【分析】根据一次函数与一元一次方程的关系,根据一次函数y=2x﹣5的图象,可写出一元一次方程2x﹣5=0,直线与x轴交点的横坐标的值即为方程的解;
根据一次函数与一元一次不等式的关系,根据一次函数y=2x﹣5的图象,可写出一元一次不等式2x﹣5>0,直线在x轴上方的部分对应的x的取值范围就是不等式的解集.
23.解:函数y=ax+b,y随x增大而减少,且交x轴于A(3,0),得
a<0,b>0,3a+b=0,
b=﹣3a.
把b=﹣3a代入(a﹣b)x﹣2b<0,得
4ax+6a<0.
解得x>﹣.
【分析】根据函数的性质、函数与x轴的交点,可得a、b的关系,根据不等式的性质,可得答案.
24.
解:(1)当两函数图象相交时,两家旅行社收费相同,由图象知为30人
(2)由图象知:当有30人以下时,y1<y2
,
所以选择甲旅行社合算
(3)由图象知:当有50人参加时,y1>y2
,
所以选择乙旅行社合算
【分析】(1)当两函数图象相交时,两家旅行社收费相同,由图象即可得出答案.(2)由图象比较收费y1、y2
,
即可得出答案.(3)当有50人时,比较收费y1、y2
,
即可得出答案.
25.
解:(1)当x=﹣2时,y=0,
所以方程kx+b=0的解为x=﹣2
(2)当x>2时,y>2,
所以不等式kx+b>2的解集为x>2
(3)﹣2≤m≤2,0≤n≤2
【分析】(1)根据一次函数图象与x轴的交点为(-2,0),从而求出方程kx+b=0的解.
(2)根据图象可知当x=2时,y=2且y随x的增大而增大,据此可求出不等式kx+b>2的解集.
(3)根据图形可得线段AB图象的自变量的取值范围是﹣2≤x≤2,利用一次函数的增减性可得函数值的范围0≤y≤2,据此可分别求出m、n的范围.
26.解:(1)函数y1=﹣2x﹣3与x轴和y轴的交点分别是(﹣1.5,0)和(0,﹣3),y2=x+2与x轴和y轴的交点分别是(﹣4,0)和(0,2),其图象如图:
(2)观察图象可知,函数y1=﹣2x﹣3与y2=x+2交于点(﹣2,1),当x<﹣2时,直线y1=﹣2x﹣3的图象落在直线y2=x+2的上方,即﹣2x﹣3>x+2,所以不等式﹣2x﹣3>x+2的解集为x<﹣2;故答案为x<﹣2;(3)∵y1=﹣2x﹣3与y2=x+2与y轴分别交于点A(0,﹣3),B(0,2),∴AB=5,∵y1=﹣2x﹣3与y2=x+2交于点C(﹣2,1),∴△ABC的边AB上的高为2,∴S△ABC=×5×2=5.
【分析】(1)先求出直线y1=﹣2x﹣3,y2=x+2与x轴和y轴的交点,再画出两函数图象即可;
(2)直线y1=﹣2x﹣3的图象落在直线y2=x+2上方的部分对应的x的取值范围就是不等式﹣2x﹣3>x+2的解集;
(3)根据三角形的面积公式求解即可.
27.【答案】
(1)60;4
解:(2)由点(3,90)求得,y2=30x.
当0.5<x≤2时,设解析式为y1=ax+c,
由点(0.5,0),(2,90)则,
解得:
∴y1=60x-30,
当y1=y2时,60x-30=30x,解得,x=1.
此时y1=y2=30.
所以点P的坐标为(1,30)
(3)①当x≤0.5时,依题意,(-60x+30)+30x≤8.解得,x≥
.不合题意.
②当0.5<x≤1时,依题意,30x-(60x-30)≤8
解得,x≥
.所以
≤x≤1.
③当1<x≤2时,依题意,(60x-30)-30x≤8
解得,x≤
.所以1<x≤
④当2<x≤3时,甲船已经到了而乙船正在行驶,
∵90-30x≤8,解得x≥
,
所以,当
≤x≤3,甲、乙两船可以相互望见;
综上所述,当
≤x≤
或
≤x≤
时,
甲、乙两船可以相互望见
27.
解:(1)解:A、C两港口间距离s=30+90=120(km),
又由于甲船行驶速度不变,
故30÷0.5=60(km/h),
则a=2(h)
【分析】(1)由甲船行驶的函数图象可以看出,甲船从A港出发,0.5h后到达B港,ah后到达C港,又由于甲船行驶速度不变,则可以求出a的值;(2)分别求出0.5h后甲乙两船行驶的函数表达式,联立即可求解;(3)将该过程划分为0≤x≤0.5、0.5<x≤1、x>1三个范围进行讨论,得到能够相望时x的取值范围.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
