【2020年暑期衔接】青岛版八下 第20讲 一次函数单元测试题(含解析)
文档属性
| 名称 | 【2020年暑期衔接】青岛版八下 第20讲 一次函数单元测试题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 557.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2020年暑期衔接训练青岛版数学八年级下册:第20讲
《一次函数》测试
一、单选题:
1.下列函数:(1)
y=x
;(2)
;(3)
;(4)
;(5)s=12t;(6)y=30-4x中,是一次函数的有??
(
???)
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
2.已知一次函数y=(m+1)x+m2-1
(m为常数),若图象过原点,则m(?????
)
A.?m=-1??????????????????????????????????B.?m=±1??????????????????????????????????C.?m=0??????????????????????????????????D.?m=1
3.下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是(??
)
A.??????????B.???????????C.??????????D.?
4.公式
表示当重力为P时的物体作用在弹簧上时弹簧的长度.
表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是(
??)
A.?L=10+0.5P????????????????????????B.?L=10+5P????????????????????????C.?L=80+0.5P????????????????????????D.?L=80+5P
5.图中两直线
,
的交点坐标可以看作方程组(?
??)的解.
A.???????????????????B.???????????????????C.???????????????????D.?
6.如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是(???
)
A.?1?????????????????????????????B.?1?????????????????????????????C.?1?????????????????????????????D.?17.如图,在矩形MNPO中(如图1),动点R从点N出发,沿N→P→O→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPO的周长是(????
)
A.?11?????????????????????????????????????????B.?15?????????????????????????????????????????C.?16?????????????????????????????????????????D.?24
8.如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有( )
A.?5个??????????????????????????????????????B.?4个???????????????????????????????????????C.?3个??????????????????????????????????????D.?2个
9.已知平面内有两条直线l1:y=x+2,l2:y=-2x+4交于点A,与x轴分别交于B,C两点,P(m,2m-1)落在△ABC内部(不含边界),则m的取值范围是(??
)
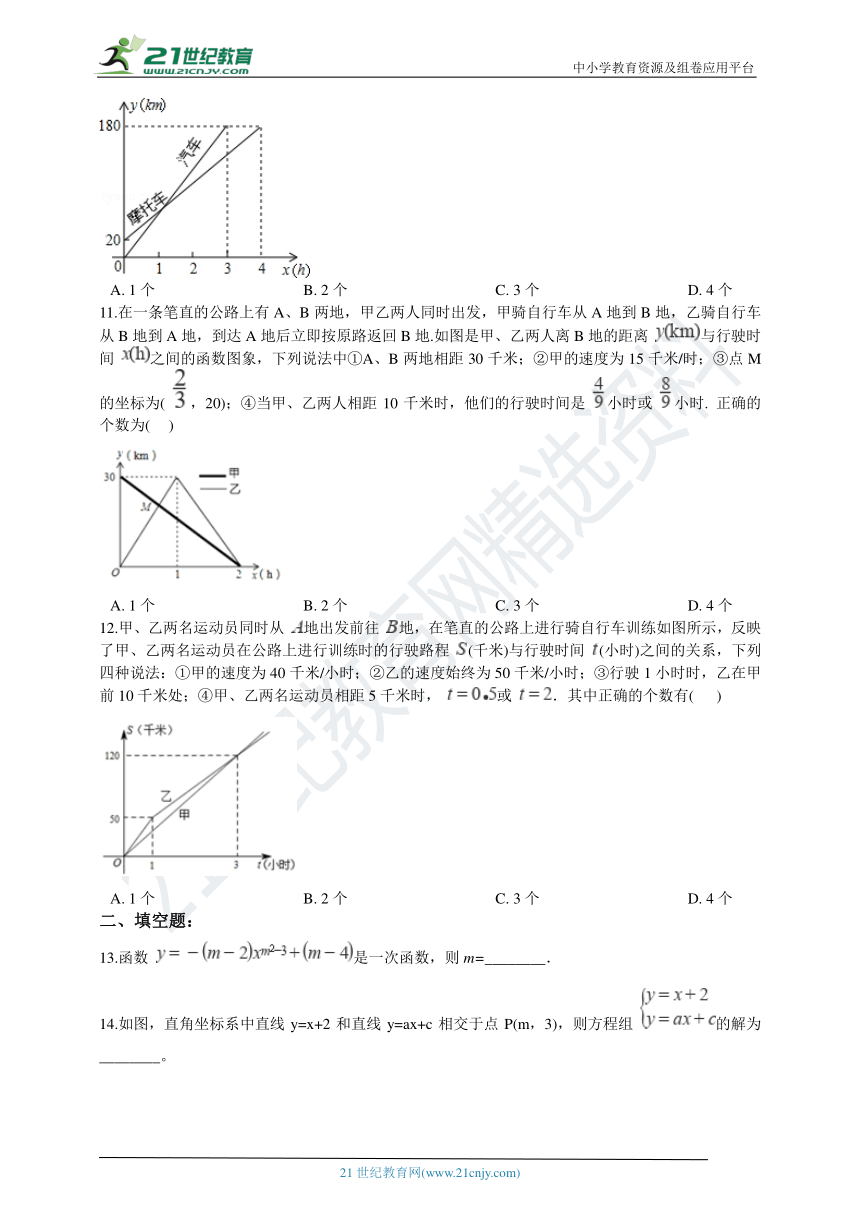
A.?-2????????????????????????C.?0????????????????????????D.?-210.一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:
①摩托车比汽车晚到lh;②A、B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1h后与摩托车相遇,此时距B地40km.其中正确结论的个数是(??
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
11.在一条笔直的公路上有A、B两地,甲乙两人同时出发,甲骑自行车从A地到B地,乙骑自行车从B地到A地,到达A地后立即按原路返回B地.如图是甲、乙两人离B地的距离
与行驶时间
之间的函数图象,下列说法中①A、B两地相距30千米;②甲的速度为15千米/时;③点M的坐标为(
,20);④当甲、乙两人相距10千米时,他们的行驶时间是
小时或
小时.
正确的个数为(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
12.甲、乙两名运动员同时从
地出发前往
地,在笔直的公路上进行骑自行车训练如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程
(千米)与行驶时间
(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时,
或
.其中正确的个数有(????
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题:
13.函数
是一次函数,则m=________.
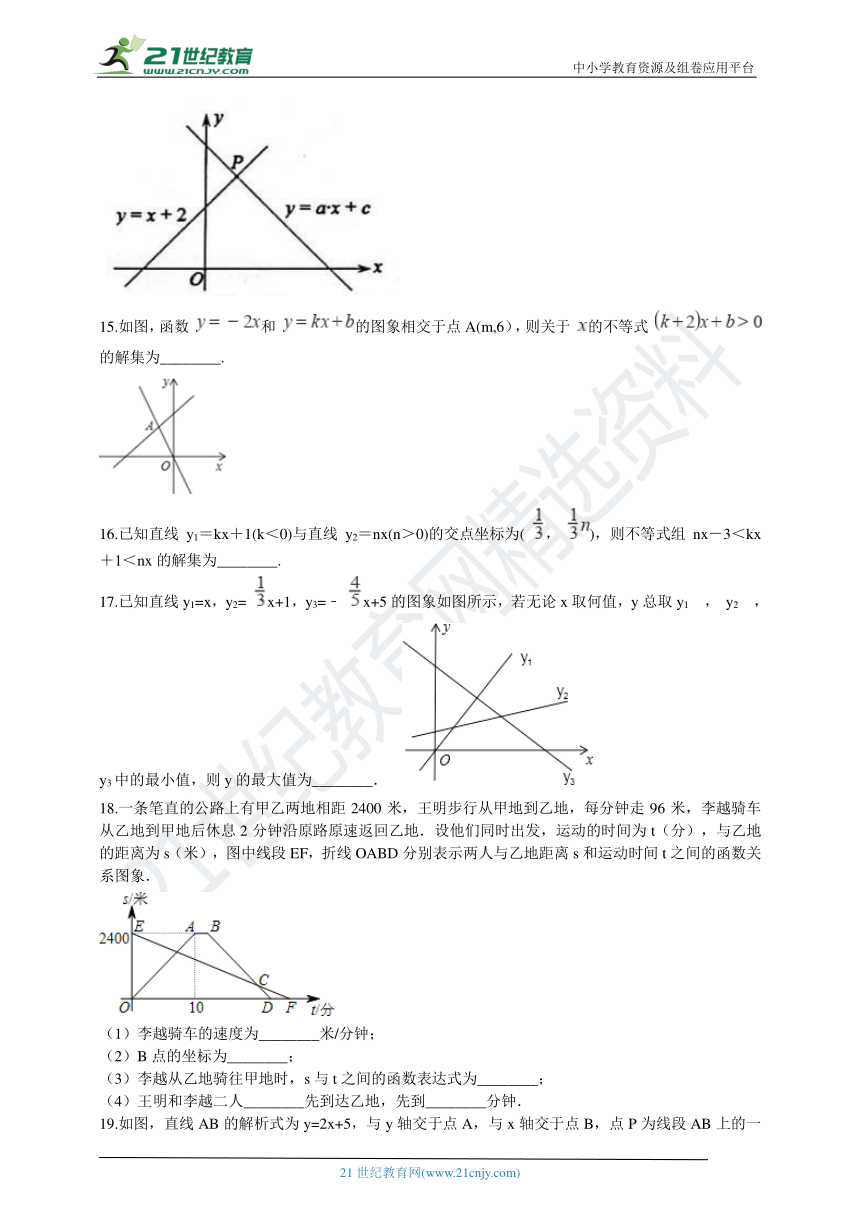
14.如图,直角坐标系中直线y=x+2和直线y=ax+c相交于点P(m,3),则方程组
的解为________。
15.如图,函数
和
的图象相交于点A(m,6),则关于
的不等式
的解集为________.
16.已知直线y1=kx+1(k<0)与直线y2=nx(n>0)的交点坐标为(
,
),则不等式组nx-3<kx+1<nx的解集为________.
17.已知直线y1=x,y2=
x+1,y3=﹣
x+5的图象如图所示,若无论x取何值,y总取y1
,
y2
,
y3中的最小值,则y的最大值为________.
18.一条笔直的公路上有甲乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地.设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象.
(1)李越骑车的速度为________米/分钟;
(2)B点的坐标为________;
(3)李越从乙地骑往甲地时,s与t之间的函数表达式为________;
(4)王明和李越二人________先到达乙地,先到________分钟.
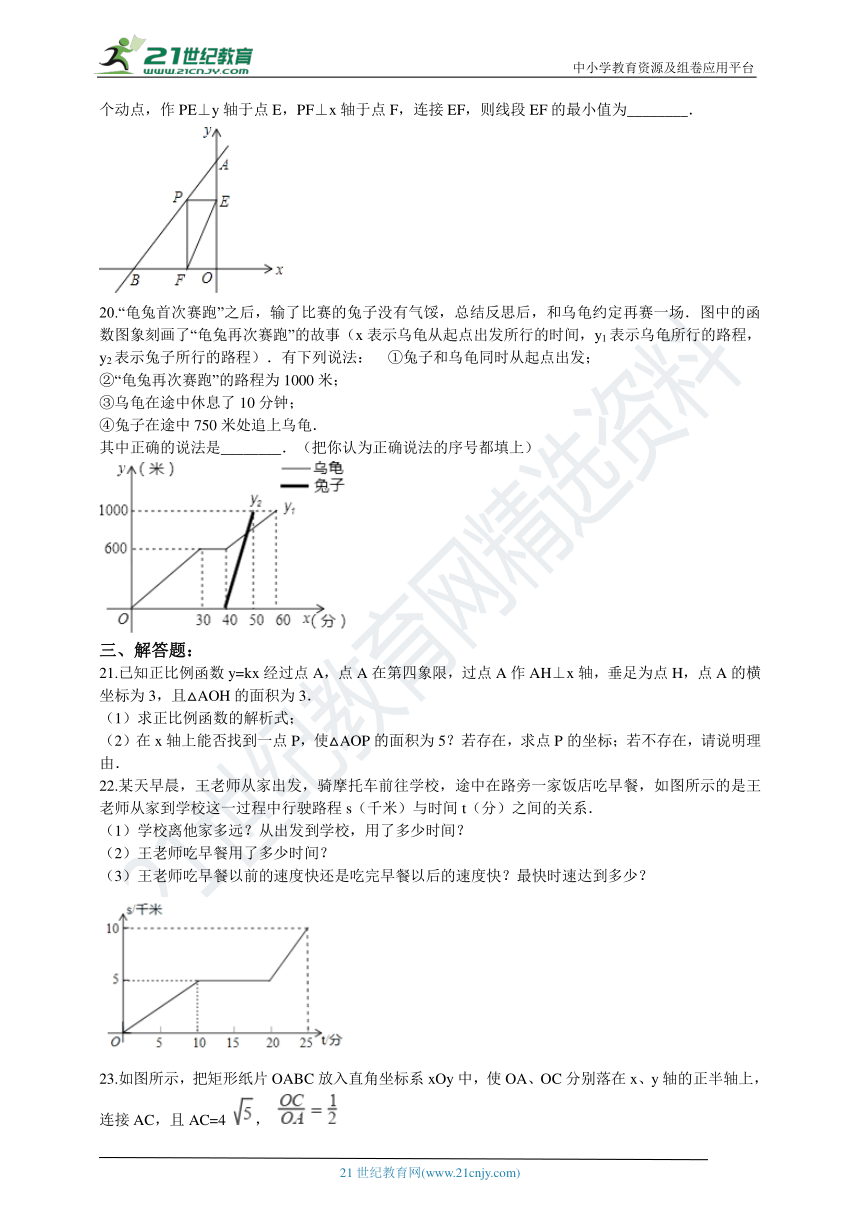
19.如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为________.
20.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①兔子和乌龟同时从起点出发;
②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是________.(把你认为正确说法的序号都填上)
三、解答题:
21.已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
22.某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
23.如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4
,
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.
24.(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx﹣2(m﹣1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为2,求m值.
四、综合题:
25.某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天)
豪华间(元/人/天)
贵宾间(元/人/天)
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了________人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;________
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
26.某产品生产车间有工人10名,已知每名工人每天可生产甲种产品10个或乙种产品12个,且每生产一个甲种产品可获得利润100元,每生产一个乙种产品可获得利润150元.在这10名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品.
(1)求出此车间每天获取利润y(元)与x(人)之间的函数关系式;
(2)若要使此车间每天获取利润为14800元,要派多少名工人去生产甲种产品?
(3)若要使此车间每天获取利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适?
27.在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900
,
且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。
28.为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动,自行车队从甲地出发,目的地为乙地,在自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地。自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的3倍,如图所示的是自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地的时间x(h)的关系图象,请根据图象提供的信息,回答下列问题:
(1)自行车队行驶的速度是________;邮政车行驶的速度是________;a=________。
(2)邮政车出发多少小时与自行车队相遇?
(3)当邮政车与自行车队相距15km时,此时离邮政车出发经过了多少小时?
答案解析部分
一、单选题
1.【答案】
D
解:(1)
y=x,是一次函数
;(2)
,是一次函数;(3)
,不是一次函数;(4)
,是一次函数;(5)s=12t,是一次函数;(6)y=30-4x,是一次函数,共5个.
故答案为:D.
【分析】直接利用一次函数的一般形式y=kx+b(k≠0)分析得出答案.
2.【答案】
D
解:∵一次函数y=(m+1)x+m2-1(m为常数)的图象过原点,
∴m2-1=0,解得m=±1.
∵此函数是一次函数,
∴m+1≠0,解得m≠-1,
∴m=1.
故答案为:D.
【分析】将(0,0)代入一次函数解析式中,可得m2-1=0,解得m=±1.根据一次函数的定义可知m≠-1,据此解答即可.
3.【答案】
A
解:A、由一次函数图象可知:
,
,则此时
,
由正比例函数图象可得:
,故该选项正确;
B、由一次函数图象可知:
,
,则此时
,
由正比例函数图象可得:
,互相矛盾,故该选项错误;
C、由一次函数图象可知:
,
,则此时
,
由正比例函数图象可得:
,互相矛盾,故该选项错误;
D、由一次函数图象可知:
,
,则此时
,
由正比例函数图象可得:
,互相矛盾,故该选项错误.
故答案为:A.
【分析】根据一次函数图象与系数的关系以及正比例函数图象与系数的关系逐一对各选项进行判断,然后进一步得出答案即可.
4.【答案】
A
解:A和B中,L0=10,表示弹簧短;A和C中,K=0.5,表示弹簧硬;
故答案为:A
【分析】A和B中,L0=10,表示弹簧短;A和C中,K=0.5,表示弹簧硬,由此即可得出结论.
5.【答案】
B
解:根据图象可求出直线
,
的解析式分别为:
,所以两直线的交点坐标可以看作方程组
的解,
故答案为:B.
【分析】通过观察图像得出l1,l2的k、b值,求出解析式,两个直线的交点就可以看作两个方程的解。
6.【答案】
C
解:∵直线y1=kx+b过点A(0,3)和点P(1,m),
∴0+b=3,k+b=m
∴b=3,k=m-3
∴(m-3)x+3>mx-2
mx-3x+3>mx-2
解之:
∵点P(1,m)
∴mx>kx+b>mx-2的解集为.
故答案为:C
【分析】由题意可知直线y1=kx+b过点A(0,3)和点P(1,m),将这两点代入函数解析式,可得到k=m-3,再将k的值代入不等式,可得到mx-3x+3>mx-2,解不等式可得到x的取值范围,再根据点P的横坐标,就可得到不等式组的解集。
7.【答案】
C
解:∵x=3时,及R从N到达点P时,面积开始不变,
∴PN=3,同理可得OP=5,
∴矩形的周长为2×(3+5)=16.
故选C.
8.【答案】
B
解:①以A为直角顶点,可过A作直线垂直于AB,与y轴交于一点,这一点符合点P的要求;
②以B为直角顶点,可过B作直线垂直于AB,与y轴交于一点,这一点也符合P点的要求;
③以P为直角顶点,与y轴共有2个交点.
所以满足条件的点P共有4个.
故选B.
【分析】当∠PBA=90°时,即点P的位置有2个;当∠ABP=90°时,点P的位置有1个;当∠BAP=90°时,在y轴上共有1个交点.
9.【答案】B
解:由题意得?
:
0<2m-1<m+2
①
;0<2m-1<-2m+4②?
;
解得?
:;
故应选?
B.
【分析】此题分两种情况①点P在x轴上方在直线l1右边;列出不等式0<2m-1<m+2,②点P在x轴上方在直线l2左边,列出不等式0<2m-1<-2m+4,解两不等式组成的不等式组,即可得出答案。
10.【答案】
C
解:摩托车比汽车晚到:4﹣3=1h,故①正确,
A、B两地的路程为20km,故②正确,
摩托车的速度为(180﹣20)÷4=40km/h,汽车的速度为180÷3=60km/h,故③错误,
设汽车出x小时与摩托车相遇,则60x=20+40x,得x=1,此时距离B地40×1=40km,故④正确,
故答案为:C
【分析】①中,根据汽车和摩托车用的时间,即可得到摩托车比汽车晚一个小时;
②中,根据时间为0时,二者的距离即为AB之间的距离;
③中,根据图象,分别求出摩托车和汽车的速度即可;
④中,当二者的路程一样时,为二者相遇的时间,继而求出与B地的距离即可。
11.【答案】
C
解:根据题意可以列出甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数关系得:
y甲=-15x+30
y乙=
由此可知,①②符合题意.
当15x+30=30x时,
解得x=
则M坐标为(
,20),故③符合题意.
当两人相遇前相距10km时,
30x+15x=30-10
x=
,
当两人相遇后,相距10km时,
30x+15x=30+10,
解得x=
15x-(30x-30)=10
解得x=
∴④不符合题意.
故答案为C.
【分析】根据题意,确定①-③符合题意,当两人相距10千米时,应有3种可能性.
12.【答案】
B
解:①甲的速度为
千米/小时,故符合题意;
②t≤1时,乙的速度为
千米/小时,t>1后,乙的速度为
千米/小时,故不符合题意;
③行驶1小时时,甲走了40千米,乙走了50千米,乙在甲前10千米处,故符合题意;
④∵甲的速度为40千米/小时:甲的函数表达式为:y=40x,
乙的函数表达为:0≤t≤1时,乙的速度为50千米/小时,∴y=50x,
t>1时,设y=kx+b,
将点(1,50),(3,120)代入得:
,解得k=35,b=15,
∴t>1时,y=35x+15,
t=0.5时,甲、乙两名运动员相距=50×
-40×
=5(千米),
t=2时,甲、乙两名运动员相距=(35×2+15)?2×40=5(千米),
同理t=4时,甲、乙两名运动员相距为5千米,故不符合题意.
故答案为:B.
【分析】①甲的速度为
千米/小时,即可求解;②t≤1时,乙的速度为50千米/小时,t>1后,乙的速度为
千米/小时,即可求解;③行驶1小时时,甲走了40千米,乙走了50千米,即可求解;④甲的函数表达式为:y=40x,乙的函数表达为:0≤t≤1时,y=50x,t>1时,y=35x+15,即可求解.
二、填空题
13.【答案】
-2
解:∵函数
是一次函数
∴
解得:m=-2
故答案为:-2.
【分析】根据一次函数的定义即可求出结论.
14.【答案】
解:将点P(m,3)代入直线y=x+2中,
得m+2=3,
∴m=1.
∴点P(1,3),
∴方程组??的解为?.
故答案为:
?.
【分析】将点P(m,3)代入直线y=x+2中,求出m的值,即得点P的坐标,点P的横纵坐标即是两直线解析式的相对应方程组的解.
15.【答案】
x>-3
解:∵函数y=-2x和y=kx+b的图象相交于点A(m,6),
∴6=-2m,
解得:m=-3,
故A点坐标为:(-3,6),
∵kx+b>-2x时,
∴(k+2)x+b>0,
则关于x的不等式(k+2)x+b>0的解集为:x>-3.
故答案为:x>-3.
【分析】直接利用函数图象上点的坐标特征得出m的值,再利用函数图象得出答案.
16.【答案】
解:把(
,
)代入y1=kx+1,可得
,
解得k=n-3,
代入不等式得nx-3<nx-3x+1<nx,
解得:
∴不等式组mx-2<kx+1<mx的解集为
。
故答案为:
。
【分析】根据一次函数的性质,将(
,
)代入y1=kx+1得k=n-3,将k=n-3,代入不等式组,求解即可得出该不等式的解集。
17.【答案】
解:如图,分别求出y1
,
y2
,
y3交点的坐标A(
,
);B(
,
);C(
,
)
当x<
,y=y1;
当
≤x<
,y=y2;
当
≤x<
,y=y2;
当x≥
,y=y3
.
∵y总取y1
,
y2
,
y3中的最小值,
∴y的取值为图中红线所描述的部分,
则y1
,
y2
,
y3中最小值的最大值为C点的纵坐标
,
∴y最大=
.
【分析】y始终取三个函数的最小值,y最大值即求三个函数的公共部分的最大值.
18.【答案】
(1)240
(2)(12,2400)
(3)s=240t
(4)李越;3
解:(1)由图象可得,李越骑车的速度为:2400÷10=240米/分钟,
故答案为:240;(2)由题意可得,10+2=12(分钟),
点B的坐标为(12,2400),
故答案为:(12,2400);(3)设李越从乙地骑往甲地时,s与t之间的函数表达式为:s=kt,
由题意得:2400=10k,得:k=240,
即李越从乙地骑往甲地时,s与t之间的函数表达式为:s=240t,
故答案为:s=240t;(4)由图象可知,李越先到达乙地,先到达:2400÷96-(10×2+2)=3(分钟),
故答案为:李越,3.
【分析】(1)由函数图象中的数据可以直接计算出李越骑车的速度;(2)根据题意和图象中点A的坐标可以直接写出点B的坐标;(3)根据函数图象中的数据和待定系数法,可得s与t的函数表达式;(4)根据函数图象可以得到谁先到达乙地,并求出先到几分钟.
19.【答案】
解:∵一次函数y=2x+5中,令x=0,则y=5,令y=0,则x=﹣
,
∴A(0,5),B(﹣
,0).
∵PE⊥y轴于点E,PF⊥x轴于点F,
∴四边形PEOF是矩形,且EF=OP,
∵O为定点,P在线段上AB运动,
∴当OP⊥AB时,OP取得最小值,此时EF最小,
∵A(0,5),点B坐标为(﹣
,0),
∴OA=5,O
B=
,
由勾股定理得:AB=
=
=
,
∴AB?OP=OA?OB,
∴OP=
=
=
.
故答案为:
.
【分析】在一次函数y=2x+5中,分别令x=0和y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,满足条件,由条件可证明△AOB∽△OPB,利用相似三角形的性质可求得OP的长,即可求得EF的最小值.
20.【答案】②③④
解:观察函数图象可得出:
①兔子出发的时间为40分,①错误;
②“龟兔再次赛跑”的路程为1000米,②正确;
③乌龟休息的时间为40﹣30=10(分钟),③正确;
④设y2=k2x+b2(k2≠0),在40≤x≤60时间段内y1=k1x+b1(k1≠0),
将(40,600)、(60,1000)代入y1=k1x+b1中,得:
,解得:
,
∴y1=20x﹣200(40≤x≤60).
同理可求出:y2=100x﹣4000(40≤x≤50).
令y1=y2
,
即20x﹣200=100x﹣4000,
解得:x=
,
∴y1=20x﹣200=20×
﹣200=750,
∴兔子在途中750米处追上乌龟,④正确.
故答案为:②③④.
【分析】①由兔子出发时的时间为40分可得出①错误;②观察函数图象即可得出“龟兔再次赛跑”的路程为1000米,即②正确;③用40﹣30即可得出乌龟在途中休息了10分钟,即③正确;④设y2=k2x+b2(k2≠0),在40≤x≤60时间段内y1=k1x+b1(k1≠0),观察函数图象找出点的坐标利用待定系数法即可求出两函数关系式,令y1=y2求出x值,再将其代入y1中即可得出兔子在途中750米处追上乌龟,即④正确.综上即可得出结论.
三、解答题
21.
解:(1)∵点A的横坐标为3,且△AOH的面积为3
∴点A的纵坐标为﹣2,点A的坐标为(3,﹣2),
∵正比例函数y=kx经过点A,
∴3k=﹣2解得k=-,
∴正比例函数的解析式是y=-x;
(2)∵△AOP的面积为5,点A的坐标为(3,﹣2),
∴OP=5,
∴点P的坐标为(5,0)或(﹣5,0).
【分析】(1)根据题意求得点A的坐标,然后利用待定系数法求得正比例函数的解析式;
(2)利用三角形的面积公式求得OP=5,然后根据坐标与图形的性质求得点P的坐标
22.
解:(1)依题意得:学校离王老师家有10千米,从出发到学校王老师用了25分钟;
(2)依题意得:王老师吃早餐用了10分钟;
(3)吃早餐以前的速度为:5÷10=0.5km/分钟,吃完早餐以后的速度为:(10﹣5)÷(25﹣20)=1km/分钟=60km/小时,
∴王老师吃完早餐以后速度快,最快时速达到60km/小时.
【分析】(1)由于骑摩托车前往学校,途中在路旁一家饭店吃早餐,那么行驶路程s(千米)与时间t(分)之间的关系图象中有一段平行x轴的线段,然后学校,根据图象可以直接得到结论;
(2)根据图象中平行x轴的线段即可确定王老师吃早餐用了多少时间;
(3)根据图象可以分别求出吃早餐以前的速度和吃完早餐以后的速度,然后比较即可得到结果.
23.
解:
(1)∵
,
∴
可设OC=x,则OA=2x,
在Rt△AOC中,由勾股定理可得OC2+OA2=AC2
,
∴x2+(2x)2=(4
)2
,
解得x=4或x=-4(不合题意,舍去),
∴OC=4,OA=8,
∴A(8,0),C(0,4),
设直线AC解析式为y=kx+b,
∴
,
解得:
,
∴直线AC解析式为y=
x+4
(2)由折叠的性质可知AE=CE,
设AE=CE=y,则OE=8-y,
在Rt△OCE中,由勾股定理可得OE2+OC2=CE2
,
∴(8-y)2+42=y2
,
解得y=5,
∴AE=CE=5,
∵∠AEF=∠CEF,∠CFE=∠AEF,
∴∠CFE=∠CEF,
∴CE=CF=5,
∴S△CEF=
CF?OC=
×5×4=10,
即重叠部分的面积为10;
(3)由(2)可知OE=3,CF=5,
∴E(3,0),F(5,4),
设直线EF的解析式为y=k′x+b′,
∴
,
解得:
?,
∴直线EF的解析式为y=2x-6
【分析】
(1)设OC=x,则OA=2x,在Rt△OCE中,在Rt△AOC中,利用勾股定理可得OC2+OA2=AC2
,
求得A(8,0),C(0,4),然后用待定系数法确定直线的解析式。
(2)由折叠的性质可知AE=CE,在Rt△OCE中,由勾股定理可得OE2+OC2=CE2
,
解得AE=CE=5:再利用BC//OA,得到∠CFE=∠CEF,所以CE=CF=5,然后根据三角形的面积公式计算S△CEF
(3)首先求出E、F两点的坐标,然后利用待定系数法求出直线EF所在的解析式。
24.
解:(1)当x≥0时,y=|x|=x,即y=x(x≥0),将x=0代入得:y=0;将x=1代入得:y=1,
当x≤0时,y=|x|=﹣x,即y=﹣x(x≤0),将x=0代入得:y=0;将x=﹣1代入得:y=1.
过点O(0,0),A(﹣1,1)作射线OA,过点0(0,0),B(1,1)作射线OB,
函数y=|x|的图象如图所示:
(2)∵y=mx﹣2(m﹣1)=m(x﹣2)+2,
∴x﹣2=0,y=2
∴x=2,y=2,
即函数图象过定点(2,2)
(3)如下图:
∵函数y=mx﹣2(m﹣1)的图象经过顶点(2,2)
∴OC==2.
∴OD?OC=2,
∴OD=,
所以点D的坐标为(﹣1,1).
将x=﹣1,y=1代入y=mx﹣2(m﹣1)得:m=.
【分析】(1)将函数y=|x|,变形为y=x(x≥0),y=﹣x(x≤0),然后利用两点法画出函数图象即可;
(2)将函数解析式变形为:y=(x﹣2)+2,从而可知直线经过点(2,2);
(3)首先由勾股定理求得OC的长,然后根据三角形的面积为2,可求得OD的长度,从而可得到点D的坐标,将点D的坐标代入函数解析式可求得m的值.
四、综合题
25.
解:(1)设三人间普通客房住了x间,双人间普通客房住了y间.根据题意得:
????
解得:
∴三人间普通客房住了8间,双人间普通客房住了13间
(2);根据题意得:
?
即
?。
(3)不是,由上述一次函数可知,y随x的增大而减小,当三人间住的人数大于24人时,所需费用将少于1510元
【分析】(1)根据题意找出相等的关系量,由共有50人的旅游团,三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元,得到方程组,求出三人间普通客房和双人间普通客房住的间数;(2)由三人间共住了x人,则双人间住了(
50
?
x
)人,根据题意得到得到等式y
=
25
x
+
35
(
50
?
x
);(3)由上述一次函数可知,y随x的增大而减小,当三人间住的人数大于24人时,所需费用将少于1510元.
26.
解:(1)设每天安排x名工人生产甲种产品,则有(10-x)人生产乙产品,
y=10x×100+12(10-x)×150=-800x+18000,
答:每天获取利润y(元)与x(人)之间的函数关系式为y=-800x+18000;
(2)当y=14800时,即:-800x+18000=14800,
解得:x=4,
答:安排4人生产甲产品;
(3)由题意得:
-800x+18000≥15600,
解得:x≤3,
当x≤3时,10-x≥7,
因此至少要派7名工人生产乙产品.
【分析】(1)根据利润计算方法分别表示出甲产品、乙产品的利润,最后求和即得y,(2)把y=14800代入y与x的函数关系式,求出x的值,(3)列不等式求出x的取值范围,进而求出生产乙产品的人数的取值范围,确定至少安排乙产品的人数.
27.(1)证明:∵△ABC是等腰直角三角形
∴∠ACB=900
,
AC=BC
∴∠ACO+∠BCE=900
BE⊥CE,∴∠BCE+∠CBE=900
∴∠ACO=∠CBE
∴△AOC≌△CEB
(2)解:∵△AOC≌△CEB
∴BE=OC=2,CE=OA=4
∴点B的坐标为(6,2)
又一次函数y=x+b经过点B(6,2)
∴2=6+b
∴b=-4
∴点D的坐标为(0,-4)
∴
在△ABD中,AD边上高的长度就是B点纵坐标的绝对值.
∴S△ABD=
×8×6=24
∴△ABD的面积为24
【分析】(1)由等腰直角三角形的性质可证得AC=BC,∠ACO=∠CBE,进而可证得△AOC≌△CEB;(2)由(1)的全等,可得B坐标,代入解析式,可求出b,进而求出D坐标,AD的长,AD边上高的长度就是B点纵坐标,进而求出面积.
28.解:(1)自行车的速度==20km/h,
邮政车的速度=20×3=60km/h,
a=+1=.
故答案为:20km/h,60km/h,.
(2)设邮政车出发x小时两车相遇,分两种情况:①首次相遇,由题意得20(x+1)=60x,解得x=
故邮政车出发
小时两车首次相遇
②邮政车在返程途中与自行车队再次相遇.
根据题意得20(x+1)+60x=140×2,解得x=
故邮政车出发
小时后,在返程途中与自行车队再次相遇
即邮政车出发后
小时或
小时与自行车队相遇.
(3)设离邮政车出发经过了m小时与自行车队相距15km
当m<
时,①当自行车队在邮政车前面时,20(m+1)-60m=15,解得m=
②当邮政车在自行车队前面时,60m-20(m+1)=15,解得m=
当m>
时,①邮政车从乙地返回,与自行车队未相遇,20(m+1)+60m-140=140-15,解得m=
②邮政车从乙地返回,与自行车队相遇后,20(m+1)+60m-140=140+15,解得m=
即邮政车与自行车队相距15km时,此时离邮政车出发经过了
小时或
小时或
小时或
小时。
【分析】(1)由图象可得,全程为140km,
自行车行驶全程用7小时,代入速度公式即可求值,于是邮政车的速度可求,走完全程的时间也可求,看图可知a值等于邮政车走完全程的时间再加1小时.
(2)
设邮政车出发x小时两车相遇,
分两种情况:①首次相遇,
邮政车行驶的路程为60x,
自行车行驶的路程为20(x+1),据此列方程求解即可;
②邮政车在返程途中与自行车队再次相遇,这时两者的路程之和正好等于全程的2倍,据此列方程即可求解.
(3)分两种情况讨论,其中每种情况又下分两种情况讨论,
设离邮政车出发经过了m小时与自行车队相距15km,则邮政车行驶的路程为60m,自行车行驶的路程为
20(m+1),?当邮政车在去乙地的途中分两种情况,
当自行车队在邮政车前面时,?可得20(m+1)-60m=15;当邮政车在自行车前面时,可得?60m-20(m+1)=15;当邮政车在返回的途中也分两种情况,
①邮政车从乙地返回,与自行车队未相遇,可得20(m+1)+60m-140=140-15,
?②邮政车从乙地返回,与自行车队相遇后,可得20(m+1)+60m-140=140+15,
分别列式求解即可.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020年暑期衔接训练青岛版数学八年级下册:第20讲
《一次函数》测试
一、单选题:
1.下列函数:(1)
y=x
;(2)
;(3)
;(4)
;(5)s=12t;(6)y=30-4x中,是一次函数的有??
(
???)
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
2.已知一次函数y=(m+1)x+m2-1
(m为常数),若图象过原点,则m(?????
)
A.?m=-1??????????????????????????????????B.?m=±1??????????????????????????????????C.?m=0??????????????????????????????????D.?m=1
3.下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是(??
)
A.??????????B.???????????C.??????????D.?
4.公式
表示当重力为P时的物体作用在弹簧上时弹簧的长度.
表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是(
??)
A.?L=10+0.5P????????????????????????B.?L=10+5P????????????????????????C.?L=80+0.5P????????????????????????D.?L=80+5P
5.图中两直线
,
的交点坐标可以看作方程组(?
??)的解.
A.???????????????????B.???????????????????C.???????????????????D.?
6.如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是(???
)
A.?1
)
A.?11?????????????????????????????????????????B.?15?????????????????????????????????????????C.?16?????????????????????????????????????????D.?24
8.如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有( )
A.?5个??????????????????????????????????????B.?4个???????????????????????????????????????C.?3个??????????????????????????????????????D.?2个
9.已知平面内有两条直线l1:y=x+2,l2:y=-2x+4交于点A,与x轴分别交于B,C两点,P(m,2m-1)落在△ABC内部(不含边界),则m的取值范围是(??
)
A.?-2
①摩托车比汽车晚到lh;②A、B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1h后与摩托车相遇,此时距B地40km.其中正确结论的个数是(??
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
11.在一条笔直的公路上有A、B两地,甲乙两人同时出发,甲骑自行车从A地到B地,乙骑自行车从B地到A地,到达A地后立即按原路返回B地.如图是甲、乙两人离B地的距离
与行驶时间
之间的函数图象,下列说法中①A、B两地相距30千米;②甲的速度为15千米/时;③点M的坐标为(
,20);④当甲、乙两人相距10千米时,他们的行驶时间是
小时或
小时.
正确的个数为(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
12.甲、乙两名运动员同时从
地出发前往
地,在笔直的公路上进行骑自行车训练如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程
(千米)与行驶时间
(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时,
或
.其中正确的个数有(????
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题:
13.函数
是一次函数,则m=________.
14.如图,直角坐标系中直线y=x+2和直线y=ax+c相交于点P(m,3),则方程组
的解为________。
15.如图,函数
和
的图象相交于点A(m,6),则关于
的不等式
的解集为________.
16.已知直线y1=kx+1(k<0)与直线y2=nx(n>0)的交点坐标为(
,
),则不等式组nx-3<kx+1<nx的解集为________.
17.已知直线y1=x,y2=
x+1,y3=﹣
x+5的图象如图所示,若无论x取何值,y总取y1
,
y2
,
y3中的最小值,则y的最大值为________.
18.一条笔直的公路上有甲乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地.设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象.
(1)李越骑车的速度为________米/分钟;
(2)B点的坐标为________;
(3)李越从乙地骑往甲地时,s与t之间的函数表达式为________;
(4)王明和李越二人________先到达乙地,先到________分钟.
19.如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为________.
20.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①兔子和乌龟同时从起点出发;
②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是________.(把你认为正确说法的序号都填上)
三、解答题:
21.已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
22.某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
23.如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4
,
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.
24.(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx﹣2(m﹣1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为2,求m值.
四、综合题:
25.某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天)
豪华间(元/人/天)
贵宾间(元/人/天)
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了________人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;________
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
26.某产品生产车间有工人10名,已知每名工人每天可生产甲种产品10个或乙种产品12个,且每生产一个甲种产品可获得利润100元,每生产一个乙种产品可获得利润150元.在这10名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品.
(1)求出此车间每天获取利润y(元)与x(人)之间的函数关系式;
(2)若要使此车间每天获取利润为14800元,要派多少名工人去生产甲种产品?
(3)若要使此车间每天获取利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适?
27.在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900
,
且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。
28.为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动,自行车队从甲地出发,目的地为乙地,在自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地。自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的3倍,如图所示的是自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地的时间x(h)的关系图象,请根据图象提供的信息,回答下列问题:
(1)自行车队行驶的速度是________;邮政车行驶的速度是________;a=________。
(2)邮政车出发多少小时与自行车队相遇?
(3)当邮政车与自行车队相距15km时,此时离邮政车出发经过了多少小时?
答案解析部分
一、单选题
1.【答案】
D
解:(1)
y=x,是一次函数
;(2)
,是一次函数;(3)
,不是一次函数;(4)
,是一次函数;(5)s=12t,是一次函数;(6)y=30-4x,是一次函数,共5个.
故答案为:D.
【分析】直接利用一次函数的一般形式y=kx+b(k≠0)分析得出答案.
2.【答案】
D
解:∵一次函数y=(m+1)x+m2-1(m为常数)的图象过原点,
∴m2-1=0,解得m=±1.
∵此函数是一次函数,
∴m+1≠0,解得m≠-1,
∴m=1.
故答案为:D.
【分析】将(0,0)代入一次函数解析式中,可得m2-1=0,解得m=±1.根据一次函数的定义可知m≠-1,据此解答即可.
3.【答案】
A
解:A、由一次函数图象可知:
,
,则此时
,
由正比例函数图象可得:
,故该选项正确;
B、由一次函数图象可知:
,
,则此时
,
由正比例函数图象可得:
,互相矛盾,故该选项错误;
C、由一次函数图象可知:
,
,则此时
,
由正比例函数图象可得:
,互相矛盾,故该选项错误;
D、由一次函数图象可知:
,
,则此时
,
由正比例函数图象可得:
,互相矛盾,故该选项错误.
故答案为:A.
【分析】根据一次函数图象与系数的关系以及正比例函数图象与系数的关系逐一对各选项进行判断,然后进一步得出答案即可.
4.【答案】
A
解:A和B中,L0=10,表示弹簧短;A和C中,K=0.5,表示弹簧硬;
故答案为:A
【分析】A和B中,L0=10,表示弹簧短;A和C中,K=0.5,表示弹簧硬,由此即可得出结论.
5.【答案】
B
解:根据图象可求出直线
,
的解析式分别为:
,所以两直线的交点坐标可以看作方程组
的解,
故答案为:B.
【分析】通过观察图像得出l1,l2的k、b值,求出解析式,两个直线的交点就可以看作两个方程的解。
6.【答案】
C
解:∵直线y1=kx+b过点A(0,3)和点P(1,m),
∴0+b=3,k+b=m
∴b=3,k=m-3
∴(m-3)x+3>mx-2
mx-3x+3>mx-2
解之:
∵点P(1,m)
∴mx>kx+b>mx-2的解集为.
故答案为:C
【分析】由题意可知直线y1=kx+b过点A(0,3)和点P(1,m),将这两点代入函数解析式,可得到k=m-3,再将k的值代入不等式,可得到mx-3x+3>mx-2,解不等式可得到x的取值范围,再根据点P的横坐标,就可得到不等式组的解集。
7.【答案】
C
解:∵x=3时,及R从N到达点P时,面积开始不变,
∴PN=3,同理可得OP=5,
∴矩形的周长为2×(3+5)=16.
故选C.
8.【答案】
B
解:①以A为直角顶点,可过A作直线垂直于AB,与y轴交于一点,这一点符合点P的要求;
②以B为直角顶点,可过B作直线垂直于AB,与y轴交于一点,这一点也符合P点的要求;
③以P为直角顶点,与y轴共有2个交点.
所以满足条件的点P共有4个.
故选B.
【分析】当∠PBA=90°时,即点P的位置有2个;当∠ABP=90°时,点P的位置有1个;当∠BAP=90°时,在y轴上共有1个交点.
9.【答案】B
解:由题意得?
:
0<2m-1<m+2
①
;0<2m-1<-2m+4②?
;
解得?
:;
故应选?
B.
【分析】此题分两种情况①点P在x轴上方在直线l1右边;列出不等式0<2m-1<m+2,②点P在x轴上方在直线l2左边,列出不等式0<2m-1<-2m+4,解两不等式组成的不等式组,即可得出答案。
10.【答案】
C
解:摩托车比汽车晚到:4﹣3=1h,故①正确,
A、B两地的路程为20km,故②正确,
摩托车的速度为(180﹣20)÷4=40km/h,汽车的速度为180÷3=60km/h,故③错误,
设汽车出x小时与摩托车相遇,则60x=20+40x,得x=1,此时距离B地40×1=40km,故④正确,
故答案为:C
【分析】①中,根据汽车和摩托车用的时间,即可得到摩托车比汽车晚一个小时;
②中,根据时间为0时,二者的距离即为AB之间的距离;
③中,根据图象,分别求出摩托车和汽车的速度即可;
④中,当二者的路程一样时,为二者相遇的时间,继而求出与B地的距离即可。
11.【答案】
C
解:根据题意可以列出甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数关系得:
y甲=-15x+30
y乙=
由此可知,①②符合题意.
当15x+30=30x时,
解得x=
则M坐标为(
,20),故③符合题意.
当两人相遇前相距10km时,
30x+15x=30-10
x=
,
当两人相遇后,相距10km时,
30x+15x=30+10,
解得x=
15x-(30x-30)=10
解得x=
∴④不符合题意.
故答案为C.
【分析】根据题意,确定①-③符合题意,当两人相距10千米时,应有3种可能性.
12.【答案】
B
解:①甲的速度为
千米/小时,故符合题意;
②t≤1时,乙的速度为
千米/小时,t>1后,乙的速度为
千米/小时,故不符合题意;
③行驶1小时时,甲走了40千米,乙走了50千米,乙在甲前10千米处,故符合题意;
④∵甲的速度为40千米/小时:甲的函数表达式为:y=40x,
乙的函数表达为:0≤t≤1时,乙的速度为50千米/小时,∴y=50x,
t>1时,设y=kx+b,
将点(1,50),(3,120)代入得:
,解得k=35,b=15,
∴t>1时,y=35x+15,
t=0.5时,甲、乙两名运动员相距=50×
-40×
=5(千米),
t=2时,甲、乙两名运动员相距=(35×2+15)?2×40=5(千米),
同理t=4时,甲、乙两名运动员相距为5千米,故不符合题意.
故答案为:B.
【分析】①甲的速度为
千米/小时,即可求解;②t≤1时,乙的速度为50千米/小时,t>1后,乙的速度为
千米/小时,即可求解;③行驶1小时时,甲走了40千米,乙走了50千米,即可求解;④甲的函数表达式为:y=40x,乙的函数表达为:0≤t≤1时,y=50x,t>1时,y=35x+15,即可求解.
二、填空题
13.【答案】
-2
解:∵函数
是一次函数
∴
解得:m=-2
故答案为:-2.
【分析】根据一次函数的定义即可求出结论.
14.【答案】
解:将点P(m,3)代入直线y=x+2中,
得m+2=3,
∴m=1.
∴点P(1,3),
∴方程组??的解为?.
故答案为:
?.
【分析】将点P(m,3)代入直线y=x+2中,求出m的值,即得点P的坐标,点P的横纵坐标即是两直线解析式的相对应方程组的解.
15.【答案】
x>-3
解:∵函数y=-2x和y=kx+b的图象相交于点A(m,6),
∴6=-2m,
解得:m=-3,
故A点坐标为:(-3,6),
∵kx+b>-2x时,
∴(k+2)x+b>0,
则关于x的不等式(k+2)x+b>0的解集为:x>-3.
故答案为:x>-3.
【分析】直接利用函数图象上点的坐标特征得出m的值,再利用函数图象得出答案.
16.【答案】
解:把(
,
)代入y1=kx+1,可得
,
解得k=n-3,
代入不等式得nx-3<nx-3x+1<nx,
解得:
∴不等式组mx-2<kx+1<mx的解集为
。
故答案为:
。
【分析】根据一次函数的性质,将(
,
)代入y1=kx+1得k=n-3,将k=n-3,代入不等式组,求解即可得出该不等式的解集。
17.【答案】
解:如图,分别求出y1
,
y2
,
y3交点的坐标A(
,
);B(
,
);C(
,
)
当x<
,y=y1;
当
≤x<
,y=y2;
当
≤x<
,y=y2;
当x≥
,y=y3
.
∵y总取y1
,
y2
,
y3中的最小值,
∴y的取值为图中红线所描述的部分,
则y1
,
y2
,
y3中最小值的最大值为C点的纵坐标
,
∴y最大=
.
【分析】y始终取三个函数的最小值,y最大值即求三个函数的公共部分的最大值.
18.【答案】
(1)240
(2)(12,2400)
(3)s=240t
(4)李越;3
解:(1)由图象可得,李越骑车的速度为:2400÷10=240米/分钟,
故答案为:240;(2)由题意可得,10+2=12(分钟),
点B的坐标为(12,2400),
故答案为:(12,2400);(3)设李越从乙地骑往甲地时,s与t之间的函数表达式为:s=kt,
由题意得:2400=10k,得:k=240,
即李越从乙地骑往甲地时,s与t之间的函数表达式为:s=240t,
故答案为:s=240t;(4)由图象可知,李越先到达乙地,先到达:2400÷96-(10×2+2)=3(分钟),
故答案为:李越,3.
【分析】(1)由函数图象中的数据可以直接计算出李越骑车的速度;(2)根据题意和图象中点A的坐标可以直接写出点B的坐标;(3)根据函数图象中的数据和待定系数法,可得s与t的函数表达式;(4)根据函数图象可以得到谁先到达乙地,并求出先到几分钟.
19.【答案】
解:∵一次函数y=2x+5中,令x=0,则y=5,令y=0,则x=﹣
,
∴A(0,5),B(﹣
,0).
∵PE⊥y轴于点E,PF⊥x轴于点F,
∴四边形PEOF是矩形,且EF=OP,
∵O为定点,P在线段上AB运动,
∴当OP⊥AB时,OP取得最小值,此时EF最小,
∵A(0,5),点B坐标为(﹣
,0),
∴OA=5,O
B=
,
由勾股定理得:AB=
=
=
,
∴AB?OP=OA?OB,
∴OP=
=
=
.
故答案为:
.
【分析】在一次函数y=2x+5中,分别令x=0和y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,满足条件,由条件可证明△AOB∽△OPB,利用相似三角形的性质可求得OP的长,即可求得EF的最小值.
20.【答案】②③④
解:观察函数图象可得出:
①兔子出发的时间为40分,①错误;
②“龟兔再次赛跑”的路程为1000米,②正确;
③乌龟休息的时间为40﹣30=10(分钟),③正确;
④设y2=k2x+b2(k2≠0),在40≤x≤60时间段内y1=k1x+b1(k1≠0),
将(40,600)、(60,1000)代入y1=k1x+b1中,得:
,解得:
,
∴y1=20x﹣200(40≤x≤60).
同理可求出:y2=100x﹣4000(40≤x≤50).
令y1=y2
,
即20x﹣200=100x﹣4000,
解得:x=
,
∴y1=20x﹣200=20×
﹣200=750,
∴兔子在途中750米处追上乌龟,④正确.
故答案为:②③④.
【分析】①由兔子出发时的时间为40分可得出①错误;②观察函数图象即可得出“龟兔再次赛跑”的路程为1000米,即②正确;③用40﹣30即可得出乌龟在途中休息了10分钟,即③正确;④设y2=k2x+b2(k2≠0),在40≤x≤60时间段内y1=k1x+b1(k1≠0),观察函数图象找出点的坐标利用待定系数法即可求出两函数关系式,令y1=y2求出x值,再将其代入y1中即可得出兔子在途中750米处追上乌龟,即④正确.综上即可得出结论.
三、解答题
21.
解:(1)∵点A的横坐标为3,且△AOH的面积为3
∴点A的纵坐标为﹣2,点A的坐标为(3,﹣2),
∵正比例函数y=kx经过点A,
∴3k=﹣2解得k=-,
∴正比例函数的解析式是y=-x;
(2)∵△AOP的面积为5,点A的坐标为(3,﹣2),
∴OP=5,
∴点P的坐标为(5,0)或(﹣5,0).
【分析】(1)根据题意求得点A的坐标,然后利用待定系数法求得正比例函数的解析式;
(2)利用三角形的面积公式求得OP=5,然后根据坐标与图形的性质求得点P的坐标
22.
解:(1)依题意得:学校离王老师家有10千米,从出发到学校王老师用了25分钟;
(2)依题意得:王老师吃早餐用了10分钟;
(3)吃早餐以前的速度为:5÷10=0.5km/分钟,吃完早餐以后的速度为:(10﹣5)÷(25﹣20)=1km/分钟=60km/小时,
∴王老师吃完早餐以后速度快,最快时速达到60km/小时.
【分析】(1)由于骑摩托车前往学校,途中在路旁一家饭店吃早餐,那么行驶路程s(千米)与时间t(分)之间的关系图象中有一段平行x轴的线段,然后学校,根据图象可以直接得到结论;
(2)根据图象中平行x轴的线段即可确定王老师吃早餐用了多少时间;
(3)根据图象可以分别求出吃早餐以前的速度和吃完早餐以后的速度,然后比较即可得到结果.
23.
解:
(1)∵
,
∴
可设OC=x,则OA=2x,
在Rt△AOC中,由勾股定理可得OC2+OA2=AC2
,
∴x2+(2x)2=(4
)2
,
解得x=4或x=-4(不合题意,舍去),
∴OC=4,OA=8,
∴A(8,0),C(0,4),
设直线AC解析式为y=kx+b,
∴
,
解得:
,
∴直线AC解析式为y=
x+4
(2)由折叠的性质可知AE=CE,
设AE=CE=y,则OE=8-y,
在Rt△OCE中,由勾股定理可得OE2+OC2=CE2
,
∴(8-y)2+42=y2
,
解得y=5,
∴AE=CE=5,
∵∠AEF=∠CEF,∠CFE=∠AEF,
∴∠CFE=∠CEF,
∴CE=CF=5,
∴S△CEF=
CF?OC=
×5×4=10,
即重叠部分的面积为10;
(3)由(2)可知OE=3,CF=5,
∴E(3,0),F(5,4),
设直线EF的解析式为y=k′x+b′,
∴
,
解得:
?,
∴直线EF的解析式为y=2x-6
【分析】
(1)设OC=x,则OA=2x,在Rt△OCE中,在Rt△AOC中,利用勾股定理可得OC2+OA2=AC2
,
求得A(8,0),C(0,4),然后用待定系数法确定直线的解析式。
(2)由折叠的性质可知AE=CE,在Rt△OCE中,由勾股定理可得OE2+OC2=CE2
,
解得AE=CE=5:再利用BC//OA,得到∠CFE=∠CEF,所以CE=CF=5,然后根据三角形的面积公式计算S△CEF
(3)首先求出E、F两点的坐标,然后利用待定系数法求出直线EF所在的解析式。
24.
解:(1)当x≥0时,y=|x|=x,即y=x(x≥0),将x=0代入得:y=0;将x=1代入得:y=1,
当x≤0时,y=|x|=﹣x,即y=﹣x(x≤0),将x=0代入得:y=0;将x=﹣1代入得:y=1.
过点O(0,0),A(﹣1,1)作射线OA,过点0(0,0),B(1,1)作射线OB,
函数y=|x|的图象如图所示:
(2)∵y=mx﹣2(m﹣1)=m(x﹣2)+2,
∴x﹣2=0,y=2
∴x=2,y=2,
即函数图象过定点(2,2)
(3)如下图:
∵函数y=mx﹣2(m﹣1)的图象经过顶点(2,2)
∴OC==2.
∴OD?OC=2,
∴OD=,
所以点D的坐标为(﹣1,1).
将x=﹣1,y=1代入y=mx﹣2(m﹣1)得:m=.
【分析】(1)将函数y=|x|,变形为y=x(x≥0),y=﹣x(x≤0),然后利用两点法画出函数图象即可;
(2)将函数解析式变形为:y=(x﹣2)+2,从而可知直线经过点(2,2);
(3)首先由勾股定理求得OC的长,然后根据三角形的面积为2,可求得OD的长度,从而可得到点D的坐标,将点D的坐标代入函数解析式可求得m的值.
四、综合题
25.
解:(1)设三人间普通客房住了x间,双人间普通客房住了y间.根据题意得:
????
解得:
∴三人间普通客房住了8间,双人间普通客房住了13间
(2);根据题意得:
?
即
?。
(3)不是,由上述一次函数可知,y随x的增大而减小,当三人间住的人数大于24人时,所需费用将少于1510元
【分析】(1)根据题意找出相等的关系量,由共有50人的旅游团,三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元,得到方程组,求出三人间普通客房和双人间普通客房住的间数;(2)由三人间共住了x人,则双人间住了(
50
?
x
)人,根据题意得到得到等式y
=
25
x
+
35
(
50
?
x
);(3)由上述一次函数可知,y随x的增大而减小,当三人间住的人数大于24人时,所需费用将少于1510元.
26.
解:(1)设每天安排x名工人生产甲种产品,则有(10-x)人生产乙产品,
y=10x×100+12(10-x)×150=-800x+18000,
答:每天获取利润y(元)与x(人)之间的函数关系式为y=-800x+18000;
(2)当y=14800时,即:-800x+18000=14800,
解得:x=4,
答:安排4人生产甲产品;
(3)由题意得:
-800x+18000≥15600,
解得:x≤3,
当x≤3时,10-x≥7,
因此至少要派7名工人生产乙产品.
【分析】(1)根据利润计算方法分别表示出甲产品、乙产品的利润,最后求和即得y,(2)把y=14800代入y与x的函数关系式,求出x的值,(3)列不等式求出x的取值范围,进而求出生产乙产品的人数的取值范围,确定至少安排乙产品的人数.
27.(1)证明:∵△ABC是等腰直角三角形
∴∠ACB=900
,
AC=BC
∴∠ACO+∠BCE=900
BE⊥CE,∴∠BCE+∠CBE=900
∴∠ACO=∠CBE
∴△AOC≌△CEB
(2)解:∵△AOC≌△CEB
∴BE=OC=2,CE=OA=4
∴点B的坐标为(6,2)
又一次函数y=x+b经过点B(6,2)
∴2=6+b
∴b=-4
∴点D的坐标为(0,-4)
∴
在△ABD中,AD边上高的长度就是B点纵坐标的绝对值.
∴S△ABD=
×8×6=24
∴△ABD的面积为24
【分析】(1)由等腰直角三角形的性质可证得AC=BC,∠ACO=∠CBE,进而可证得△AOC≌△CEB;(2)由(1)的全等,可得B坐标,代入解析式,可求出b,进而求出D坐标,AD的长,AD边上高的长度就是B点纵坐标,进而求出面积.
28.解:(1)自行车的速度==20km/h,
邮政车的速度=20×3=60km/h,
a=+1=.
故答案为:20km/h,60km/h,.
(2)设邮政车出发x小时两车相遇,分两种情况:①首次相遇,由题意得20(x+1)=60x,解得x=
故邮政车出发
小时两车首次相遇
②邮政车在返程途中与自行车队再次相遇.
根据题意得20(x+1)+60x=140×2,解得x=
故邮政车出发
小时后,在返程途中与自行车队再次相遇
即邮政车出发后
小时或
小时与自行车队相遇.
(3)设离邮政车出发经过了m小时与自行车队相距15km
当m<
时,①当自行车队在邮政车前面时,20(m+1)-60m=15,解得m=
②当邮政车在自行车队前面时,60m-20(m+1)=15,解得m=
当m>
时,①邮政车从乙地返回,与自行车队未相遇,20(m+1)+60m-140=140-15,解得m=
②邮政车从乙地返回,与自行车队相遇后,20(m+1)+60m-140=140+15,解得m=
即邮政车与自行车队相距15km时,此时离邮政车出发经过了
小时或
小时或
小时或
小时。
【分析】(1)由图象可得,全程为140km,
自行车行驶全程用7小时,代入速度公式即可求值,于是邮政车的速度可求,走完全程的时间也可求,看图可知a值等于邮政车走完全程的时间再加1小时.
(2)
设邮政车出发x小时两车相遇,
分两种情况:①首次相遇,
邮政车行驶的路程为60x,
自行车行驶的路程为20(x+1),据此列方程求解即可;
②邮政车在返程途中与自行车队再次相遇,这时两者的路程之和正好等于全程的2倍,据此列方程即可求解.
(3)分两种情况讨论,其中每种情况又下分两种情况讨论,
设离邮政车出发经过了m小时与自行车队相距15km,则邮政车行驶的路程为60m,自行车行驶的路程为
20(m+1),?当邮政车在去乙地的途中分两种情况,
当自行车队在邮政车前面时,?可得20(m+1)-60m=15;当邮政车在自行车前面时,可得?60m-20(m+1)=15;当邮政车在返回的途中也分两种情况,
①邮政车从乙地返回,与自行车队未相遇,可得20(m+1)+60m-140=140-15,
?②邮政车从乙地返回,与自行车队相遇后,可得20(m+1)+60m-140=140+15,
分别列式求解即可.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
