冀教版数学八上14.3.2实数的性质及分类课件(图片版、16张ppt)
文档属性
| 名称 | 冀教版数学八上14.3.2实数的性质及分类课件(图片版、16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-01 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
14.3.2实数的性质及分类
第十四章
实数
1你还记得有理数的分类吗?
有理数/整数有理数0
正有理数
1分数
负有理数
2分类的基本原则是什么?
分类的基本原则:不重不漏
一实数与数轴上的点
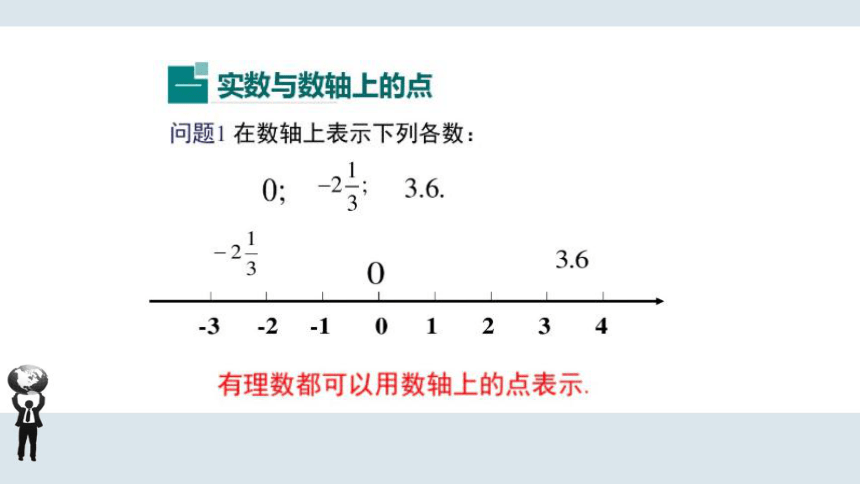
问题1在数轴上表示下列各数:
2
3.6
3-2-101234
有理数都可以用数轴上的点表示
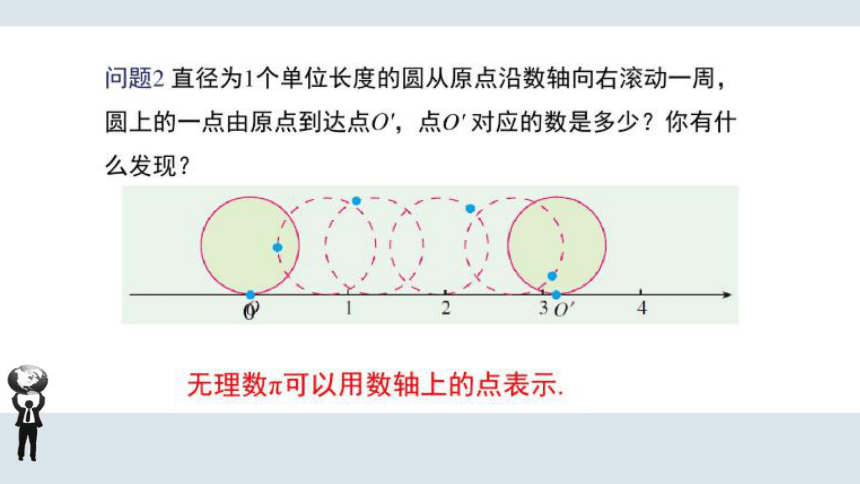
问题2直径为1个单位长度的圆从原点沿数轴向右滚动一周,
圆上的一点由原点到达点O,点O'对应的数是多少?你有什
么发现?
30
无理数π可以用数轴上的点表示
◆实数与数轴上的点
1每一个有理数都可以用数轴上的点表示;
2每一个无理数都可以用数轴上的点表示
3实数与数轴上的点是一一对应的
二实数的倒数、相反数及绝对值
在实数范围内,相反数、倒数、绝对值的意义,和有理数范
围内的相反数、倒数、绝对值的意义完全一样.
(1)实数的相反数是a;
(2)实数a(a0)的倒数是1;
(3)正数的绝对值是它本身,一个负数的绝对值是
它的相反数,0的绝对值是0
国实数的分类
问题你能对我们学过的数进行合理的分类吗?
解
实数/有理数
正实数正有理数
正无理数
无理数’实数{0
负实数负有理数
负无理数
◆实数的分类
有理数
正有理数
实数(有限小数或{零
无限循环小数)(负有理数
无理数
正无理数
(无限不循环小数)负无理数
整数
或有理数
分数
有限小数及无限循环小数
正整数
整数
0自然数
实/有理
负整数
数
分数厂正分数
负分数
无理数正无理数
负无理数
无限不循环小数
例把下列各数填入相应的集合内
4.
27,0.15.-7.5,-兀
V173
(1)有理数集合:
(2)无理数集合:
(3)正实数集合:
(4)负实数集合
4.2,-270.15.-75…}
3
一T
5,4,
0.15
V173
√-27,-7.5,-π
提示)不是带根号的都是无理数
当堂练习
1.判断:
(1)实数不是有理数就是无理数
(2)无理数都是无限不循环小数
(3)无理数都是无限小数
(4)带根号的数都是无理数
(5)无理数一定都带根号.
(6)两个无理数之积不一定是无理数
(7)两个无理数之和一定是无理数
(8)数轴上的任何一点都可以表示实数
2两个实数在数轴上的对应点和原点的距离相等,则这两个
数()
A.一定相等
B.一定不相等
C相等或互为相反数
D以上都不对
3下列各组数中,互为相反数的是()
A.-3与
B|-3与
C|-3与1
D.-3与3
14.3.2实数的性质及分类
第十四章
实数
1你还记得有理数的分类吗?
有理数/整数有理数0
正有理数
1分数
负有理数
2分类的基本原则是什么?
分类的基本原则:不重不漏
一实数与数轴上的点
问题1在数轴上表示下列各数:
2
3.6
3-2-101234
有理数都可以用数轴上的点表示
问题2直径为1个单位长度的圆从原点沿数轴向右滚动一周,
圆上的一点由原点到达点O,点O'对应的数是多少?你有什
么发现?
30
无理数π可以用数轴上的点表示
◆实数与数轴上的点
1每一个有理数都可以用数轴上的点表示;
2每一个无理数都可以用数轴上的点表示
3实数与数轴上的点是一一对应的
二实数的倒数、相反数及绝对值
在实数范围内,相反数、倒数、绝对值的意义,和有理数范
围内的相反数、倒数、绝对值的意义完全一样.
(1)实数的相反数是a;
(2)实数a(a0)的倒数是1;
(3)正数的绝对值是它本身,一个负数的绝对值是
它的相反数,0的绝对值是0
国实数的分类
问题你能对我们学过的数进行合理的分类吗?
解
实数/有理数
正实数正有理数
正无理数
无理数’实数{0
负实数负有理数
负无理数
◆实数的分类
有理数
正有理数
实数(有限小数或{零
无限循环小数)(负有理数
无理数
正无理数
(无限不循环小数)负无理数
整数
或有理数
分数
有限小数及无限循环小数
正整数
整数
0自然数
实/有理
负整数
数
分数厂正分数
负分数
无理数正无理数
负无理数
无限不循环小数
例把下列各数填入相应的集合内
4.
27,0.15.-7.5,-兀
V173
(1)有理数集合:
(2)无理数集合:
(3)正实数集合:
(4)负实数集合
4.2,-270.15.-75…}
3
一T
5,4,
0.15
V173
√-27,-7.5,-π
提示)不是带根号的都是无理数
当堂练习
1.判断:
(1)实数不是有理数就是无理数
(2)无理数都是无限不循环小数
(3)无理数都是无限小数
(4)带根号的数都是无理数
(5)无理数一定都带根号.
(6)两个无理数之积不一定是无理数
(7)两个无理数之和一定是无理数
(8)数轴上的任何一点都可以表示实数
2两个实数在数轴上的对应点和原点的距离相等,则这两个
数()
A.一定相等
B.一定不相等
C相等或互为相反数
D以上都不对
3下列各组数中,互为相反数的是()
A.-3与
B|-3与
C|-3与1
D.-3与3
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
