人教版七年级数学上册 程 3.4实际问题与一元一次方程(第四课时)(共37张PPT)
文档属性
| 名称 | 人教版七年级数学上册 程 3.4实际问题与一元一次方程(第四课时)(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 277.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-01 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
第三章
一元一次方程
3.4实际问题与一元一次方程
第四课时
【学习目标】
1.能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案
2.能用方程模型解决较为复杂的综合问题
3.体会分类思想、建模思想和方程思想,增强应用数学意识和应用能力.
【课前预习】
1.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为(
)
A.购买A类会员年卡
B.购买B类会员年卡
C.购买C类会员年卡
D.不购买会员年卡
2.甲队有工人272人,乙队有工人196人,如果要求乙队的人数是甲队人数的,应从乙队调多少人去甲队.如果设应从乙队调x人到甲队,列出的方程正确的是( )
3.某商店进了一批商品,每件商品的进价为a元,若想获利20%,则每件商品的零售价定为
4.在一个笼子里面放着几只鸡与几只兔,数了数一共有14个头,44只脚.问鸡兔各有几只设鸡为x只,得方程( )
A.2x+4(14﹣x)=44
B.4x+2(14﹣x)=44
C.4x+2(x﹣14)=44
D.2x+4(x﹣14)=44
5.若关于的方程是一元一次方程,则这个方程的解是(
)
会员年卡类型
办卡费用(元)
每次游泳收费(元)
A类
50
25
B类
200
20
C类
400
15
【课前预习】答案
1.C
2.C
3.D
4.A
5.A
【学习探究】
思考
某市出租车的收费标准为:起步价10元,3千米后每千米1.2元,某人乘出租车花了14.8元,他乘车行驶了多少千米?
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/min)
主叫限定时间/min
月使用
费/元
下面是手机卡的两种计费方式,请你计算一下哪种方式更省钱.
(1)设一个月内用移动电话主叫为t
min(t为正整数).根据上表,列表说明:当在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
考虑下列问题:
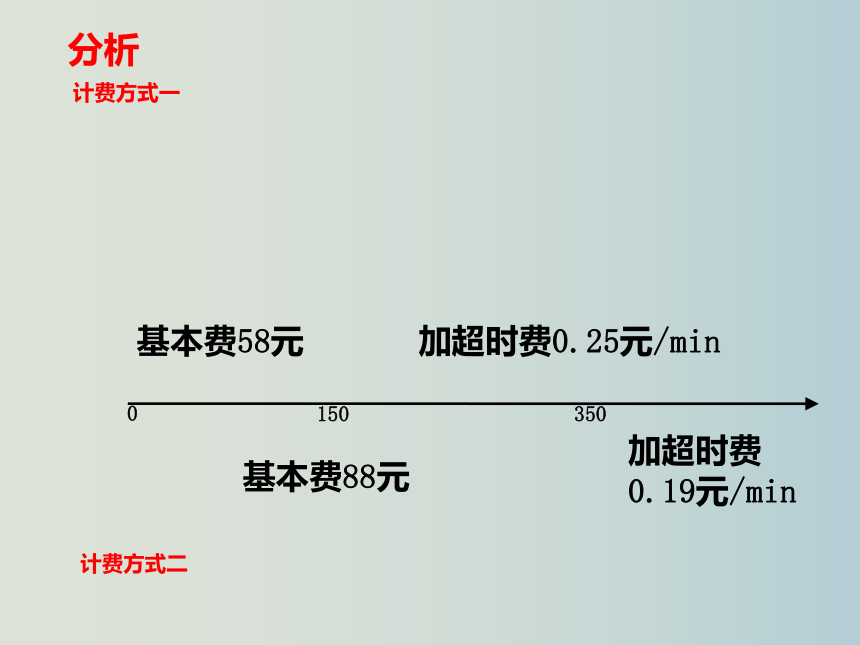
分析
加超时费0.19元/min
基本费88元
加超时费0.25元/min
基本费58元
计费方式一
计费方式二
350
0
150
设一个月内用移动电话主叫为t
分(t是正整数).根据表1,当
t
在不同时间范围内取值,列表说明按方式一和方式二如何计费.
主叫时间t
/分
方式一计费/元
方式二计费/元
t
小于150
t
等于150
t
大于150且小于
350
t
等于350
t
大于350
营业厅根据________的不同进行收费,所以我们可以根据主叫限定时间进行分情况讨论,把____和____作为不同时间范围的划分点,可以分为几种情况:
主叫时间
150
350
(1)t<150
(2)t=150
(3)150<t<350
(4)t=350
(5)t>350
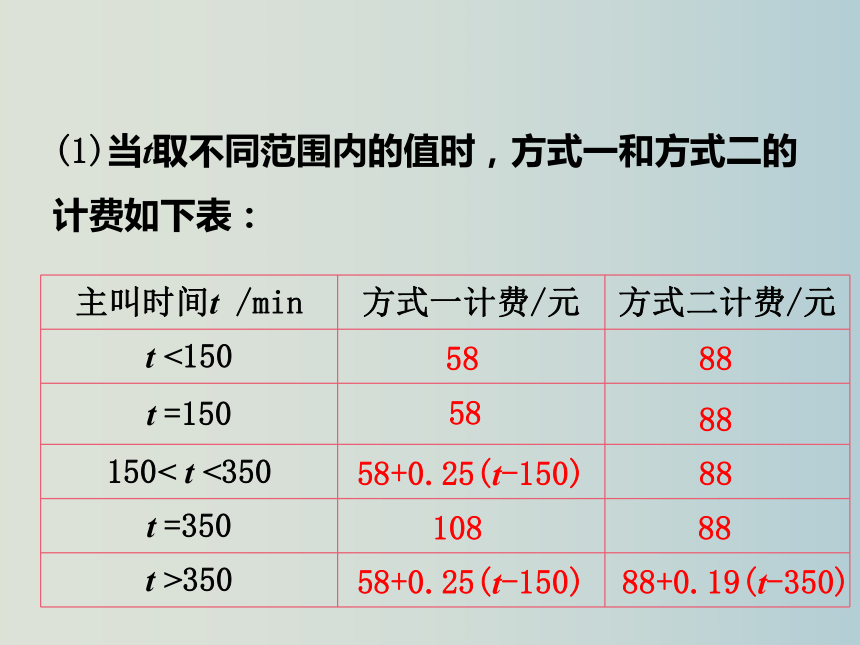
(1)当t取不同范围内的值时,方式一和方式二的计费如下表:
主叫时间t
/min
方式一计费/元
方式二计费/元
t
<150
t
=150
150<
t
<350
t
=350
t
>350
58
58
58+0.25(t-150)
108
58+0.25(t-150)
88
88
88
88
88+0.19(t-350)
主叫时间t
/分
方式一计费/元
方式二计费/元
t
小于150
58
88
t
等于150
58
88
t
大于150且小于
350
58+0.25(t-150)
88
t
等于350
108
88
t
大于350
58+0.25(t-150)
88+0.19(t-350)
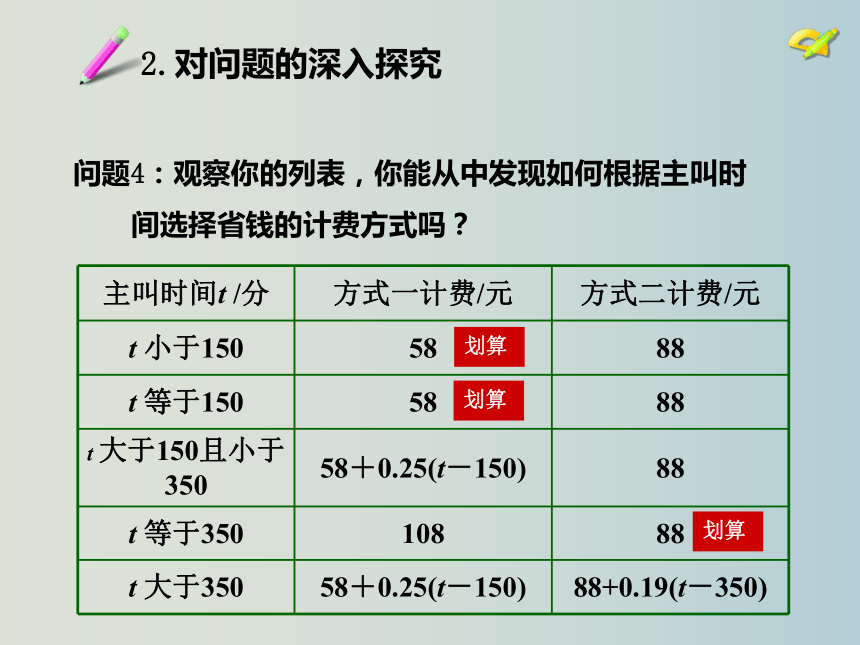
2.对问题的深入探究
问题4:观察你的列表,你能从中发现如何根据主叫时
间选择省钱的计费方式吗?
划算
划算
划算
(2)观察上表,可以看出:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.
①从表格中,可以看出当t≤150时,按方式一的计费少.
②当t从150增加到350时,按方式一的计费由58元增加到108元,而方式二的计费一直是88元,所以方式一在变化过程中,可能在某一主叫时间,两种方式计费相等.
列方程58+0.25(t-150)=88.
解得t=270.
故当
t
=270时,两种计费方式的费用相同,都是88元;当150当270350时,按方式一计费多于按方式二计费.
③当t
=350时,按方式二的计费少.
④当t>350时,可以看出,按方式一的计费
为108元加上超过350
min部分的超时费0.25
×(t
-350)元,按方式二的计费为88元加上超过350
min部分的超时费0.19(t-350)元,故按方式二的计费少.
加超时费0.19元/min
基本费88元
加超时费0.25元/min
基本费58元
350
0
150
(
t
是正整数)
t
/min
270
计费方式一
计费方式二
当t<270
min时,选择方案一省钱;
当t>270
min时,选择方案二省钱;
当t=270
min时,选择方案一和方案二一样.
根据以上分析,可以发现
小结
请回顾电话计费问题的探究过程,并回答
以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法,你有
哪些收获?
某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价40元,乒乓球每盒10元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需买球拍6副,乒乓球若干盒(不小于6盒).
例题
(1)当购买多少盒乒乓球时,两种优惠办法
付款一样?
(2)当购买20盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?
(3)当购买40盒乒乓球时,请你去办这件事,
你打算去哪家商店购买?为什么?
解:(1)设当购买乒乓球x盒时,两种优惠办法付款一样.根据题意,得
40
×
6+10(x
-6)=(40×6+10x)×90%.
解得x=36.
答:当购买36盒乒乓球时,两种优惠办法付款一样.
(2)当购买20盒乒乓球时,
去甲商店需付款:
40×6+10×
(20-6)=380(元)
去乙商店需付款:
(40×6+10×20)
×90%=396(元)
因为380元<396元,所以当购买20盒乒乓球时,
去甲商店购买划算.
(3)当购买40盒乒乓球时,
去甲商店需付款:
40
×
6+10(40-6)=
580(元)
去乙商店需付款:
(40×6+10×40)×90%=576(元)
因为576元<580元,所以当购买40盒乒乓球时,
去乙商店购买划算.
两种移动电话计费方式表
全球通
神州行
月租费
50元/月
0
本地通话费
0.40元/分
0.60元/分
(1)一个月内在本地通话200分和300分,按两种计费方式各须交费多少元?
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗?
怎么计算交费
交费=月租费+当月通话时间×单价(元/分)
【例题】
全球通
神州行
200分
300分
解:(1)
(2)设累计通话t分钟,则用“全球通”要收费(50+0.4t)元,用“神州行”要收费0.6t。如果两种收费一样,则
0.6t=50+0.4t解此方程得:
0.2t=50.
所以
t=250.
答:如果一个月内通话250分,那么两种计费方式的收费相同.
130元
120元
170元
180元
问题:什么情况下用“全球通”优惠一些?什么情况下用“神州行”优惠一些?
小明想在两种灯中选购一种,其中一种是11瓦(即0.011千瓦)
的节能灯,售价60元;另一种是60瓦(即0.06千瓦)的白炽灯,
售价3元.两种灯的照明效果一样,使用寿命也相同(3
000小
时以上).节能灯售价较高,但是较省电;白炽灯售价低,但是
用电多.如果电费是0.5元/(千瓦时),选哪种灯可以节省费用(灯的售价加电费)?
分析:问题中有以下基本等量关系:
费用=灯的售价+电费;
电费=0.5×灯的功率(千瓦)
×照明时间(时).
【跟踪训练】
(1)设照明时间为t小时,则
总费用
售价
电费
节能灯
60元
白炽灯
3元
(2)用特殊值试探:如果取
t=2
000时,
节能灯的总费用为:60+0.5×0.011t
=60+0.5×0.011×2
000=71;
白炽灯的总费用为:3+0.5×0.06t
=3+0.5×0.06×2
000=63;
60+0.5×0.011t
3+0.5×0.06t
0.5×0.011t
0.5×0.06t
由两组数值可以说明,照明
时间不同,为了省钱而选择
用哪种灯的答案也不同.
如果取t=2
500呢?
请你算一算节能灯与白炽灯哪个费用较低?
解:设照明时间为t小时,
则节能灯的总费用为(60+0.5×0.011t)元;
白炽灯的总费用为(3+0.5×0.06t)元;
如果两个总费用相等,则有
60+0.5×0.011t
=3+0.5×0.06t
解此方程得:t≈2
327(小时)
因此我们可以取t=2
000小时和t=2
500小时,分别计算节能灯和白炽灯的总费用.
当t=2000时,
节能灯的总费用为:
60+0.5×0.011t
=60+0.5×0.011×2
000=71;
白炽灯的总费用为:
3+0.5×0.06t
=3+0.5×0.06×2
000=63;
当t=2500时,
节能灯的总费用为:60+0.5×0.011×2
500=73.75;
白炽灯的总费用为:3+0.5×0.06×2
500=78;
因此由方程的解和试算判断:
在t<2
327小时时,选择白炽灯优惠一些;
在t≈2
327小时时,两种灯的总费用一样;
在t>2
327小时而不超过使用寿命时,选择节能灯优惠一些.
小明想在两种灯中选购一种,其中一种是11瓦(即0.011千
瓦)的节能灯,售价60元;另一种是60瓦(即0.06千瓦)的白
炽灯,售价3元.两种灯的照明效果一样,使用寿命也相同
(3000小时以上).节能灯售价较高,但是较省电;白炽灯售
价低,但是用电多.如果电费是0.5元/(千瓦时),选哪种灯
可以节省费用(灯的售价加电费)?
问题:
如果灯的使用寿命都是3
000小时,而计划照明3
500
小时,则需要购买两个灯,试设计你认为能省钱的选灯方案.
参考方案:买白炽灯和节能灯各一只,用白炽灯照明500小时,
节能灯照明3
000小时.
在这种方案中的总费用为:
60+0.5×0.011×3
000+3+0.5×0.06×500
=60+16.5+3+15
=94.5(元).
你的方案的总费用是多少?
小结:
(1)解决这种问题的关键是什么?
(2)解决这种问题的步骤是什么?
找分界点,确定相等关系
观察,分析,判断,解答,验证
【课后练习】
1.某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电量15万度.如果设上半年每月平均用电x度,则所列方程正确的是(
)
A.6x+6(x-2000)=150000
B.6x+6(x+2000)=150000
C.6x+6(x-2000)=15
D.6x+6(x+2000)=15
2.某班分两组去两处植树,第一组22人,第二组26人.现第一组在植树中遇到困难,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A.22+x=2×26
B.22+x=2(26﹣x)
C.2(22+x)=26﹣x
D.22=2(26﹣x)
3.小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
A.x+5(12﹣x)=48
B.x+5(x﹣12)=48
C.x+12(x﹣5)=48
D.5x+(12﹣x)=48
4.某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地占林地面积的20%,设把x公顷旱地改为林地,则可列方程(
)
A.54?x=20%×108
B.54?x=20%×(108+x
C.54+x=20%×162
D.108?x=20%(54+x)
5.一船在静水中的速度为,水流速度为,从甲码头顺流航行到乙码头,再返回甲码头共用若设甲、乙两码头的距离为xkm,则下列方程正确的是
6.甲、乙两工程队开挖一条水渠各需10天、15天,两队合作2天后,甲有其他任务,剩下的工作由乙队单独做,还需多少天能完成任务?设还需x天,可得方程( )
7.小刚从家跑步到学校,每小时跑12km,会迟到5分钟;若骑自行车,每小时骑15km,则可早到10分钟.设他家到学校的路程是xkm,则根据题意列出方程是( )
8.一项工程,甲独做需10天完成,乙单独做需15天完成,两人合作4天后,剩下的部分由乙独做全部完成,设乙独做x天,由题意得方程( )
9.商店对某种手机的售价作了调整,按原售价的
8
折出售,此时的利润率为
14%,若此种手机的进价为
1200
元,设该手机的原售价为
x
元,则下列方程正确的是(
)
A.0.8x﹣1200=1200×14%
B.0.8x﹣1200=14%x
C.x﹣0.8x=1200×14%
D.0.8x﹣1200=14%×0.8x
10.一游泳池计划注入一定体积的水,按每小时500立方米的速度注水,注水2小时,注水口发生故障,停止注水,经20分钟抢修后,注水速度比原来提高了,结果比预定的时间提前了10分钟完成注水任务,则计划注入水的体积为
11.有一位工人师傅要锻造底面直径为40cm的“矮胖”形圆柱,可他手上只有底面直径是10cm、高为80cm的“瘦长”形圆柱,若不计损耗,则锻造出的“矮胖”形圆柱的高为________.
12.一艘船从甲码头到乙码头顺流行驶,用了2个小时,从乙码头返回甲码头逆流行驶,用了2.5小时,已知水流的速度是3千米/时,则船在静水中的速度是_____千米/时.
13.张老师带学生乘车外出郊游,甲车主说:”不论师生,每人8折,"乙车主说:“学生9折,老师免费,“张老师算了一下,不论坐谁的车,费用一样,则张老师带的学生人数是________.
14.湖园中学学生志愿服务小组在“三月学雷锋”活动中,购买了一批牛奶到敬老院慰问老人,如果送给每位老人2盒牛奶,那么剩下16盒;如果送给每位老人3盒牛奶,则正好送完.设敬老院有x位老人,依题意可列方程为
.
15.一个两位数,个位上的数字是十位上数字的3倍,它们的和是12,那么这个两位数是____.
【课后练习】答案
1.A
2.B
3.A
4.B
5.D
6.A
7.D
8.B
9.A
10.B
11.5cm
12.27
13.8人
14.2x+16=3x.
15.39
第三章
一元一次方程
3.4实际问题与一元一次方程
第四课时
【学习目标】
1.能够根据已知条件选择分类关键点对“电话计费问题”进行整体分析,从而得出整体选择方案
2.能用方程模型解决较为复杂的综合问题
3.体会分类思想、建模思想和方程思想,增强应用数学意识和应用能力.
【课前预习】
1.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为(
)
A.购买A类会员年卡
B.购买B类会员年卡
C.购买C类会员年卡
D.不购买会员年卡
2.甲队有工人272人,乙队有工人196人,如果要求乙队的人数是甲队人数的,应从乙队调多少人去甲队.如果设应从乙队调x人到甲队,列出的方程正确的是( )
3.某商店进了一批商品,每件商品的进价为a元,若想获利20%,则每件商品的零售价定为
4.在一个笼子里面放着几只鸡与几只兔,数了数一共有14个头,44只脚.问鸡兔各有几只设鸡为x只,得方程( )
A.2x+4(14﹣x)=44
B.4x+2(14﹣x)=44
C.4x+2(x﹣14)=44
D.2x+4(x﹣14)=44
5.若关于的方程是一元一次方程,则这个方程的解是(
)
会员年卡类型
办卡费用(元)
每次游泳收费(元)
A类
50
25
B类
200
20
C类
400
15
【课前预习】答案
1.C
2.C
3.D
4.A
5.A
【学习探究】
思考
某市出租车的收费标准为:起步价10元,3千米后每千米1.2元,某人乘出租车花了14.8元,他乘车行驶了多少千米?
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/min)
主叫限定时间/min
月使用
费/元
下面是手机卡的两种计费方式,请你计算一下哪种方式更省钱.
(1)设一个月内用移动电话主叫为t
min(t为正整数).根据上表,列表说明:当在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
考虑下列问题:
分析
加超时费0.19元/min
基本费88元
加超时费0.25元/min
基本费58元
计费方式一
计费方式二
350
0
150
设一个月内用移动电话主叫为t
分(t是正整数).根据表1,当
t
在不同时间范围内取值,列表说明按方式一和方式二如何计费.
主叫时间t
/分
方式一计费/元
方式二计费/元
t
小于150
t
等于150
t
大于150且小于
350
t
等于350
t
大于350
营业厅根据________的不同进行收费,所以我们可以根据主叫限定时间进行分情况讨论,把____和____作为不同时间范围的划分点,可以分为几种情况:
主叫时间
150
350
(1)t<150
(2)t=150
(3)150<t<350
(4)t=350
(5)t>350
(1)当t取不同范围内的值时,方式一和方式二的计费如下表:
主叫时间t
/min
方式一计费/元
方式二计费/元
t
<150
t
=150
150<
t
<350
t
=350
t
>350
58
58
58+0.25(t-150)
108
58+0.25(t-150)
88
88
88
88
88+0.19(t-350)
主叫时间t
/分
方式一计费/元
方式二计费/元
t
小于150
58
88
t
等于150
58
88
t
大于150且小于
350
58+0.25(t-150)
88
t
等于350
108
88
t
大于350
58+0.25(t-150)
88+0.19(t-350)
2.对问题的深入探究
问题4:观察你的列表,你能从中发现如何根据主叫时
间选择省钱的计费方式吗?
划算
划算
划算
(2)观察上表,可以看出:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.
①从表格中,可以看出当t≤150时,按方式一的计费少.
②当t从150增加到350时,按方式一的计费由58元增加到108元,而方式二的计费一直是88元,所以方式一在变化过程中,可能在某一主叫时间,两种方式计费相等.
列方程58+0.25(t-150)=88.
解得t=270.
故当
t
=270时,两种计费方式的费用相同,都是88元;当150
③当t
=350时,按方式二的计费少.
④当t>350时,可以看出,按方式一的计费
为108元加上超过350
min部分的超时费0.25
×(t
-350)元,按方式二的计费为88元加上超过350
min部分的超时费0.19(t-350)元,故按方式二的计费少.
加超时费0.19元/min
基本费88元
加超时费0.25元/min
基本费58元
350
0
150
(
t
是正整数)
t
/min
270
计费方式一
计费方式二
当t<270
min时,选择方案一省钱;
当t>270
min时,选择方案二省钱;
当t=270
min时,选择方案一和方案二一样.
根据以上分析,可以发现
小结
请回顾电话计费问题的探究过程,并回答
以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法,你有
哪些收获?
某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价40元,乒乓球每盒10元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需买球拍6副,乒乓球若干盒(不小于6盒).
例题
(1)当购买多少盒乒乓球时,两种优惠办法
付款一样?
(2)当购买20盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?
(3)当购买40盒乒乓球时,请你去办这件事,
你打算去哪家商店购买?为什么?
解:(1)设当购买乒乓球x盒时,两种优惠办法付款一样.根据题意,得
40
×
6+10(x
-6)=(40×6+10x)×90%.
解得x=36.
答:当购买36盒乒乓球时,两种优惠办法付款一样.
(2)当购买20盒乒乓球时,
去甲商店需付款:
40×6+10×
(20-6)=380(元)
去乙商店需付款:
(40×6+10×20)
×90%=396(元)
因为380元<396元,所以当购买20盒乒乓球时,
去甲商店购买划算.
(3)当购买40盒乒乓球时,
去甲商店需付款:
40
×
6+10(40-6)=
580(元)
去乙商店需付款:
(40×6+10×40)×90%=576(元)
因为576元<580元,所以当购买40盒乒乓球时,
去乙商店购买划算.
两种移动电话计费方式表
全球通
神州行
月租费
50元/月
0
本地通话费
0.40元/分
0.60元/分
(1)一个月内在本地通话200分和300分,按两种计费方式各须交费多少元?
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗?
怎么计算交费
交费=月租费+当月通话时间×单价(元/分)
【例题】
全球通
神州行
200分
300分
解:(1)
(2)设累计通话t分钟,则用“全球通”要收费(50+0.4t)元,用“神州行”要收费0.6t。如果两种收费一样,则
0.6t=50+0.4t解此方程得:
0.2t=50.
所以
t=250.
答:如果一个月内通话250分,那么两种计费方式的收费相同.
130元
120元
170元
180元
问题:什么情况下用“全球通”优惠一些?什么情况下用“神州行”优惠一些?
小明想在两种灯中选购一种,其中一种是11瓦(即0.011千瓦)
的节能灯,售价60元;另一种是60瓦(即0.06千瓦)的白炽灯,
售价3元.两种灯的照明效果一样,使用寿命也相同(3
000小
时以上).节能灯售价较高,但是较省电;白炽灯售价低,但是
用电多.如果电费是0.5元/(千瓦时),选哪种灯可以节省费用(灯的售价加电费)?
分析:问题中有以下基本等量关系:
费用=灯的售价+电费;
电费=0.5×灯的功率(千瓦)
×照明时间(时).
【跟踪训练】
(1)设照明时间为t小时,则
总费用
售价
电费
节能灯
60元
白炽灯
3元
(2)用特殊值试探:如果取
t=2
000时,
节能灯的总费用为:60+0.5×0.011t
=60+0.5×0.011×2
000=71;
白炽灯的总费用为:3+0.5×0.06t
=3+0.5×0.06×2
000=63;
60+0.5×0.011t
3+0.5×0.06t
0.5×0.011t
0.5×0.06t
由两组数值可以说明,照明
时间不同,为了省钱而选择
用哪种灯的答案也不同.
如果取t=2
500呢?
请你算一算节能灯与白炽灯哪个费用较低?
解:设照明时间为t小时,
则节能灯的总费用为(60+0.5×0.011t)元;
白炽灯的总费用为(3+0.5×0.06t)元;
如果两个总费用相等,则有
60+0.5×0.011t
=3+0.5×0.06t
解此方程得:t≈2
327(小时)
因此我们可以取t=2
000小时和t=2
500小时,分别计算节能灯和白炽灯的总费用.
当t=2000时,
节能灯的总费用为:
60+0.5×0.011t
=60+0.5×0.011×2
000=71;
白炽灯的总费用为:
3+0.5×0.06t
=3+0.5×0.06×2
000=63;
当t=2500时,
节能灯的总费用为:60+0.5×0.011×2
500=73.75;
白炽灯的总费用为:3+0.5×0.06×2
500=78;
因此由方程的解和试算判断:
在t<2
327小时时,选择白炽灯优惠一些;
在t≈2
327小时时,两种灯的总费用一样;
在t>2
327小时而不超过使用寿命时,选择节能灯优惠一些.
小明想在两种灯中选购一种,其中一种是11瓦(即0.011千
瓦)的节能灯,售价60元;另一种是60瓦(即0.06千瓦)的白
炽灯,售价3元.两种灯的照明效果一样,使用寿命也相同
(3000小时以上).节能灯售价较高,但是较省电;白炽灯售
价低,但是用电多.如果电费是0.5元/(千瓦时),选哪种灯
可以节省费用(灯的售价加电费)?
问题:
如果灯的使用寿命都是3
000小时,而计划照明3
500
小时,则需要购买两个灯,试设计你认为能省钱的选灯方案.
参考方案:买白炽灯和节能灯各一只,用白炽灯照明500小时,
节能灯照明3
000小时.
在这种方案中的总费用为:
60+0.5×0.011×3
000+3+0.5×0.06×500
=60+16.5+3+15
=94.5(元).
你的方案的总费用是多少?
小结:
(1)解决这种问题的关键是什么?
(2)解决这种问题的步骤是什么?
找分界点,确定相等关系
观察,分析,判断,解答,验证
【课后练习】
1.某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电量15万度.如果设上半年每月平均用电x度,则所列方程正确的是(
)
A.6x+6(x-2000)=150000
B.6x+6(x+2000)=150000
C.6x+6(x-2000)=15
D.6x+6(x+2000)=15
2.某班分两组去两处植树,第一组22人,第二组26人.现第一组在植树中遇到困难,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A.22+x=2×26
B.22+x=2(26﹣x)
C.2(22+x)=26﹣x
D.22=2(26﹣x)
3.小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
A.x+5(12﹣x)=48
B.x+5(x﹣12)=48
C.x+12(x﹣5)=48
D.5x+(12﹣x)=48
4.某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地占林地面积的20%,设把x公顷旱地改为林地,则可列方程(
)
A.54?x=20%×108
B.54?x=20%×(108+x
C.54+x=20%×162
D.108?x=20%(54+x)
5.一船在静水中的速度为,水流速度为,从甲码头顺流航行到乙码头,再返回甲码头共用若设甲、乙两码头的距离为xkm,则下列方程正确的是
6.甲、乙两工程队开挖一条水渠各需10天、15天,两队合作2天后,甲有其他任务,剩下的工作由乙队单独做,还需多少天能完成任务?设还需x天,可得方程( )
7.小刚从家跑步到学校,每小时跑12km,会迟到5分钟;若骑自行车,每小时骑15km,则可早到10分钟.设他家到学校的路程是xkm,则根据题意列出方程是( )
8.一项工程,甲独做需10天完成,乙单独做需15天完成,两人合作4天后,剩下的部分由乙独做全部完成,设乙独做x天,由题意得方程( )
9.商店对某种手机的售价作了调整,按原售价的
8
折出售,此时的利润率为
14%,若此种手机的进价为
1200
元,设该手机的原售价为
x
元,则下列方程正确的是(
)
A.0.8x﹣1200=1200×14%
B.0.8x﹣1200=14%x
C.x﹣0.8x=1200×14%
D.0.8x﹣1200=14%×0.8x
10.一游泳池计划注入一定体积的水,按每小时500立方米的速度注水,注水2小时,注水口发生故障,停止注水,经20分钟抢修后,注水速度比原来提高了,结果比预定的时间提前了10分钟完成注水任务,则计划注入水的体积为
11.有一位工人师傅要锻造底面直径为40cm的“矮胖”形圆柱,可他手上只有底面直径是10cm、高为80cm的“瘦长”形圆柱,若不计损耗,则锻造出的“矮胖”形圆柱的高为________.
12.一艘船从甲码头到乙码头顺流行驶,用了2个小时,从乙码头返回甲码头逆流行驶,用了2.5小时,已知水流的速度是3千米/时,则船在静水中的速度是_____千米/时.
13.张老师带学生乘车外出郊游,甲车主说:”不论师生,每人8折,"乙车主说:“学生9折,老师免费,“张老师算了一下,不论坐谁的车,费用一样,则张老师带的学生人数是________.
14.湖园中学学生志愿服务小组在“三月学雷锋”活动中,购买了一批牛奶到敬老院慰问老人,如果送给每位老人2盒牛奶,那么剩下16盒;如果送给每位老人3盒牛奶,则正好送完.设敬老院有x位老人,依题意可列方程为
.
15.一个两位数,个位上的数字是十位上数字的3倍,它们的和是12,那么这个两位数是____.
【课后练习】答案
1.A
2.B
3.A
4.B
5.D
6.A
7.D
8.B
9.A
10.B
11.5cm
12.27
13.8人
14.2x+16=3x.
15.39
