复件 2020上海交通大学自主招生试题(图片版含解析)
文档属性
| 名称 | 复件 2020上海交通大学自主招生试题(图片版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 357.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-01 21:43:39 | ||
图片预览



文档简介
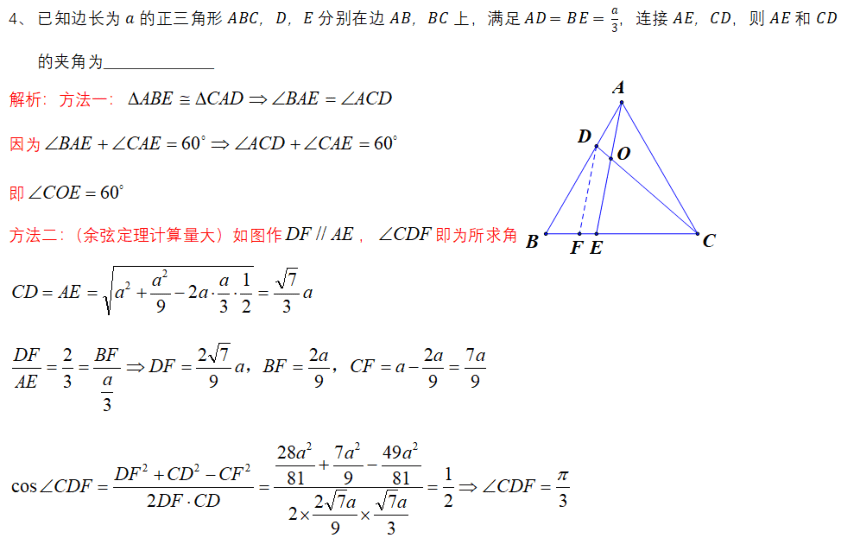
2020上海交通大学自主招生试题
1、函数f(x)的定义域为(0,1),若c∈(0,),则函数g(x)=f(x+c)+f(x-c)的定义域为
0c解析:由题意知
0因为C∈0.,所以c2、已知方程2X-sinx=1,则下列判断:(1)方程没有正数解;(2)方程有无穷多个解;(3)方程有一个正数解;
(4)方程的实根小于1,其中错误的判断有
解析:2=sinx+1转化为函数∫(x)=2与g(x)=sinx+1的交点问题
所以错误的是(1)
y
3、小于1000的正整数中,既不是5的倍数也不是7的倍数的整数有
解析:由题意可知9991000
994980
686
735
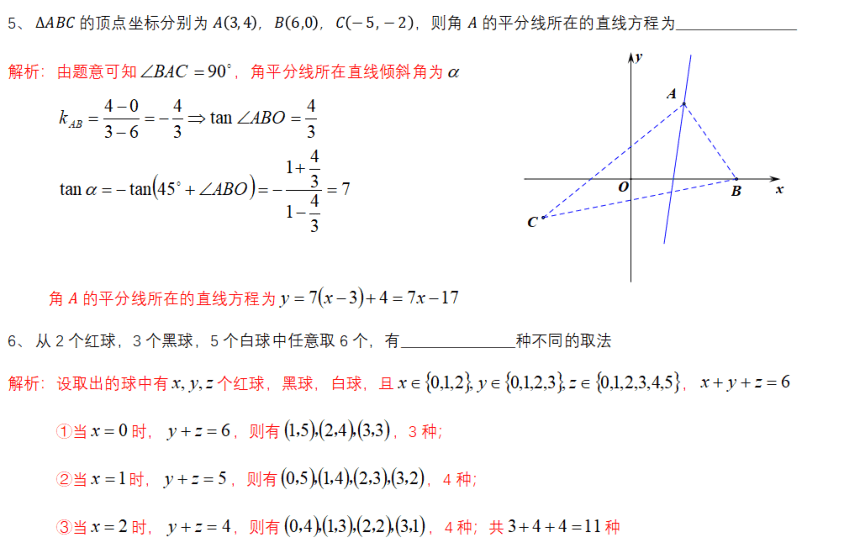
4、已知边长为a的正三角形ABC,D,E分别在边AB,BC上,满足AD=BE=5,连接AE,CD,则AE和CD
的夹角为
解析:方法一:△4BE三△CAD→∠BE=∠ACD
因为∠BEE+∠CAE=60→∠ACD+∠CAE=60
O
即∠COE=60
方法二:(余弦定理计算量大)如图作DF∥AE,∠CDF即为所求角B·FE
C
,d-2a
CD=AE=la+
323
DF2BF→DF2,bF、2a
CF=a
2a
a
ae
3
a
DF+CD'-CF2
28a2
7a
49a
cos∠CDF=
81
8
→∠CDF
2DF.
CD
2√7a√7a2
3
5、△ABC的顶点坐标分别为A(3,4),B(6,0),C(-5,-2),则角A的平分线所在的直线方程为
解析:由题意可知∠BAC=90°,角平分线所在直线倾斜角为a
4-04
→tan∠ABO
434
1+
tanc=-tan(45°+∠ABO
B
角A的平分线所在的直线方程为y=7(x-3)+4=7x-17
6、从2个红球,3个黑球,5个白球中任意取6个,有
种不同的取法
解析:设取出的球中有x,y,二个红球,黑球,白球,且x∈{012y∈{02,3}=∈01,2,345},x+y+:=6
①当x=0时,y+=6,则有(1,5)(24(3,3),3种
2当x=1时,y+=5,则有(05(4)(2,3)(3,2).4种;
3当x=2时,y+二=4,则有0.4(,3)(2,2)3),4种;共3+4+4=11种
7、已知y=ax2+bx+c过A(-3,4),B(54),则2a+b
解析:f(-3)=4,f(5)=4,A、B关于对称轴对称
b-3+5
所以
2a+b=0
2a2
8、过抛物线y2=2px(p>0)的焦点F作直线m交抛物线于A、B两点,若A、B横坐标之和为5,则直线m的条
数为
2
解析:设直线x=+,联立得:
r==1-2n-p2=0
x1+x2=1(y1+y2)+p=5→t
2p
①当P>5时,直线条数为0条
2当p=5时,直线条数为1条
③3当09、用同样大小的正n边形平铺整个平面(没有重叠),若要将平面铺满,则n的值为
解析:设需要个正边形,铺满内角和等于360°
1、函数f(x)的定义域为(0,1),若c∈(0,),则函数g(x)=f(x+c)+f(x-c)的定义域为
0
0
(4)方程的实根小于1,其中错误的判断有
解析:2=sinx+1转化为函数∫(x)=2与g(x)=sinx+1的交点问题
所以错误的是(1)
y
3、小于1000的正整数中,既不是5的倍数也不是7的倍数的整数有
解析:由题意可知9991000
994980
686
735
4、已知边长为a的正三角形ABC,D,E分别在边AB,BC上,满足AD=BE=5,连接AE,CD,则AE和CD
的夹角为
解析:方法一:△4BE三△CAD→∠BE=∠ACD
因为∠BEE+∠CAE=60→∠ACD+∠CAE=60
O
即∠COE=60
方法二:(余弦定理计算量大)如图作DF∥AE,∠CDF即为所求角B·FE
C
,d-2a
CD=AE=la+
323
DF2BF→DF2,bF、2a
CF=a
2a
a
ae
3
a
DF+CD'-CF2
28a2
7a
49a
cos∠CDF=
81
8
→∠CDF
2DF.
CD
2√7a√7a2
3
5、△ABC的顶点坐标分别为A(3,4),B(6,0),C(-5,-2),则角A的平分线所在的直线方程为
解析:由题意可知∠BAC=90°,角平分线所在直线倾斜角为a
4-04
→tan∠ABO
434
1+
tanc=-tan(45°+∠ABO
B
角A的平分线所在的直线方程为y=7(x-3)+4=7x-17
6、从2个红球,3个黑球,5个白球中任意取6个,有
种不同的取法
解析:设取出的球中有x,y,二个红球,黑球,白球,且x∈{012y∈{02,3}=∈01,2,345},x+y+:=6
①当x=0时,y+=6,则有(1,5)(24(3,3),3种
2当x=1时,y+=5,则有(05(4)(2,3)(3,2).4种;
3当x=2时,y+二=4,则有0.4(,3)(2,2)3),4种;共3+4+4=11种
7、已知y=ax2+bx+c过A(-3,4),B(54),则2a+b
解析:f(-3)=4,f(5)=4,A、B关于对称轴对称
b-3+5
所以
2a+b=0
2a2
8、过抛物线y2=2px(p>0)的焦点F作直线m交抛物线于A、B两点,若A、B横坐标之和为5,则直线m的条
数为
2
解析:设直线x=+,联立得:
r==1-2n-p2=0
x1+x2=1(y1+y2)+p=5→t
2p
①当P>5时,直线条数为0条
2当p=5时,直线条数为1条
③3当0
解析:设需要个正边形,铺满内角和等于360°
同课章节目录
