青岛版八年级数学下册7.1 算术平方根课件(共19张PPT)
文档属性
| 名称 | 青岛版八年级数学下册7.1 算术平方根课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-01 21:58:17 | ||
图片预览






文档简介
(共19张PPT)
春天来了,为了使大家的生活环境变得更好,某小区决定在小区的空地建造一个正方形的花坛,如果这个花坛的面积是16平方米,你知道它的边长是多少吗?
教学目标:
1、了解数的算术平方根的概念,会用根号表示一个非负数的算术平方根。
2、了解求一个正数的算术平方根与平方是互逆的运算,会利用这个
互逆运算关系求某些非负数的算术平方根。
3、
理解算术平方根的性质。
7.1
算术平方根
学习目标
1、了解算术平方根的概念,会用根号表示一个非负数的算术平方根。
2、了解求一个非负数的平方运算与求算术平方根互为逆运算的关系,会用平方运算求某些非负数的算术平方根。
重点:算术平方根的概念,会用根号表示一个非负数的算术平方根。
难点:算术平方根概念的理解以及求一个非负数的算术平方根。
请同学们认真研读课本P40,合上课本尝试回答以下问题:
1.
什么是算术平方根?怎样表示?
2.
0的算术平方根是什么?
3.
体会求一个正数的算术平方根与平方的关系
自主学习
5.
下列式子表示什么意思?
4.
负数有算术平方根吗?
(3分钟)
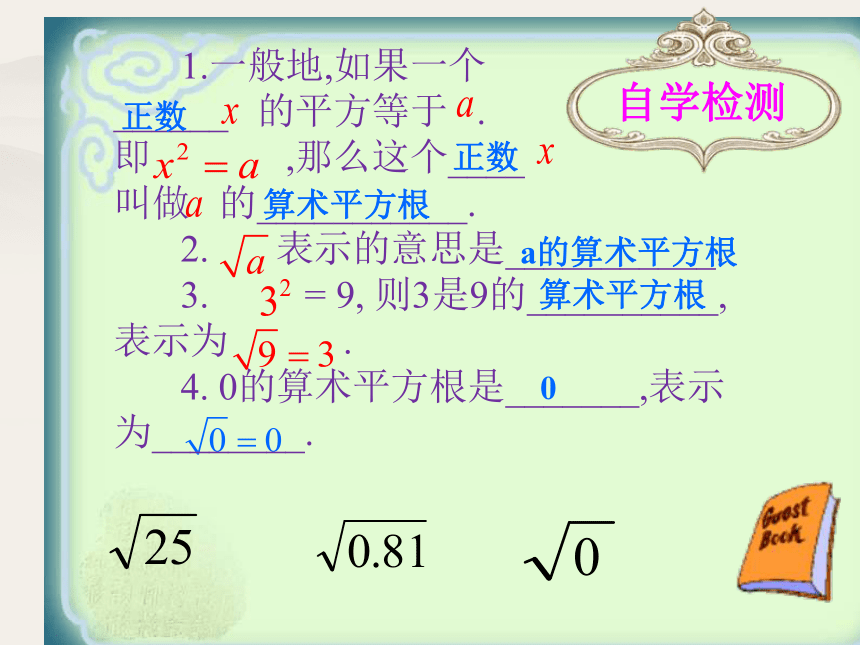
自学检测
1.一般地,如果一个
______
的平方等于
.
即
,那么这个____
叫做
的___________.
2.
表示的意思是___________.
3.
=
9,
则3是9的__________,
表示为
.
4.
0的算术平方根是_______,表示
为________.
正数
正数
算术平方根
a的算术平方根
算术平方根
0
合作探究
(5分钟)
判断题:
①
1/4的算术平方根是±1/2(
)
②
5是(-5)2的算术平方根(
)
③
一个正数的算术平方根总小于它本身(
)
④
-
6是
36
的算术平方根(
)
⑤
0的算术平方根是0(
)
⑥
0.01是0.1的算术平方根(
)
×
√
×
×
√
相信你能行!
×
1.负数有算术平方根吗?
思考:
2.
(
)
=
a
2
如何理解?
1、下列各数没有算术平方根的是(
)
A
0
B
16
C
-4
D
2
2、若实数a的算术平方根等于3,则a的值是(
)
A
3
B
-3
C
-9
D
9
C
D
练习
填空题:
1.
正数的算术平方根是——
2.
0的算术平方根是——
3.
算术平方根是它本身的数是——
4.
(-4)2的算术平方根是——
5.
1/49的算术平方根的相反数的绝对值是——
正数
0或1
0
4
1/7
相信你能行!
例1、下列各式中哪些有意义?哪些无意义?为什么?
答:有意义的是
无意义的是
(
)
2
;
3
;
3
;
3
;
5
-
-
-
例2、铺一间面积为60平方米的教室的地面,需用大小完全相同的240块正方形地板砖,每块地板砖的边长是多少米?
解:设每块地板砖的边长为x米,由题意,得
即
于是
所以,每块地板砖的边长是0.5米
本节课你有什么收获?
1、了解了算术平方根的概念
2、能利用正方形的面积与边长的关系求正数的算术方根并会用符号表示;
注意:
1、根号a(a≥0)表示数a的算术平方根
2、根号a有意义的条件是a≥0,无意义的条件是
a<0
3、0的是算术平方根0,负数没有算术平方根
1、正数的算术平方根是
(
)数
0的算术平方根是
(
)
算术平方根等于它本身的数是
(
)
2、判断题
一个数的算术平方根一定是正数(
)
-64的算术平方根是8
(
)
9是3的算术平方根
(
)
-7是
的算术平方根(
)
2、求下列各数的算术平方根:
①
36
②
达标测试
1、计算
(1)
(2)
2、计算
(1)
(2)
拓展提升
●
算术平方根是非负数.
●
被开方数是非负数.
a≥0
●
0的算术平方根是0
●负数没有算术平方根。
≥0
达标测试
1、正数的算术平方根是(
)数,
0的算术平方根是
(
)算术平方根等于它本身的数是
(
)
2、判断题
一个数的算术平方根一定是正数(
)
-64的算术平方根是8
(
)
9是3的算术平方根
(
)
-7是(-7)2
的算术平方根(
)
2、求下列各数的算术平方根:
①
36
②
作业设置
必做题
课本42页习题7.1复习与巩固
选做题
课本42页习题7.1拓展与延伸
谢谢指导!
春天来了,为了使大家的生活环境变得更好,某小区决定在小区的空地建造一个正方形的花坛,如果这个花坛的面积是16平方米,你知道它的边长是多少吗?
教学目标:
1、了解数的算术平方根的概念,会用根号表示一个非负数的算术平方根。
2、了解求一个正数的算术平方根与平方是互逆的运算,会利用这个
互逆运算关系求某些非负数的算术平方根。
3、
理解算术平方根的性质。
7.1
算术平方根
学习目标
1、了解算术平方根的概念,会用根号表示一个非负数的算术平方根。
2、了解求一个非负数的平方运算与求算术平方根互为逆运算的关系,会用平方运算求某些非负数的算术平方根。
重点:算术平方根的概念,会用根号表示一个非负数的算术平方根。
难点:算术平方根概念的理解以及求一个非负数的算术平方根。
请同学们认真研读课本P40,合上课本尝试回答以下问题:
1.
什么是算术平方根?怎样表示?
2.
0的算术平方根是什么?
3.
体会求一个正数的算术平方根与平方的关系
自主学习
5.
下列式子表示什么意思?
4.
负数有算术平方根吗?
(3分钟)
自学检测
1.一般地,如果一个
______
的平方等于
.
即
,那么这个____
叫做
的___________.
2.
表示的意思是___________.
3.
=
9,
则3是9的__________,
表示为
.
4.
0的算术平方根是_______,表示
为________.
正数
正数
算术平方根
a的算术平方根
算术平方根
0
合作探究
(5分钟)
判断题:
①
1/4的算术平方根是±1/2(
)
②
5是(-5)2的算术平方根(
)
③
一个正数的算术平方根总小于它本身(
)
④
-
6是
36
的算术平方根(
)
⑤
0的算术平方根是0(
)
⑥
0.01是0.1的算术平方根(
)
×
√
×
×
√
相信你能行!
×
1.负数有算术平方根吗?
思考:
2.
(
)
=
a
2
如何理解?
1、下列各数没有算术平方根的是(
)
A
0
B
16
C
-4
D
2
2、若实数a的算术平方根等于3,则a的值是(
)
A
3
B
-3
C
-9
D
9
C
D
练习
填空题:
1.
正数的算术平方根是——
2.
0的算术平方根是——
3.
算术平方根是它本身的数是——
4.
(-4)2的算术平方根是——
5.
1/49的算术平方根的相反数的绝对值是——
正数
0或1
0
4
1/7
相信你能行!
例1、下列各式中哪些有意义?哪些无意义?为什么?
答:有意义的是
无意义的是
(
)
2
;
3
;
3
;
3
;
5
-
-
-
例2、铺一间面积为60平方米的教室的地面,需用大小完全相同的240块正方形地板砖,每块地板砖的边长是多少米?
解:设每块地板砖的边长为x米,由题意,得
即
于是
所以,每块地板砖的边长是0.5米
本节课你有什么收获?
1、了解了算术平方根的概念
2、能利用正方形的面积与边长的关系求正数的算术方根并会用符号表示;
注意:
1、根号a(a≥0)表示数a的算术平方根
2、根号a有意义的条件是a≥0,无意义的条件是
a<0
3、0的是算术平方根0,负数没有算术平方根
1、正数的算术平方根是
(
)数
0的算术平方根是
(
)
算术平方根等于它本身的数是
(
)
2、判断题
一个数的算术平方根一定是正数(
)
-64的算术平方根是8
(
)
9是3的算术平方根
(
)
-7是
的算术平方根(
)
2、求下列各数的算术平方根:
①
36
②
达标测试
1、计算
(1)
(2)
2、计算
(1)
(2)
拓展提升
●
算术平方根是非负数.
●
被开方数是非负数.
a≥0
●
0的算术平方根是0
●负数没有算术平方根。
≥0
达标测试
1、正数的算术平方根是(
)数,
0的算术平方根是
(
)算术平方根等于它本身的数是
(
)
2、判断题
一个数的算术平方根一定是正数(
)
-64的算术平方根是8
(
)
9是3的算术平方根
(
)
-7是(-7)2
的算术平方根(
)
2、求下列各数的算术平方根:
①
36
②
作业设置
必做题
课本42页习题7.1复习与巩固
选做题
课本42页习题7.1拓展与延伸
谢谢指导!
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
