二次函数

(共15张PPT)
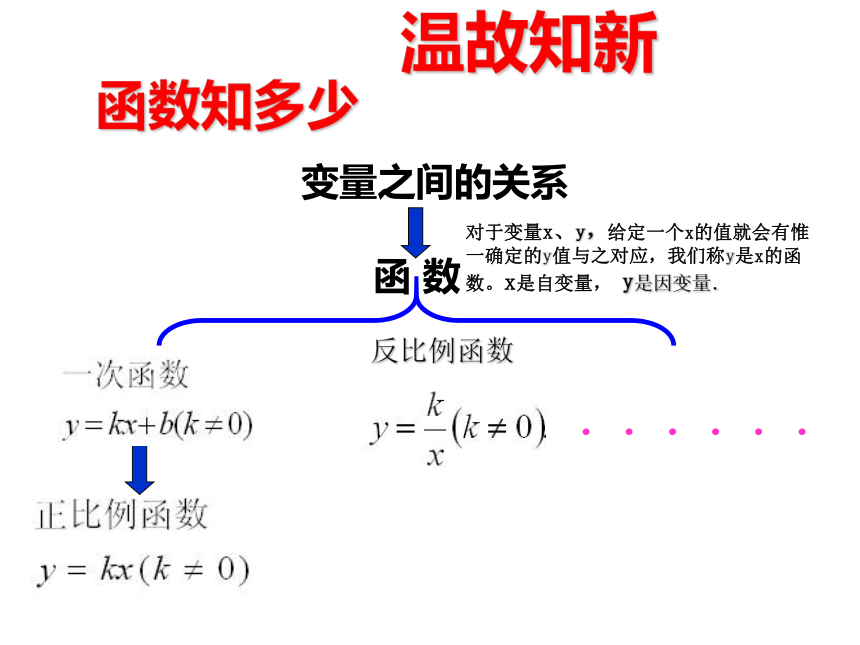
函 数
函数知多少
变量之间的关系
反比例函数
温故知新
．．．．．．
对于变量x、y，给定一个x的值就会有惟一确定的y值与之对应，我们称y是x的函数。x是自变量， y是因变量．
源于生活的数学
我们曾注意过水滴激起的波纹，它不断地向外扩展，所形成的圆周长Ｃ是半径r的一次函数：
容易知道，不断扩大的圆面积Ａ与半径r之间的函数关系是式是：
C=2∏r
A= ∏r2
问题二：
用16m长的篱笆围成长方形的生物园饲养小兔，怎样围可使小兔的活动范围最大？
１．若设：长方形的长是x，宽是y１，则y１与x的函数关系式是：　　　　　　　　　
２．若设长方形的长是x，长方形的面积是
y２，则y２与x的函数关系式是：
　　
y１＝８-x
y２=x(8-x)=-x2+8x
- 1 2 3 3.5 4 4.5 5 6 7 -
y2 - -
7
12
15
15.75
16
15.75
15
12
7
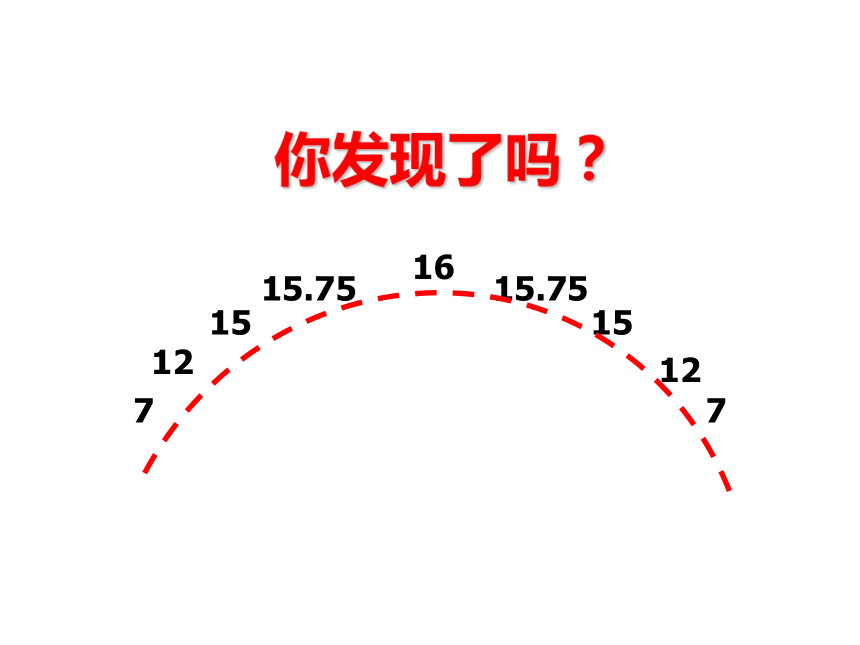
你能根据表格中的数据作出猜想吗
怎样围可使小兔的活动范围最大？
y２=x(8-x)=-x2+8x
12
15
15.75
16
15.75
15
12
7
7
你发现了吗？
亲历知识的发生和发展
要给边长为x米的正方形房间铺设地板，已知某种地板的价格为每平方米240元，踢脚线的价格为每米30元，如果其他费用为1000元，门宽0.8米，那么总费用y为多少元？
y=240x2+120x+976
定义：一般地,形如 ( 是常数, ≠ 0)的函数称为x的二次函数.
其中x是自变量，y是因变量
提示:
(1)右边x的代数式一定是整式, 为常数,
且 ≠0.
(2)等式的右边自变量最高次数为2,可以没有一次项和常数项,但不能没有二次项.
A= ∏r2
y２=x(8-x)=-x2+8x
y=240x2+120x+976
函数的自变量的取值通常有一定的范围，如：上例，
但一般的二次函数的自变量的x可取任意实数．
1.下列函数中,哪些是二次函数？
怎么判断

在实践中感悟
（是）
（是）
（不是）
（是）
（不是）
（不是）
(4)
(2)
2.用总长为60m的篱笆围成矩形场地，场地面积S(m )与矩形一边长a(m)之间的关系是什么？属于哪一种函数？
是二次函数
3．圆的半径是4cm,假设半径增加 cm时,圆的面积增加ycm .
（1）写出y与x之间的函数关系表达式；
（2）当圆的半径分别增加1cm, ,
2cm时,圆的面积各增加多少？
1.定义：一般地,形如 ( 是常数, ≠0)的函数叫做x的二次函数.
小结 拓展
２． ( 是常数, ≠0)
　　的几种不同表示形式:
谢　谢　莅　临　指　导　！
1、物体从某一高度落下,已知下落的高度h(m)与下落的时间t(s)的关系是h=4.9t2,填表表示物体在5s前下落的高度:
t/s 1 2 3 4 5
h/m
练习：
４.９
１９.６
４４.１
７８.４
１２２.５
2.某工厂计划为一批长方体形状的产品涂上油漆,长方体的长和宽相等,高比长多0.5m.
(1).长方体的长和宽用x(m)表示,长方体需要涂漆的表面积S(m2)如何表示
(2).如果涂漆每平米所需要的费用是5元,油漆每个长方体所需要费用用y(元)表示,那么y与x的关系式是什么？
谢　谢　莅　临　指　导　！