二次函数（复习）

(共12张PPT)
(综合提高)
1、已知抛物线
经过点A（x1，0）、B （x2，0）、D（0，y1），其中x1＜x2，△ABD的面积等于12。求这条抛物线的解析式及它的顶点坐标。
2、把抛物线y=-3（x-1）2向上平移k个单位，所得的抛物线与x轴交于点A（x1，
0）和B （x2，0）。如果x12+ x22= ，那么k = 。
3,直线l平行于y=2x,且过点(4,-2)
(1)求l的解析式
(2)求l关于y轴对称的直线l’的解析式
4.以(3,0)为圆心,5为半径画圆 ,与x轴交于
A,B两点,与y轴交于C,D两点
(1),求A,B,C,D四点坐标(C上D下)
(2),求过A,B,C三点的抛物线的解析式
3、（99北京）已知二次函数y=x2+2ax-2b+1和y=-x2+（a-3）x+b2-1的图象都经过x轴上两个不同的点M、N，求a、b的值。
设M （x1，0），N （x2，0），且x1≠ x2，则x1、 x2是方程x2+2ax-2b+1=0的两个根。由根与系数的关系，得x1+ x2=-2a， x1· x2=-2b+1
又∵ x1、 x2是方程-x2+（a-3）x+b2-1 =0的两个根，∴x1+ x2=a-3， x1· x2=1-b2
∴ -2a =a-3且-2b+1 =1-b2，解得a=1，b=0或a=1，b=2。当a=1，b=0，二次函数的图象与x轴只有一个交点，应舍去。∴ a=1，b=2
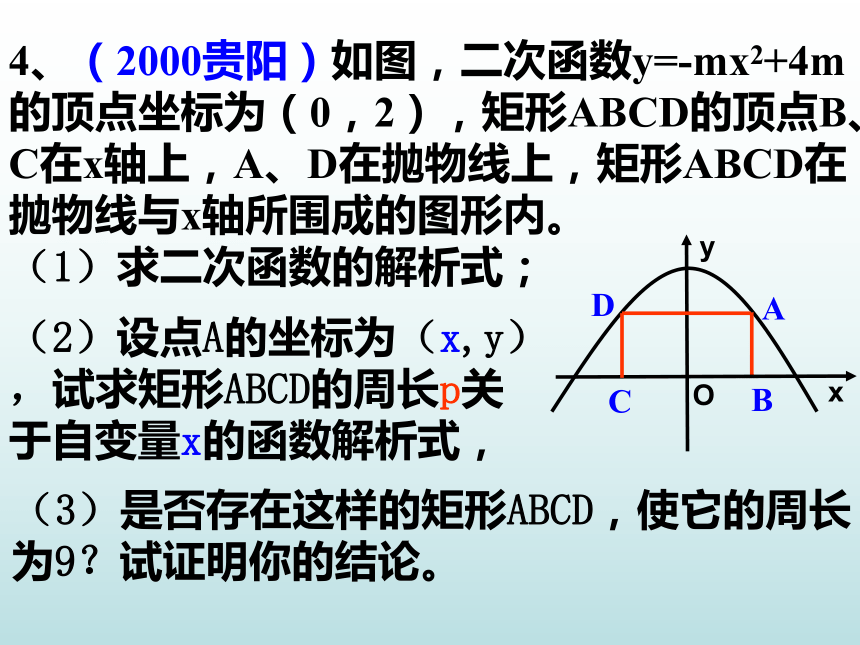
4、（2000贵阳）如图，二次函数y=-mx2+4m的顶点坐标为（0，2），矩形ABCD的顶点B、C在x轴上，A、D在抛物线上，矩形ABCD在抛物线与x轴所围成的图形内。
（1）求二次函数的解析式；
C
A
B
D
x
O
y
（2）设点A的坐标为（x,y）
，试求矩形ABCD的周长p关
于自变量x的函数解析式，
（3）是否存在这样的矩形ABCD，使它的周长
为9？试证明你的结论。
（3）由题意，知：-x2+4|x|+4=9。当x＞0时，
-x2+4x+4=9，方程无实根。当x＜0，-x2-4x+4=9，方程无实根。即矩形ABCD的周长P不可能为9。
5、在体育测试时，初三的一名高个子男生推铅球，已知铅球所经过的路线是某个二次函数的图象的一部分（如图），如果这个男生的出手处A点坐标为（0，2），铅球路线的最高处B的坐标为（6，5）。
（1）求这个二次函数的解析式。
（2）该男生把铅球推出去多远？（精确到0.01米)
实际问题
数学问题
实际问题------求铅球所经过的路线。
求：抛物线的解析式
已知：抛物线的顶点坐标（6，5），并经过A（0，2）
数学问题
解法1：（1）设抛物线的解析式为
y=ax2+bx+c，根据题意可得：
c=2
-b/2a =6
（4ac-b2）/4a =5
∴抛物线的解析式为y=-1/12x2+x+2
（2）当y=0时，-1/12x2+x+2=0
即 x2-12x-24=0。再求出X的值。
a= -1/12
b=1
C=2
解法2：（1）∵抛物线的顶点为（6，5）
∴可设抛物线的解析式为 y=a（x-6）2+5。
∵抛物线经过点A（0，2）
∴2=a（0-6） 2 +5 ∴a=- 1/12
故抛物线的解析式为y=- 1/12（x-6）2+5
即 y=-1/12x2+x+2
（2）当y=0时，
-1/12x2+x+2=0
即 x2-12x-24=0。再求出X的值。