第二章 习题课 匀变速直线运动的推论及初速度为零的比例式的应用—2020-2021【新教材】人教版(2019)高中物理必修第一册课件(共27张PPT)
文档属性
| 名称 | 第二章 习题课 匀变速直线运动的推论及初速度为零的比例式的应用—2020-2021【新教材】人教版(2019)高中物理必修第一册课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-02 00:00:00 | ||
图片预览






文档简介
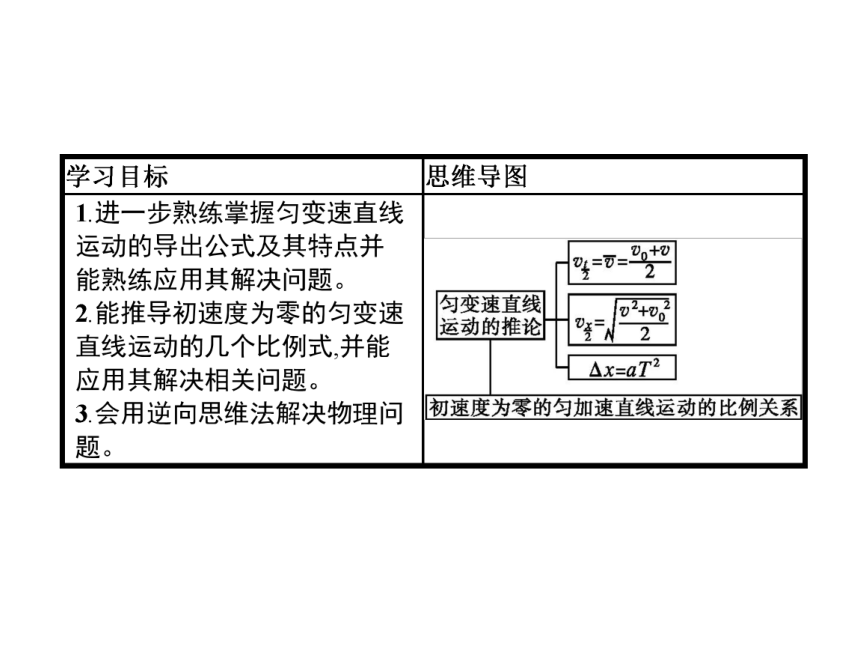
习题课:匀变速直线运动的推论及初速度为零的比例式的应用
问题一
问题二
问题三
随堂检测
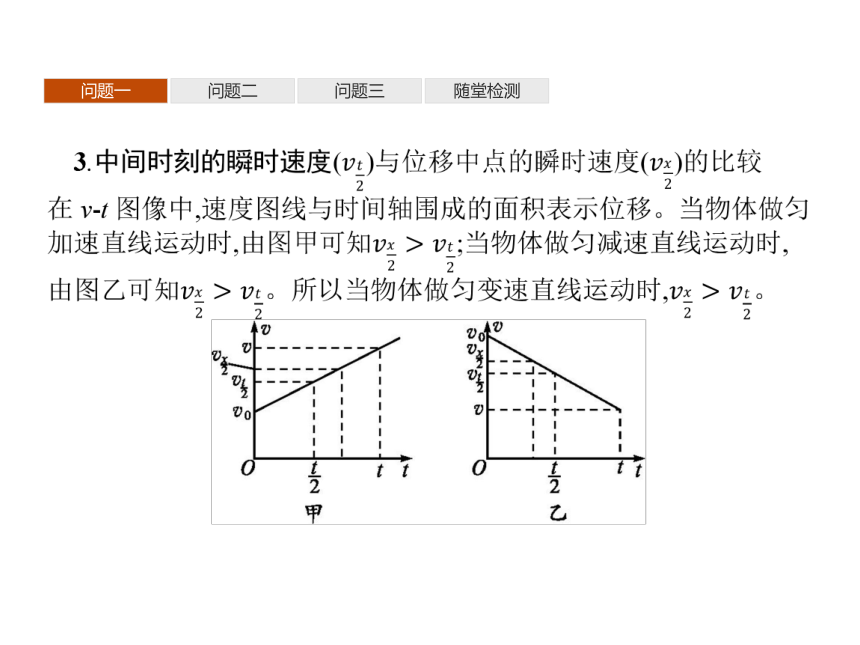
匀变速直线运动的平均速度、中间时刻速度、位移中点速度
情景探究
一辆汽车从A点开始以初速度v0做匀加速直线运动,经过时间t到达B点,再过时间t到达C点时速度为v。利用所学规律能推导出B点的速度吗?B点的速度和AC段的平均速度有什么关系?
问题一
问题二
问题三
随堂检测
知识点拨
1.中间时刻速度与平均速度
(1)内容:做匀变速直线运动的物体,在一段时间t内的平均速度等于这段时间内中间时刻的瞬时速度,还等于这段时间初、末速度矢量和的一半。即:
问题一
问题二
问题三
随堂检测
2.位移中点的速度
(1)内容
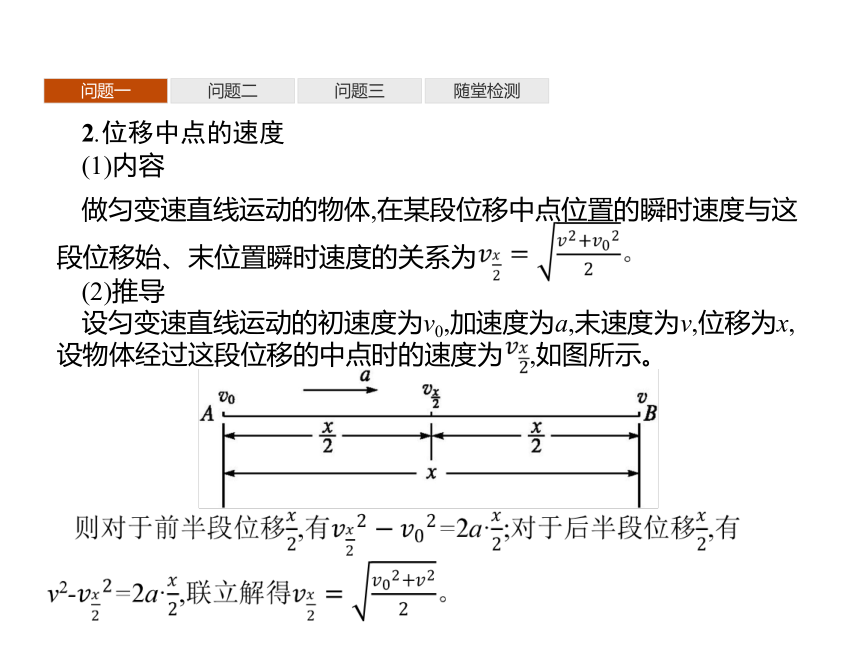
做匀变速直线运动的物体,在某段位移中点位置的瞬时速度与这段位移始、末位置瞬时速度的关系为
(2)推导
设匀变速直线运动的初速度为v0,加速度为a,末速度为v,位移为x,设物体经过这段位移的中点时的速度为 ,如图所示。
问题一
问题二
问题三
随堂检测
问题一
问题二
问题三
随堂检测
实例引导
例1光滑斜面的长度为L,一物体自斜面顶端由静止开始匀加速滑至底端,经历的时间为t,则下列说法不正确的是( )
答案:B
问题一
问题二
问题三
随堂检测
规律方法 是求某时刻瞬时速度的重要方法,要求某时刻的速度,只要求出以该时刻为中间时刻的这段时间的平均速度即可。
问题一
问题二
问题三
随堂检测
变式训练1一个做匀减速直线运动的物体,先后经过a、b两点时的速度大小分别是4v和v,所用时间为t,则下列判断正确的是( )
答案:D
问题一
问题二
问题三
随堂检测
连续相等时间内的位移差公式
情景探究
如图所示为做匀加速直线运动的小车,通过打点计时器打下的纸带,第2个0.02 s小车运动的位移比第1个0.02 s小车运动的位移多多少?第3个0.02 s小车运动的位移比第2个0.02 s小车运动的位移多多少?以此类推,同学们发现有什么规律?
要点提示第2个0.02 s小车运动的位移比第1个0.02 s小车运动的位移多17 mm;第3个0.02 s小车运动的位移比第2个0.02 s小车运动的位移多17 mm;连续相等时间内的位移差相等。
问题一
问题二
问题三
随堂检测
知识点拨
1.内容:做匀变速直线运动的物体,在任意两个连续相等的时间T内的位移差是个常量,即Δx=aT2。
3.拓展:不连续的相等时间内的位移差公式xm-xn=(m-n)aT2,xm为第m段位移,xn为第n段位移。推导过程可用归纳总结的方法得出,如x2-x1=aT2①,x3-x2=aT2②,x4-x3=aT2③,①+②得x3-x1=2aT2,①+②+③得x4-x1=3aT2,②+③得x4-x2=2aT2,最后总结出公式为xm-xn=(m-n)aT2。
问题一
问题二
问题三
随堂检测
例2一小球在桌面上沿直线运动,现用高速摄影机在同一底片上多次曝光,记录下小球每次曝光的位置,并将小球的位置编号。如图所示,1位置恰为小球刚开始运动的瞬间,摄影机连续两次曝光的时间间隔均为1 s,1~6计数点的刻度依次是0、1.5 cm、6.0 cm、13.5 cm、24.0 cm、37.5 cm。则小球的运动性质是 (选填“匀加速直线运动”“变加速直线运动”“匀速直线运动”或“不确定”),小球在该过程中的加速度大小为 m/s2。?
问题一
问题二
问题三
随堂检测
解析:由题图可知,连续相等时间内的位移依次是:x1=1.5 cm,x2=4.5 cm,x3=7.5 cm,x4=10.5 cm,x5=13.5 cm,故其Δx=3.0×10-2 m,小球在连续相等时间内的位移差相等,说明小球做匀加速直线运动;由Δx=x2-x1=aT2得该过程小球的加速度a= m/s2=0.03 m/s2。
答案:匀加速直线运动 0.03
规律方法 利用连续相等时间内的位移差是否相等可以判断物体是否做匀加速直线运动;公式中的T是每一段的时间,不是总时间,公式中的Δx是两段时间位移的差,不是总位移。
问题一
问题二
问题三
随堂检测
变式训练2从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个球后,对在斜面上滚动的小球拍下如图所示的照片,测得xAB=15 cm,xBC=20 cm。试问:
(1)小球的加速度是多少?
(2)拍摄时xCD是多少?
问题一
问题二
问题三
随堂检测
解析:可认为A、B、C、D各点是一个小球在向下运动过程中经过相同时间0.1 s所处的位置。
(2)由于连续相等时间内的位移差恒定,所以xCD-xBC=xBC-xAB
所以xCD=2xBC-xAB=2×20×10-2 m-15×10-2 m=0.25 m。
答案:(1)5 m/s2 (2)0.25 m
问题一
问题二
问题三
随堂检测
初速度为零的匀加速直线运动的比例关系
情景探究
一小车从A点由静止开始做匀加速直线运动(如图所示),若经过时间t到达B点,再经过时间t到达C点,又经过时间t到达D点,那么小车到达B、C、D各点时的速度有什么特点?相邻两点间的距离有什么特点?
要点提示到达B、C、D各点的速度之比是1∶2∶3。AB、BC、CD间的距离比为1∶3∶5。
问题一
问题二
问题三
随堂检测
知识点拨
1.初速度为零的匀加速直线运动,按时间等分(设相等的时间间隔为T)
(1)T末、2T末、3T末、……、nT末瞬时速度之比
v1∶v2∶v3∶……∶vn=1∶2∶3∶……∶n
(2)T内、2T内、3T内、……、nT内的位移之比
x1∶x2∶x3∶……∶xn=12∶22∶32∶……∶n2
(3)第一个T内、第二个T内、第三个T内、……、第n个T内位移之比
xⅠ∶xⅡ∶xⅢ∶……∶xn=1∶3∶5∶……∶(2n-1)
问题一
问题二
问题三
随堂检测
2.初速度为零的匀加速直线运动,按位移等分(设相等的位移为x)
(1)通过前x、前2x、前3x……时的速度之比
(2)通过前x、前2x、前3x……的位移所用时间之比
(3)通过连续相等的位移所用时间之比:
注意①以上比例式成立的条件是物体做初速度为零的匀加速直线运动。②对于末速度为零的匀减速直线运动,可把它看成逆向的初速度为零的匀加速直线运动,应用比例关系,可使问题简化。
问题一
问题二
问题三
随堂检测
实例引导
例3如图所示,一冰壶以速度v垂直边线进入四个矩形区域沿虚线做匀减速直线运动,且刚要离开第四个矩形区域边缘的E点时速度恰好为零,求冰壶依次经过B、C、D时的瞬时速度之比和依次通过后3个矩形区域所用的时间之比。
问题一
问题二
问题三
随堂检测
问题一
问题二
问题三
随堂检测
规律方法 逆向推理法在匀变速直线运动中的应用
(1)末速度为零的匀减速直线运动是初速度为零、加速度大小相等的反向匀加速直线运动的逆向运动。设物体的初速度为v0,加速度大小为a,做匀减速直线运动至速度为零,则可将此运动逆向看成初速度为0、加速度大小为a的匀加速直线运动,末速度为v0。
(2)逆向推理法的优点:逆向推理之后,速度公式v=v0+at变为v=at,位移公式x=v0t+ at2变为x= at2,不仅简化了运算,也使问题变得更加简洁。
(3)处理该类问题时应注意:逆向推理法可简化问题的处理过程,但要注意原过程与逆过程的速度、位移的大小相等,但方向相反。
问题一
问题二
问题三
随堂检测
变式训练3在高11.25 m的屋檐上,每隔一定的时间有一个水滴落下,设水滴的运动是从静止开始的匀加速直线运动。已知第1个水滴落到地面时,第4个水滴刚好离开屋檐。求:第1个水滴落地瞬间空中各相邻两水滴之间的距离。?
问题一
问题二
问题三
随堂检测
解析:设相邻两水滴的时间间隔为T,第1个水滴落到地面时,第4个水滴刚好离开屋檐,中间的时间间隔就是3T。将第4个水滴和第3个水滴之间的距离作为x1,第3个水滴和第2个水滴之间的距离作为x2,第2个水滴和第1个水滴之间的距离作为x3,根据速度从零开始的匀加速直线运动中连续相等时间内的位移之比是x1∶x2∶x3∶……∶xn=1∶3∶5∶……∶(2n-1),整个高度可分为1+3+5=9(份),则x1占1份、x2占3份、x3占5份。
答案:第1、2个水滴之间的距离为6.25 m,第2、3个水滴之间的距离为3.75 m,第3、4个水滴之间的距离为1.25 m。
问题一
问题二
问题三
随堂检测
1.(2019山东滕州高一上期中考试)中国自主研发的“暗剑”无人机,时速可超过2马赫。在某次试飞测试中,起飞前沿地面做匀加速直线运动,加速过程中连续经过两段均为120 m的测试距离,用时分别为2 s和1 s,则无人机的加速度大小是( )
A.20 m/s2 B.40 m/s2 C.60 m/s2 D.80 m/s2
答案:B
问题一
问题二
问题三
随堂检测
2.一物体做匀减速直线运动,初速度为10 m/s,加速度大小为1 m/s2,则物体在停止运动前1 s内的平均速度为( )
A.5.5 m/s B.5 m/s
C.1 m/s D.0.5 m/s
答案:D
解析:物体做匀减速直线运动到静止相当于反向的匀加速直线运动,停止运动前1 s内的平均速度,相当于匀加速运动第1秒内的平均速度,
问题一
问题二
问题三
随堂检测
3.一个物体从静止开始做匀加速直线运动,它在第1 s内与第2 s内位移大小之比为x1∶x2,在走完第1 m时与走完第2 m时的速度大小之比为v1∶v2,则下列说法正确的是( )
A.x1∶x2=1∶3,v1∶v2=1∶2
B.x1∶x2=1∶3,v1∶v2=1∶
C.x1∶x2=1∶4,v1∶v2=1∶2
D.x1∶x2=1∶4,v1∶v2=1∶
答案:B
解析:物体从静止开始做匀加速直线运动,它在连续相等时间内的位移之比x1∶x2∶x3∶……∶xn=1∶3∶5∶……∶(2n-1),所以x1∶x2=1∶3,由v2=2ax得,v1∶v2=1∶ 。
问题一
问题二
问题三
随堂检测
4.有一个做匀变速直线运动的物体,它在两段连续相等的时间内通过的位移分别是24 m和64 m,连续相等的时间为4 s,求物体的初速度和加速度大小。
解析:由x2-x1=aT2,代入数据解得a=2.5 m/s2,再代入x1=vAT+ aT2,可求得vA=1 m/s。
答案:1 m/s 2.5 m/s2
问题一
问题二
问题三
随堂检测
匀变速直线运动的平均速度、中间时刻速度、位移中点速度
情景探究
一辆汽车从A点开始以初速度v0做匀加速直线运动,经过时间t到达B点,再过时间t到达C点时速度为v。利用所学规律能推导出B点的速度吗?B点的速度和AC段的平均速度有什么关系?
问题一
问题二
问题三
随堂检测
知识点拨
1.中间时刻速度与平均速度
(1)内容:做匀变速直线运动的物体,在一段时间t内的平均速度等于这段时间内中间时刻的瞬时速度,还等于这段时间初、末速度矢量和的一半。即:
问题一
问题二
问题三
随堂检测
2.位移中点的速度
(1)内容
做匀变速直线运动的物体,在某段位移中点位置的瞬时速度与这段位移始、末位置瞬时速度的关系为
(2)推导
设匀变速直线运动的初速度为v0,加速度为a,末速度为v,位移为x,设物体经过这段位移的中点时的速度为 ,如图所示。
问题一
问题二
问题三
随堂检测
问题一
问题二
问题三
随堂检测
实例引导
例1光滑斜面的长度为L,一物体自斜面顶端由静止开始匀加速滑至底端,经历的时间为t,则下列说法不正确的是( )
答案:B
问题一
问题二
问题三
随堂检测
规律方法 是求某时刻瞬时速度的重要方法,要求某时刻的速度,只要求出以该时刻为中间时刻的这段时间的平均速度即可。
问题一
问题二
问题三
随堂检测
变式训练1一个做匀减速直线运动的物体,先后经过a、b两点时的速度大小分别是4v和v,所用时间为t,则下列判断正确的是( )
答案:D
问题一
问题二
问题三
随堂检测
连续相等时间内的位移差公式
情景探究
如图所示为做匀加速直线运动的小车,通过打点计时器打下的纸带,第2个0.02 s小车运动的位移比第1个0.02 s小车运动的位移多多少?第3个0.02 s小车运动的位移比第2个0.02 s小车运动的位移多多少?以此类推,同学们发现有什么规律?
要点提示第2个0.02 s小车运动的位移比第1个0.02 s小车运动的位移多17 mm;第3个0.02 s小车运动的位移比第2个0.02 s小车运动的位移多17 mm;连续相等时间内的位移差相等。
问题一
问题二
问题三
随堂检测
知识点拨
1.内容:做匀变速直线运动的物体,在任意两个连续相等的时间T内的位移差是个常量,即Δx=aT2。
3.拓展:不连续的相等时间内的位移差公式xm-xn=(m-n)aT2,xm为第m段位移,xn为第n段位移。推导过程可用归纳总结的方法得出,如x2-x1=aT2①,x3-x2=aT2②,x4-x3=aT2③,①+②得x3-x1=2aT2,①+②+③得x4-x1=3aT2,②+③得x4-x2=2aT2,最后总结出公式为xm-xn=(m-n)aT2。
问题一
问题二
问题三
随堂检测
例2一小球在桌面上沿直线运动,现用高速摄影机在同一底片上多次曝光,记录下小球每次曝光的位置,并将小球的位置编号。如图所示,1位置恰为小球刚开始运动的瞬间,摄影机连续两次曝光的时间间隔均为1 s,1~6计数点的刻度依次是0、1.5 cm、6.0 cm、13.5 cm、24.0 cm、37.5 cm。则小球的运动性质是 (选填“匀加速直线运动”“变加速直线运动”“匀速直线运动”或“不确定”),小球在该过程中的加速度大小为 m/s2。?
问题一
问题二
问题三
随堂检测
解析:由题图可知,连续相等时间内的位移依次是:x1=1.5 cm,x2=4.5 cm,x3=7.5 cm,x4=10.5 cm,x5=13.5 cm,故其Δx=3.0×10-2 m,小球在连续相等时间内的位移差相等,说明小球做匀加速直线运动;由Δx=x2-x1=aT2得该过程小球的加速度a= m/s2=0.03 m/s2。
答案:匀加速直线运动 0.03
规律方法 利用连续相等时间内的位移差是否相等可以判断物体是否做匀加速直线运动;公式中的T是每一段的时间,不是总时间,公式中的Δx是两段时间位移的差,不是总位移。
问题一
问题二
问题三
随堂检测
变式训练2从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个球后,对在斜面上滚动的小球拍下如图所示的照片,测得xAB=15 cm,xBC=20 cm。试问:
(1)小球的加速度是多少?
(2)拍摄时xCD是多少?
问题一
问题二
问题三
随堂检测
解析:可认为A、B、C、D各点是一个小球在向下运动过程中经过相同时间0.1 s所处的位置。
(2)由于连续相等时间内的位移差恒定,所以xCD-xBC=xBC-xAB
所以xCD=2xBC-xAB=2×20×10-2 m-15×10-2 m=0.25 m。
答案:(1)5 m/s2 (2)0.25 m
问题一
问题二
问题三
随堂检测
初速度为零的匀加速直线运动的比例关系
情景探究
一小车从A点由静止开始做匀加速直线运动(如图所示),若经过时间t到达B点,再经过时间t到达C点,又经过时间t到达D点,那么小车到达B、C、D各点时的速度有什么特点?相邻两点间的距离有什么特点?
要点提示到达B、C、D各点的速度之比是1∶2∶3。AB、BC、CD间的距离比为1∶3∶5。
问题一
问题二
问题三
随堂检测
知识点拨
1.初速度为零的匀加速直线运动,按时间等分(设相等的时间间隔为T)
(1)T末、2T末、3T末、……、nT末瞬时速度之比
v1∶v2∶v3∶……∶vn=1∶2∶3∶……∶n
(2)T内、2T内、3T内、……、nT内的位移之比
x1∶x2∶x3∶……∶xn=12∶22∶32∶……∶n2
(3)第一个T内、第二个T内、第三个T内、……、第n个T内位移之比
xⅠ∶xⅡ∶xⅢ∶……∶xn=1∶3∶5∶……∶(2n-1)
问题一
问题二
问题三
随堂检测
2.初速度为零的匀加速直线运动,按位移等分(设相等的位移为x)
(1)通过前x、前2x、前3x……时的速度之比
(2)通过前x、前2x、前3x……的位移所用时间之比
(3)通过连续相等的位移所用时间之比:
注意①以上比例式成立的条件是物体做初速度为零的匀加速直线运动。②对于末速度为零的匀减速直线运动,可把它看成逆向的初速度为零的匀加速直线运动,应用比例关系,可使问题简化。
问题一
问题二
问题三
随堂检测
实例引导
例3如图所示,一冰壶以速度v垂直边线进入四个矩形区域沿虚线做匀减速直线运动,且刚要离开第四个矩形区域边缘的E点时速度恰好为零,求冰壶依次经过B、C、D时的瞬时速度之比和依次通过后3个矩形区域所用的时间之比。
问题一
问题二
问题三
随堂检测
问题一
问题二
问题三
随堂检测
规律方法 逆向推理法在匀变速直线运动中的应用
(1)末速度为零的匀减速直线运动是初速度为零、加速度大小相等的反向匀加速直线运动的逆向运动。设物体的初速度为v0,加速度大小为a,做匀减速直线运动至速度为零,则可将此运动逆向看成初速度为0、加速度大小为a的匀加速直线运动,末速度为v0。
(2)逆向推理法的优点:逆向推理之后,速度公式v=v0+at变为v=at,位移公式x=v0t+ at2变为x= at2,不仅简化了运算,也使问题变得更加简洁。
(3)处理该类问题时应注意:逆向推理法可简化问题的处理过程,但要注意原过程与逆过程的速度、位移的大小相等,但方向相反。
问题一
问题二
问题三
随堂检测
变式训练3在高11.25 m的屋檐上,每隔一定的时间有一个水滴落下,设水滴的运动是从静止开始的匀加速直线运动。已知第1个水滴落到地面时,第4个水滴刚好离开屋檐。求:第1个水滴落地瞬间空中各相邻两水滴之间的距离。?
问题一
问题二
问题三
随堂检测
解析:设相邻两水滴的时间间隔为T,第1个水滴落到地面时,第4个水滴刚好离开屋檐,中间的时间间隔就是3T。将第4个水滴和第3个水滴之间的距离作为x1,第3个水滴和第2个水滴之间的距离作为x2,第2个水滴和第1个水滴之间的距离作为x3,根据速度从零开始的匀加速直线运动中连续相等时间内的位移之比是x1∶x2∶x3∶……∶xn=1∶3∶5∶……∶(2n-1),整个高度可分为1+3+5=9(份),则x1占1份、x2占3份、x3占5份。
答案:第1、2个水滴之间的距离为6.25 m,第2、3个水滴之间的距离为3.75 m,第3、4个水滴之间的距离为1.25 m。
问题一
问题二
问题三
随堂检测
1.(2019山东滕州高一上期中考试)中国自主研发的“暗剑”无人机,时速可超过2马赫。在某次试飞测试中,起飞前沿地面做匀加速直线运动,加速过程中连续经过两段均为120 m的测试距离,用时分别为2 s和1 s,则无人机的加速度大小是( )
A.20 m/s2 B.40 m/s2 C.60 m/s2 D.80 m/s2
答案:B
问题一
问题二
问题三
随堂检测
2.一物体做匀减速直线运动,初速度为10 m/s,加速度大小为1 m/s2,则物体在停止运动前1 s内的平均速度为( )
A.5.5 m/s B.5 m/s
C.1 m/s D.0.5 m/s
答案:D
解析:物体做匀减速直线运动到静止相当于反向的匀加速直线运动,停止运动前1 s内的平均速度,相当于匀加速运动第1秒内的平均速度,
问题一
问题二
问题三
随堂检测
3.一个物体从静止开始做匀加速直线运动,它在第1 s内与第2 s内位移大小之比为x1∶x2,在走完第1 m时与走完第2 m时的速度大小之比为v1∶v2,则下列说法正确的是( )
A.x1∶x2=1∶3,v1∶v2=1∶2
B.x1∶x2=1∶3,v1∶v2=1∶
C.x1∶x2=1∶4,v1∶v2=1∶2
D.x1∶x2=1∶4,v1∶v2=1∶
答案:B
解析:物体从静止开始做匀加速直线运动,它在连续相等时间内的位移之比x1∶x2∶x3∶……∶xn=1∶3∶5∶……∶(2n-1),所以x1∶x2=1∶3,由v2=2ax得,v1∶v2=1∶ 。
问题一
问题二
问题三
随堂检测
4.有一个做匀变速直线运动的物体,它在两段连续相等的时间内通过的位移分别是24 m和64 m,连续相等的时间为4 s,求物体的初速度和加速度大小。
解析:由x2-x1=aT2,代入数据解得a=2.5 m/s2,再代入x1=vAT+ aT2,可求得vA=1 m/s。
答案:1 m/s 2.5 m/s2
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
