1.2.2函数的表示法 同步练习(含解析)
文档属性
| 名称 | 1.2.2函数的表示法 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教新课标A版
必修一
1.2.2函数的表示法
一、单选题
1.下列四个图象中,是函数图象的是(??
)
A.?①????????????????????????????????????B.?①③④????????????????????????????????????C.?①②③????????????????????????????????????D.?③④
2.已知函数
满足
,则
(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
3.已知
是一次函数,且
,则
的解析式为(??
)
A.???????????????????B.???????????????????C.???????????????????D.?
4.已知函数f(x+2)=x2
,
则f(x)等于(???
)
A.?x2+2????????????????????????????????B.?x2-4x+4????????????????????????????????C.?x2-2????????????????????????????????D.?x2+4x+4
5.给出函数f(x),g(x)如表,则
(???
)
x
1
2
3
4
f(x)
4
3
2
1
x
1
2
3
4
g(x)
1
1
3
3
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
6.已知函数
则
(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
7.函数
的图象的大致形状是(???
)
A.????????????B.????????????C.????????????D.?
8.将函数
的图像向右平移1个单位长度,再向上平移3个单位长度,所得的图像所对应的函数解析式为(
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
9.具有性质
的函数,我们称为满足“倒负”变换的函数,给出下列函数:①
;②
;③
其中满足“倒负”变换的函数是(??
)
A.?①③????????????????????????????????????B.?②③????????????????????????????????????C.?①②③????????????????????????????????????D.?①②
10.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.
下列叙述中正确的是(
??)
A.?消耗1升汽油,乙车最多可行驶5千米
B.?以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.?甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.?某城市机动车最高限速80千米/小时.
相同条件下,在该市用丙车比用乙车更省油
二、填空题
11.已知
,则
________.
12.已知
,则
________.
13.已知函数f(x)满足2f(x)+f(-x)=3x
,
则f(x)=________.
14.已知一次函数
满足条件
,则函数
的解析式为
________.
三、解答题
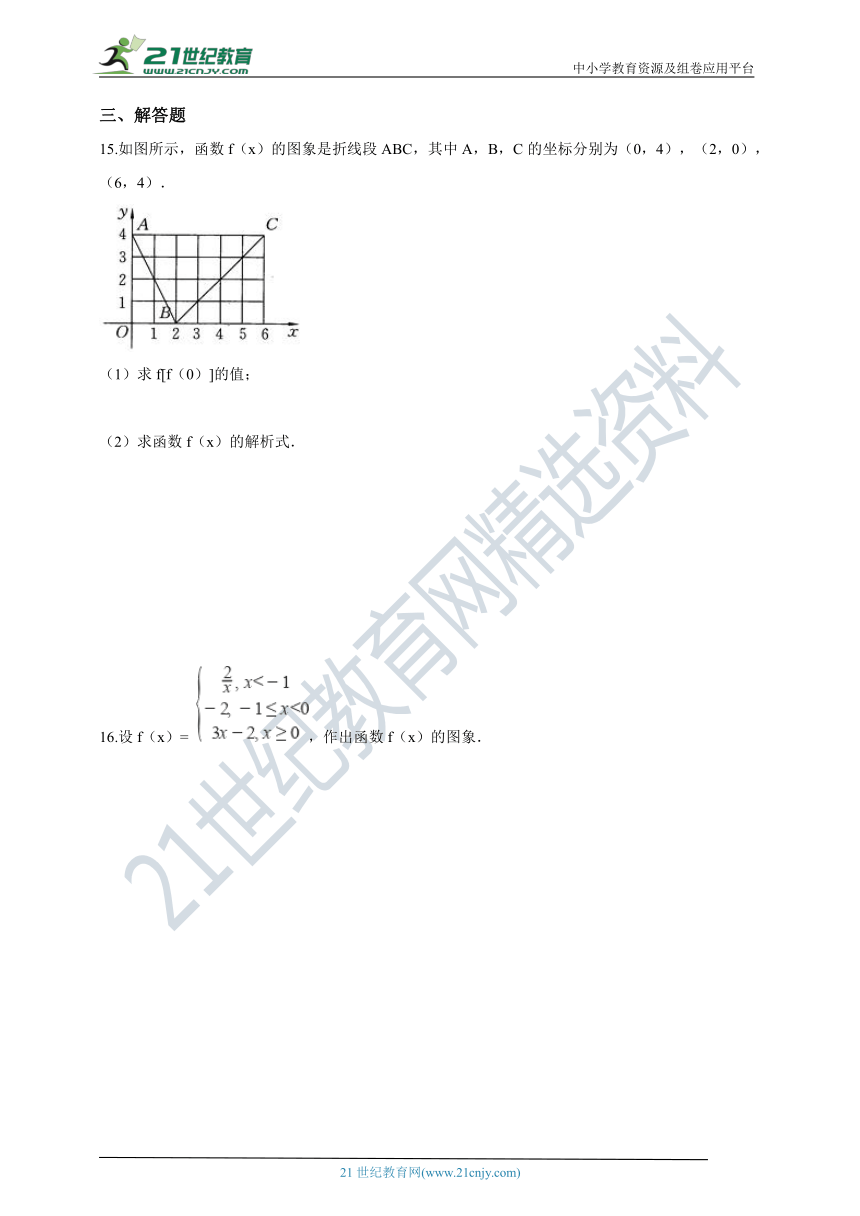
15.如图所示,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4).
(1)求f[f(0)]的值;
(2)求函数f(x)的解析式.
16.设f(x)=
,作出函数f(x)的图象.
17.求下列函数的解析式:
(1)已知f(x)是二次函数,且f(0)=2,f(x+1)-f(x)=x-1,求f(x);
(2)已知3f(x)+2f(-x)=x+3,求f(x).
18.根据条件求下列各函数的解析式:
(1)已知函数f(x+1)=3x+2,则f(x)的解析式;
(2)已知
是一次函数,且满足
,求
的解析式;
(3)已知
满足
,求
的解析式.
答案解析部分
一、单选题
1.答案:
B
解:由函数的定义知,对于定义域中的每一个自变量
,只能有唯一的
与之对应,故②不是函数,①③④是函数.
故答案为:B.
【分析】函数定义中要求:1.两个函数都是非空集合;2.A中的每个元素在B中都有与之对应的元素;3.对应形式为“一对一”或“多对一”,但不能是“一对多”(一个
对应多个
;只有满足了这几个特点的对应关系才是函数关系.本题解题的关键是观察:图象对应的是否是函数;定义域与值域是否正确.
2.答案:
D
解:根据题意得:
①,
令
可得:
②,
联立可得
,
故答案为:D
【分析】由已知利用赋值法,分别令x=2和x=-2列式,联立即可求出的值.
3.答案:
B
解:设
,(
)
∴
,
即
,
所以
,解得
,
,
∴
,
故答案为:B.
【分析】设
,(
),利用
两边恒等求出
即可得结果.
4.答案:
B
解:令
,
故答案为:B.
【分析】利用换元法求函数解析式.
5.答案:
D
解:查表可知,
故答案为:D。
【分析】根据题意,查表格得出
的值,再将结果代入
中,再次查表格即可得出
的值。
6.答案:C
解:由题意得
,
∴
,
∴
.
故答案为:C.
【分析】先用换元法求得f(x)的解析式,在代入求得f(3)的值。
7.答案:
C
解:方法一:
,
观察选项,C符合;
方法二:
,故图像全部在
轴下方,只有C符合,
故答案为:C.
【分析】通过分类讨论去绝对值,得到函数的解析式的分段形式,再观察图像即可得结果.
8.答案:
A
解:设f(x)=2(x+1)2-3,得函数y=2(x+1)2-3的图象向右平移1个单位长度,
得到的图象对应函数解析式为:y=f(x-1)=2[(x+1)-1]2-3=2x2-3,
再将所得图象向上平移3个单位长度,
得到的图象对应函数表达式为:y=f(x-1)+3=2x2-3+3=2x2
,
即最终得到的图象对应函数解析式为:y=2x2
故答案为:A
【分析】函数y=f(x)图象向右平移1个单位长度,得到图象对应的解析式为:y=f(x-1),然后再将所得图象向上平移3个单位长度,得到的图象对应函数表达式为:y=f(x-1)+3.依此规律代入题中函数解析式。
9.答案:
A
解:对于①:
,满足题意;
对于②:
,不满足题意;
对于③,
故
,满足题意.
综上可知,满足“倒负”变换的函数是①③.
故答案为:A.
【分析】对三个函数逐一判断,对于函数①②就是判断
是否成立即可,对于函数③,求出.
的表达式,进行比较即可判断出来.
10.答案:
D
解:对于A,由图象可知当速度大于40km/h时,乙车的燃油效率大于5km/L,
∴当速度大于40km/h时,消耗1升汽油,乙车的行驶距离大于5km,A不符合题意;
对于B,由图象可知当速度相同时,甲车的燃油效率最高,
即当速度相同时,消耗1升汽油,甲车的行驶路程最远,
∴以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,B不符合题意;
对于C,由图象可知当速度为80km/h时,甲车的燃油效率为10km/L,
即甲车行驶10km时,耗油1升,故行驶1小时,路程为80km,燃油为8升,C不符合题意;
对于D,由图象可知当速度小于80km/h时,丙车的燃油效率大于乙车的燃油效率,
∴用丙车比用乙车更省油,D符合题意
故答案为:D.
【分析】根据函数图像的几何意义对每个选项逐一分析即可得出正确答案即可.
二、填空题
11.答案:
解:令
,得
,
,
,因此,
.
故答案为:
.
【分析】先利用换元法求出函数
的解析式,然后可计算出
的值
12.答案:
解:(配凑法)(1)
,
又
∈(-∞,-2]∪[2,+∞),
∴
.
故答案为:
【分析】利用配凑法求出函数的解析式即可.
13.答案:
解:因为2f(x)+f(-x)=3x
,
①
所以将x用-x替换,得2f(-x)+f(x)=-3x
,
②
解由①②组成的方程组得f(x)=3x.
故答案为:3x
【分析】由2f(x)+f(-x)=3x,用-x代入可得2f(-x)+f(x)=-3x,由两式联立解方程组消去f(-x)即可求解出f(x)=3x。
14.答案:
解:设
,
,
,
,
即
,
,
解可得,
,
,
故答案为:
【分析】先设
,
,然后根据
,代入后根据对应系数相等可求
,
,即可求解.
三、解答题
15.答案:
(1)解:f(0)=4,f(4)=2;
(2)解:当0≤x≤2时,设f(x)=kx+b,
代入(0,4)(2,0)
,
∴
,即f(x)=﹣2x+4
当2≤x≤6时,代入(2,0)(6,4),
得
,∴
,
即
f(x)=x﹣2,
综上,
【分析】(1)根据所给的函数图像求得f[f(0)]的值;(2)根据函数图像可知函数是线段AB与线段BC组成的分段函数.
16.答案:解:f(x)=
,
函数的图象为:
【分析】在坐标系中直接画出函数的图象即可.
17.答案:
(1)解:设f(x)=ax2+bx+c(a≠0),
由f(0)=2,得c=2.由f(x+1)-f(x)=x-1,
得恒等式2ax+a+b=x-1,得a=
,b=-
.
故所求函数的解析式为f(x)=
x2-
x+2.
(2)解:由3f(x)+2f(-x)=x+3,①
x用-x代换得3f(-x)+2f(x)=-x+3,②
解①②得f(x)=x+
.
【分析】(1)设二次函数为
,将
与
代入化简,可求得
的值.(2)将
代入原方程得到一个新的方程,和原方程组成方程组,解方程组来求得
的值.
18.答案:
(1)解:设x+1=t,则x=t-1,
∴f(t)=3(t-1)+2=3t-1,
∴f(x)=3x-1.
(2)解:因为
是一次函数,可设
(
),
所以有
,
即
,
因此应有
,解得
.
故
的解析式是
.
(3)解:因为
,①
将
用
替换,得
,②
由①②解得
(
),
即
的解析式是
(
).
【分析】(1)利用换元法即可求出函数f(x)的解析式;(2)设一次函数
(
),代入已知比较系数可得a和b的方程组,解方程组可得结果;(3)将
用
替换,构造方程组即可得到
的解析式.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教新课标A版
必修一
1.2.2函数的表示法
一、单选题
1.下列四个图象中,是函数图象的是(??
)
A.?①????????????????????????????????????B.?①③④????????????????????????????????????C.?①②③????????????????????????????????????D.?③④
2.已知函数
满足
,则
(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
3.已知
是一次函数,且
,则
的解析式为(??
)
A.???????????????????B.???????????????????C.???????????????????D.?
4.已知函数f(x+2)=x2
,
则f(x)等于(???
)
A.?x2+2????????????????????????????????B.?x2-4x+4????????????????????????????????C.?x2-2????????????????????????????????D.?x2+4x+4
5.给出函数f(x),g(x)如表,则
(???
)
x
1
2
3
4
f(x)
4
3
2
1
x
1
2
3
4
g(x)
1
1
3
3
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
6.已知函数
则
(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
7.函数
的图象的大致形状是(???
)
A.????????????B.????????????C.????????????D.?
8.将函数
的图像向右平移1个单位长度,再向上平移3个单位长度,所得的图像所对应的函数解析式为(
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
9.具有性质
的函数,我们称为满足“倒负”变换的函数,给出下列函数:①
;②
;③
其中满足“倒负”变换的函数是(??
)
A.?①③????????????????????????????????????B.?②③????????????????????????????????????C.?①②③????????????????????????????????????D.?①②
10.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.
下列叙述中正确的是(
??)
A.?消耗1升汽油,乙车最多可行驶5千米
B.?以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.?甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.?某城市机动车最高限速80千米/小时.
相同条件下,在该市用丙车比用乙车更省油
二、填空题
11.已知
,则
________.
12.已知
,则
________.
13.已知函数f(x)满足2f(x)+f(-x)=3x
,
则f(x)=________.
14.已知一次函数
满足条件
,则函数
的解析式为
________.
三、解答题
15.如图所示,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4).
(1)求f[f(0)]的值;
(2)求函数f(x)的解析式.
16.设f(x)=
,作出函数f(x)的图象.
17.求下列函数的解析式:
(1)已知f(x)是二次函数,且f(0)=2,f(x+1)-f(x)=x-1,求f(x);
(2)已知3f(x)+2f(-x)=x+3,求f(x).
18.根据条件求下列各函数的解析式:
(1)已知函数f(x+1)=3x+2,则f(x)的解析式;
(2)已知
是一次函数,且满足
,求
的解析式;
(3)已知
满足
,求
的解析式.
答案解析部分
一、单选题
1.答案:
B
解:由函数的定义知,对于定义域中的每一个自变量
,只能有唯一的
与之对应,故②不是函数,①③④是函数.
故答案为:B.
【分析】函数定义中要求:1.两个函数都是非空集合;2.A中的每个元素在B中都有与之对应的元素;3.对应形式为“一对一”或“多对一”,但不能是“一对多”(一个
对应多个
;只有满足了这几个特点的对应关系才是函数关系.本题解题的关键是观察:图象对应的是否是函数;定义域与值域是否正确.
2.答案:
D
解:根据题意得:
①,
令
可得:
②,
联立可得
,
故答案为:D
【分析】由已知利用赋值法,分别令x=2和x=-2列式,联立即可求出的值.
3.答案:
B
解:设
,(
)
∴
,
即
,
所以
,解得
,
,
∴
,
故答案为:B.
【分析】设
,(
),利用
两边恒等求出
即可得结果.
4.答案:
B
解:令
,
故答案为:B.
【分析】利用换元法求函数解析式.
5.答案:
D
解:查表可知,
故答案为:D。
【分析】根据题意,查表格得出
的值,再将结果代入
中,再次查表格即可得出
的值。
6.答案:C
解:由题意得
,
∴
,
∴
.
故答案为:C.
【分析】先用换元法求得f(x)的解析式,在代入求得f(3)的值。
7.答案:
C
解:方法一:
,
观察选项,C符合;
方法二:
,故图像全部在
轴下方,只有C符合,
故答案为:C.
【分析】通过分类讨论去绝对值,得到函数的解析式的分段形式,再观察图像即可得结果.
8.答案:
A
解:设f(x)=2(x+1)2-3,得函数y=2(x+1)2-3的图象向右平移1个单位长度,
得到的图象对应函数解析式为:y=f(x-1)=2[(x+1)-1]2-3=2x2-3,
再将所得图象向上平移3个单位长度,
得到的图象对应函数表达式为:y=f(x-1)+3=2x2-3+3=2x2
,
即最终得到的图象对应函数解析式为:y=2x2
故答案为:A
【分析】函数y=f(x)图象向右平移1个单位长度,得到图象对应的解析式为:y=f(x-1),然后再将所得图象向上平移3个单位长度,得到的图象对应函数表达式为:y=f(x-1)+3.依此规律代入题中函数解析式。
9.答案:
A
解:对于①:
,满足题意;
对于②:
,不满足题意;
对于③,
故
,满足题意.
综上可知,满足“倒负”变换的函数是①③.
故答案为:A.
【分析】对三个函数逐一判断,对于函数①②就是判断
是否成立即可,对于函数③,求出.
的表达式,进行比较即可判断出来.
10.答案:
D
解:对于A,由图象可知当速度大于40km/h时,乙车的燃油效率大于5km/L,
∴当速度大于40km/h时,消耗1升汽油,乙车的行驶距离大于5km,A不符合题意;
对于B,由图象可知当速度相同时,甲车的燃油效率最高,
即当速度相同时,消耗1升汽油,甲车的行驶路程最远,
∴以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,B不符合题意;
对于C,由图象可知当速度为80km/h时,甲车的燃油效率为10km/L,
即甲车行驶10km时,耗油1升,故行驶1小时,路程为80km,燃油为8升,C不符合题意;
对于D,由图象可知当速度小于80km/h时,丙车的燃油效率大于乙车的燃油效率,
∴用丙车比用乙车更省油,D符合题意
故答案为:D.
【分析】根据函数图像的几何意义对每个选项逐一分析即可得出正确答案即可.
二、填空题
11.答案:
解:令
,得
,
,
,因此,
.
故答案为:
.
【分析】先利用换元法求出函数
的解析式,然后可计算出
的值
12.答案:
解:(配凑法)(1)
,
又
∈(-∞,-2]∪[2,+∞),
∴
.
故答案为:
【分析】利用配凑法求出函数的解析式即可.
13.答案:
解:因为2f(x)+f(-x)=3x
,
①
所以将x用-x替换,得2f(-x)+f(x)=-3x
,
②
解由①②组成的方程组得f(x)=3x.
故答案为:3x
【分析】由2f(x)+f(-x)=3x,用-x代入可得2f(-x)+f(x)=-3x,由两式联立解方程组消去f(-x)即可求解出f(x)=3x。
14.答案:
解:设
,
,
,
,
即
,
,
解可得,
,
,
故答案为:
【分析】先设
,
,然后根据
,代入后根据对应系数相等可求
,
,即可求解.
三、解答题
15.答案:
(1)解:f(0)=4,f(4)=2;
(2)解:当0≤x≤2时,设f(x)=kx+b,
代入(0,4)(2,0)
,
∴
,即f(x)=﹣2x+4
当2≤x≤6时,代入(2,0)(6,4),
得
,∴
,
即
f(x)=x﹣2,
综上,
【分析】(1)根据所给的函数图像求得f[f(0)]的值;(2)根据函数图像可知函数是线段AB与线段BC组成的分段函数.
16.答案:解:f(x)=
,
函数的图象为:
【分析】在坐标系中直接画出函数的图象即可.
17.答案:
(1)解:设f(x)=ax2+bx+c(a≠0),
由f(0)=2,得c=2.由f(x+1)-f(x)=x-1,
得恒等式2ax+a+b=x-1,得a=
,b=-
.
故所求函数的解析式为f(x)=
x2-
x+2.
(2)解:由3f(x)+2f(-x)=x+3,①
x用-x代换得3f(-x)+2f(x)=-x+3,②
解①②得f(x)=x+
.
【分析】(1)设二次函数为
,将
与
代入化简,可求得
的值.(2)将
代入原方程得到一个新的方程,和原方程组成方程组,解方程组来求得
的值.
18.答案:
(1)解:设x+1=t,则x=t-1,
∴f(t)=3(t-1)+2=3t-1,
∴f(x)=3x-1.
(2)解:因为
是一次函数,可设
(
),
所以有
,
即
,
因此应有
,解得
.
故
的解析式是
.
(3)解:因为
,①
将
用
替换,得
,②
由①②解得
(
),
即
的解析式是
(
).
【分析】(1)利用换元法即可求出函数f(x)的解析式;(2)设一次函数
(
),代入已知比较系数可得a和b的方程组,解方程组可得结果;(3)将
用
替换,构造方程组即可得到
的解析式.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
