3.2.2函数模型的应用实例 同步练习(含解析)
文档属性
| 名称 | 3.2.2函数模型的应用实例 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-03 11:02:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教新课标A版
必修一
3.2.2函数模型的应用实例
一、单选题
1.函数
,则
(???
)
A.?-1??????????????????????????????????????????B.?1??????????????????????????????????????????C.???????????????????????????????????????????D.?
2.某种产品今年的产量是
,如果保持
的年增长率,那么经过
年
,该产品的产量
满足(???
)
A.??????????
???????B.????????????????
?C.????????????
?????D.?
3.已知函数
若
,则
的取值范围是(
??)
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
4.一个玩具厂一年中12月份的产量是1月份产量的
倍,那么该玩具厂这一年中产量的月平均增长率是(??
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
5.今有一组实验数据如下:
t
1.99
3.0
4.0
5.1
6.12
v
1.5
4.04
7.5
12
18.01
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是(??
)
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
6.《九章算术
衰分》中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱数多少衰出之,问各几何?”翻译为“今有甲持钱
,乙持钱
,丙持钱
,甲、乙、丙三个人一起出关,关税共计
钱,要按个人带钱多少的比例交税,问三人各应付多少税?”则下列说法中错误的是(?
)
A.?甲付的税钱最多??????????????????????????????????????????????????B.?乙、丙两人付的税钱超过甲
C.?乙应出的税钱约为
?????????????????????????????????????????D.?丙付的税钱最少
7.天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(
,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(
)又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
.其中星等为
的星的亮度为
.已知“心宿二”的星等是1.00.“天津四”
的星等是1.25.“心宿二”的亮度是“天津四”的
倍,则与
最接近的是(
)
(当
较小时,
)
A.?1.24?????????????????????????????????????B.?1.25?????????????????????????????????????C.?1.26?????????????????????????????????????D.?1.27
8.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设
,用
表示不超过
的最大整数,则
称为高斯函数,例如:
,
,已知函数
,则函数
的值域是(???
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
9.某建材商场国庆期间搞促销活动,规定:顾客购物总金额不超过800元,不享受任何折扣;如果顾客购物总金额超过800元,则超过800元部分享受一定的折扣优惠,并按下表折扣分别累计计算:
可以享受折扣优惠金额
折扣率
不超过500元的部分
超过500元的部分
若某顾客在此商场获得的折扣金额为50元,则此人购物实际所付金额为
??
A.?1500元???????????????????????????????B.?1550元???????????????????????????????C.?1750元???????????????????????????????D.?1800元
10.函数
=
,则不等式
的解集是(??
)
A.?(
??????????????????????B.?[
??????????????????????C.?(
??????????????????????D.?(
11.设函数
的定义域为R
,
满足
,且当
时,
.若对任意
,都有
,则m的取值范围是(
??)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
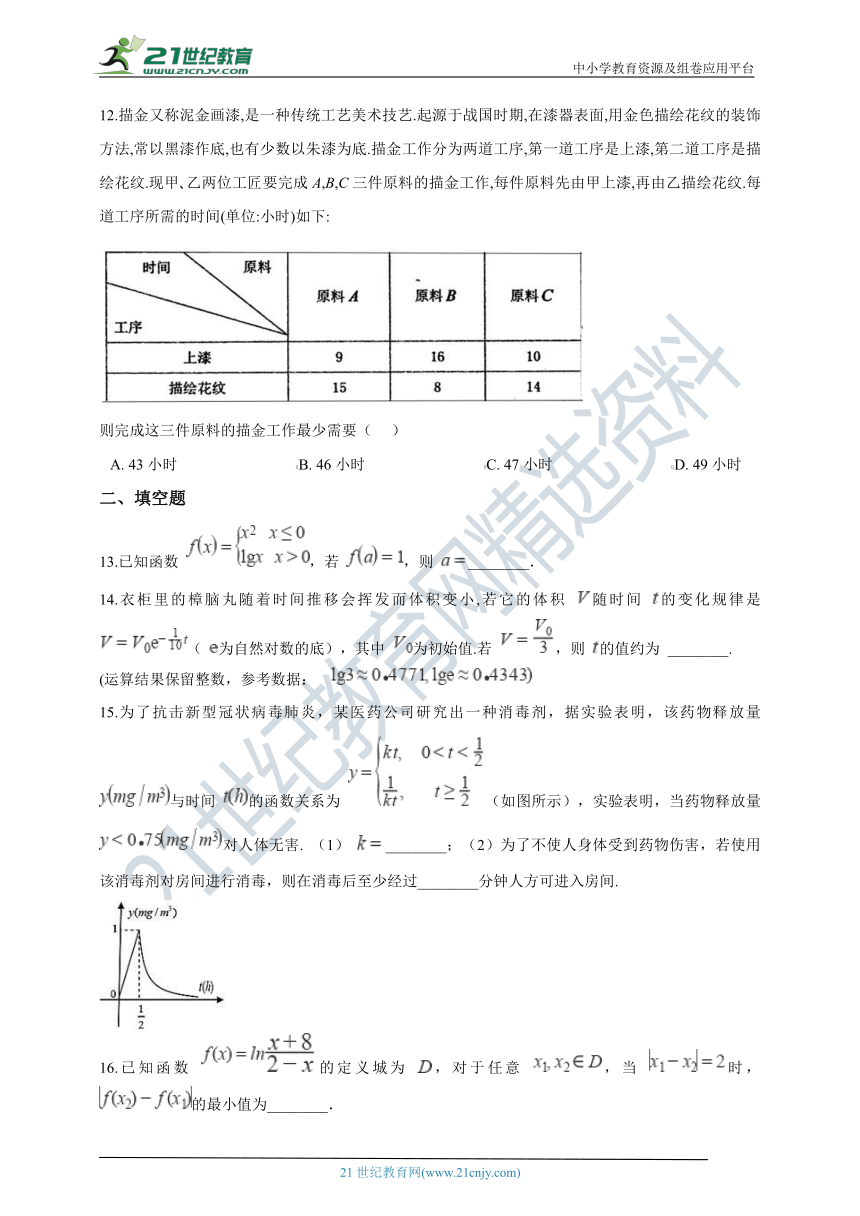
12.描金又称泥金画漆,是一种传统工艺美术技艺.起源于战国时期,在漆器表面,用金色描绘花纹的装饰方法,常以黑漆作底,也有少数以朱漆为底.描金工作分为两道工序,第一道工序是上漆,第二道工序是描绘花纹.现甲?乙两位工匠要完成A,B,C三件原料的描金工作,每件原料先由甲上漆,再由乙描绘花纹.每道工序所需的时间(单位:小时)如下:
则完成这三件原料的描金工作最少需要(???
)
A.?43小时???????????????????????????????B.?46小时???????????????????????????????C.?47小时???????????????????????????????D.?49小时
二、填空题
13.已知函数
,若
,则
________.
14.衣柜里的樟脑丸随着时间推移会挥发而体积变小,若它的体积
随时间
的变化规律是
(
为自然对数的底),其中
为初始值.若
,则
的值约为
________.
(运算结果保留整数,参考数据:
15.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂,据实验表明,该药物释放量
与时间
的函数关系为
(如图所示),实验表明,当药物释放量
对人体无害.
(1)
________;(2)为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,则在消毒后至少经过________分钟人方可进入房间.
16.已知函数
的定义城为
,对于任意
,当
时,
的最小值为________.
三、解答题
17.李庄村某社区电费收取有以下两种方案供农户选择:
方案一:每户每月收管理费2元,月用电不超过30度,每度0.4元,超过30度时,超过部分按每度0.5元.
方案二:不收管理费,每度0.48元.
(1)求方案一收费
元与用电量
(度)间的函数关系;
(2)小李家九月份按方案一交费34元,问小李家该月用电多少度?
(3)小李家月用电量在什么范围时,选择方案一比选择方案二更好?
18.中国第一高摩天轮“南昌之星摩天轮”高度为
,其中心
距地面
,半径为
,若某人从最低点
处登上摩天轮,摩天轮匀速旋转,那么此人与地面的距离将随时间
变化,
后达到最高点,从登上摩天轮时开始计时.
(1)求出人与地面距离y与时间t的函数解析式;
(2)从登上摩天轮到旋转一周过程中,有多长时间人与地面距离大于
.
19.某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量
(单位:微克)与时间
(单位:小时)之间近似满足如图所示的曲线.
(1)写出第一次服药后
与
之间的函数关系式;
(2)据进一步测定:每毫升血液中含药量不少于
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到
,参考数据:
)
答案解析部分
一、单选题
1.答案:
A
解:依题意得
,
故答案为:A
【分析】由已知分段函数的解析式,分两种情况代入即可求值.
2.答案:
D
解:今年产量为
,经过
年后产量为
,
经过
年后产量为
,
以此类推,经过
年后产量为
.
故答案为:D.
【分析】根据增长率,求得经过
年后的产量.
3.答案:
B
解:∵
,
∴
或
即
或
即
∴
的取值范围是
故答案为:B
【分析】依题意,对a分a
与a
讨论,再解相应的不等式即可.
4.答案:
A
解:设月平均增长率为
,一月份的产量为
一年中
月份的产量是
月份产量的
倍,
即
故答案为:
【分析】设月平均增长率为
,建立方程关系,进行求解即可.
5.答案:
C
解:由表可知:
随着
的增大而增大;所以B不适合;
A:
所以A不接近;
C
,
C接近;
D:
D不接近;
故答案为:C
【分析】由表可知
随着
的增大而增大,分别判断各选项中的函数,即可得结果.
6.答案:
B
解:甲付的税钱最多、丙付的税钱最少,可知
正确;
乙、丙两人付的税钱占总税钱的
不超过甲,可知
错误;
乙应出的税钱为
,可知
正确.
故答案为:B
【分析】通过阅读可以知道
说法的正确性,通过计算可以知道
说法的正确性.
7.答案:
C
解:根据题意可得:
可得
,解得
,
根据参考公式可得
,
故与
最接近的是
.
故选:C.
【分析】根据题意,代值计算,即可得
,再结合参考公式,即可估算出结果.
8.答案:
D
解:函数
,
当
时,
;
当
时,
;
当
时,
,
函数
的值域是
,
故答案为:D.
【分析】化简函数
,根据
表示不超过
的最大整数,可得结果.
9.答案:
A
解:设此商场购物总金额为
元,可以获得的折扣金额为
元,
由题设可知:
,
因为
,所以
,
所以
,解得
,
故此人购物实际所付金额为
(元),
故答案为:A.
【分析】设此商场购物总金额为
元,可以获得的折扣金额为
元,可得到获得的折扣金额
元与购物总金额
元之间的解析式,结合
,代入可得某人在此商场购物总金额,减去折扣可得答案.
10.答案:
A
解:∵不等式x+(x+2)f(x+2)≤5,∴x+2+(x+2)f(x+2)≤7,
当x+2≥0时,f(x+2)=1,代入原不等式得:x+2+x+2≤7?-2≤x≤
;
当x+2<0时,f(x+2)=-1,代入原不等式得:x+2-x-2≤7?0≤7,即x<-2;
综上,原不等式的解集为(-∞,
].
故答案为:A
.
【分析】利用分段函数的解析式结合分类讨论的方法求出不等式的解集。
11.答案:
B
解:由f(x+1)=2f(x)知,f(x+t)=
,
,即f(x)=
,
,
当
时,
,此时
,
当-1,,即
,
则
时,
,时,
,
若
,
,则
,
当
时,
,
令
,解得
或
,
由于
时,
,则
。
故答案为:B
【分析】首先根据已知条件求出函数f(x)的解析式,对x分情况讨论得出每个范围内的f(x)的取值范围,并把几种情况并起来即可得出m的取值范围即可。
12.答案:
B
解:由题意,甲按A,C,B的顺序工作,所需时间最短,
最短时间为:
小时,
故选:B
【分析】甲按A,C,B的顺序工作,乙就不会中途没事情做,所需时间最短.
二、填空题
13.答案:
-1或10
解:当
时,
,,
当
时,
,,
综上:
或
.
故答案为:-1或10
【分析】首先根据分段函数的定义域,设
和
,分别代入函数解方程.
14.答案:
11
解:由题意,设一个现樟脑变为
时,需要经过的时间为
,
则
,即
,
所以
,
所以
.
【分析】由已知樟脑丸的体积
随时间
的变化规律是
,
把
代入,利用指数与对数的运算性质,即可求出
的值.
15.答案:
2;40
解:⑴由图可知,当
时,
,即
⑵由题意可得
,解得
则为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,
则在消毒后至少经过
分钟人方可进入房间.
故答案为:(1)2;(2)40
【分析】(1)由
时,
,即可得出
的值;(2)解不等式组
,即可得答案.
16.答案:
解:因为
,所以
的定义域为
,
不妨设
,因为
,所以
,
,
故当取得最小值时,即
时,此时
取得最小值,
即.
故答案为:
【分析】不妨设
,得
,化简
,根据对数函数单调性即可求解.
三、解答题
17.答案:
(1)解:当
时,
;
当
时,
,
∴
(2)解:当
时,由
,解得
,舍去;
当
时,由
,解得
,
∴李刚家该月用电70度;
(3)解:设按第二方案收费为
元,则
,
当
时,由
,
解得:
,解得:
,
∴
;
当
时,由
,
得:
,解得:
,
∴
;
综上,
.
故李刚家月用电量在25度到50度范围内(不含25度、50度)时,
选择方案一比方案二更好.
【分析】⑴分
,
两种情况讨论即可;⑵通过分别令当
时,
时,计算
即可得到答案;⑶通过分别令当
时,
时,由
,计算即可得到结论
18.答案:
(1)解:根据题意摩天轮从最低点开始,
后达到最高点,
则
转一圈,所以摩天轮的角速度为
.
则
时,人在点
处,则此时转过的角度为
.
所以
.
(2)解:登上摩天轮到旋转一周,
则
,
人与地面距离大于
,
即
,
所以
,
由
,解得
,
所以人与地面距离大于
的时间为
分钟,
故有20分钟人与地面距离大于
.
【分析】(1)计算
,得到
时,转过的角度为
,得到解析式.(2)解不等式
得到答案.
19.答案:
(1)解:根据图象知:当
时,
;
当
时,
,由
时,
得
所以
,即
因此
(2)解:根据题意知:
当
时,
;
当
时,
所以
所以
,
因此服药
小时(即
分钟)开始有治疗效果,治疗效果能持续
小时.
【分析】(1)
根据图象得到当
时,
,当
时,
,把
时,
代入求出,即可写出第一次服药后
与
之间的函数关系式;
(2)由(1)
与
之间的函数关系式,当
时,
,当
时,
,
计算得到
,即可判断服药
小时(即
分钟)开始有治疗效果,治疗效果能持续
小时.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教新课标A版
必修一
3.2.2函数模型的应用实例
一、单选题
1.函数
,则
(???
)
A.?-1??????????????????????????????????????????B.?1??????????????????????????????????????????C.???????????????????????????????????????????D.?
2.某种产品今年的产量是
,如果保持
的年增长率,那么经过
年
,该产品的产量
满足(???
)
A.??????????
???????B.????????????????
?C.????????????
?????D.?
3.已知函数
若
,则
的取值范围是(
??)
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
4.一个玩具厂一年中12月份的产量是1月份产量的
倍,那么该玩具厂这一年中产量的月平均增长率是(??
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
5.今有一组实验数据如下:
t
1.99
3.0
4.0
5.1
6.12
v
1.5
4.04
7.5
12
18.01
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是(??
)
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
6.《九章算术
衰分》中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱数多少衰出之,问各几何?”翻译为“今有甲持钱
,乙持钱
,丙持钱
,甲、乙、丙三个人一起出关,关税共计
钱,要按个人带钱多少的比例交税,问三人各应付多少税?”则下列说法中错误的是(?
)
A.?甲付的税钱最多??????????????????????????????????????????????????B.?乙、丙两人付的税钱超过甲
C.?乙应出的税钱约为
?????????????????????????????????????????D.?丙付的税钱最少
7.天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(
,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(
)又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
.其中星等为
的星的亮度为
.已知“心宿二”的星等是1.00.“天津四”
的星等是1.25.“心宿二”的亮度是“天津四”的
倍,则与
最接近的是(
)
(当
较小时,
)
A.?1.24?????????????????????????????????????B.?1.25?????????????????????????????????????C.?1.26?????????????????????????????????????D.?1.27
8.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设
,用
表示不超过
的最大整数,则
称为高斯函数,例如:
,
,已知函数
,则函数
的值域是(???
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
9.某建材商场国庆期间搞促销活动,规定:顾客购物总金额不超过800元,不享受任何折扣;如果顾客购物总金额超过800元,则超过800元部分享受一定的折扣优惠,并按下表折扣分别累计计算:
可以享受折扣优惠金额
折扣率
不超过500元的部分
超过500元的部分
若某顾客在此商场获得的折扣金额为50元,则此人购物实际所付金额为
??
A.?1500元???????????????????????????????B.?1550元???????????????????????????????C.?1750元???????????????????????????????D.?1800元
10.函数
=
,则不等式
的解集是(??
)
A.?(
??????????????????????B.?[
??????????????????????C.?(
??????????????????????D.?(
11.设函数
的定义域为R
,
满足
,且当
时,
.若对任意
,都有
,则m的取值范围是(
??)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
12.描金又称泥金画漆,是一种传统工艺美术技艺.起源于战国时期,在漆器表面,用金色描绘花纹的装饰方法,常以黑漆作底,也有少数以朱漆为底.描金工作分为两道工序,第一道工序是上漆,第二道工序是描绘花纹.现甲?乙两位工匠要完成A,B,C三件原料的描金工作,每件原料先由甲上漆,再由乙描绘花纹.每道工序所需的时间(单位:小时)如下:
则完成这三件原料的描金工作最少需要(???
)
A.?43小时???????????????????????????????B.?46小时???????????????????????????????C.?47小时???????????????????????????????D.?49小时
二、填空题
13.已知函数
,若
,则
________.
14.衣柜里的樟脑丸随着时间推移会挥发而体积变小,若它的体积
随时间
的变化规律是
(
为自然对数的底),其中
为初始值.若
,则
的值约为
________.
(运算结果保留整数,参考数据:
15.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂,据实验表明,该药物释放量
与时间
的函数关系为
(如图所示),实验表明,当药物释放量
对人体无害.
(1)
________;(2)为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,则在消毒后至少经过________分钟人方可进入房间.
16.已知函数
的定义城为
,对于任意
,当
时,
的最小值为________.
三、解答题
17.李庄村某社区电费收取有以下两种方案供农户选择:
方案一:每户每月收管理费2元,月用电不超过30度,每度0.4元,超过30度时,超过部分按每度0.5元.
方案二:不收管理费,每度0.48元.
(1)求方案一收费
元与用电量
(度)间的函数关系;
(2)小李家九月份按方案一交费34元,问小李家该月用电多少度?
(3)小李家月用电量在什么范围时,选择方案一比选择方案二更好?
18.中国第一高摩天轮“南昌之星摩天轮”高度为
,其中心
距地面
,半径为
,若某人从最低点
处登上摩天轮,摩天轮匀速旋转,那么此人与地面的距离将随时间
变化,
后达到最高点,从登上摩天轮时开始计时.
(1)求出人与地面距离y与时间t的函数解析式;
(2)从登上摩天轮到旋转一周过程中,有多长时间人与地面距离大于
.
19.某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量
(单位:微克)与时间
(单位:小时)之间近似满足如图所示的曲线.
(1)写出第一次服药后
与
之间的函数关系式;
(2)据进一步测定:每毫升血液中含药量不少于
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到
,参考数据:
)
答案解析部分
一、单选题
1.答案:
A
解:依题意得
,
故答案为:A
【分析】由已知分段函数的解析式,分两种情况代入即可求值.
2.答案:
D
解:今年产量为
,经过
年后产量为
,
经过
年后产量为
,
以此类推,经过
年后产量为
.
故答案为:D.
【分析】根据增长率,求得经过
年后的产量.
3.答案:
B
解:∵
,
∴
或
即
或
即
∴
的取值范围是
故答案为:B
【分析】依题意,对a分a
与a
讨论,再解相应的不等式即可.
4.答案:
A
解:设月平均增长率为
,一月份的产量为
一年中
月份的产量是
月份产量的
倍,
即
故答案为:
【分析】设月平均增长率为
,建立方程关系,进行求解即可.
5.答案:
C
解:由表可知:
随着
的增大而增大;所以B不适合;
A:
所以A不接近;
C
,
C接近;
D:
D不接近;
故答案为:C
【分析】由表可知
随着
的增大而增大,分别判断各选项中的函数,即可得结果.
6.答案:
B
解:甲付的税钱最多、丙付的税钱最少,可知
正确;
乙、丙两人付的税钱占总税钱的
不超过甲,可知
错误;
乙应出的税钱为
,可知
正确.
故答案为:B
【分析】通过阅读可以知道
说法的正确性,通过计算可以知道
说法的正确性.
7.答案:
C
解:根据题意可得:
可得
,解得
,
根据参考公式可得
,
故与
最接近的是
.
故选:C.
【分析】根据题意,代值计算,即可得
,再结合参考公式,即可估算出结果.
8.答案:
D
解:函数
,
当
时,
;
当
时,
;
当
时,
,
函数
的值域是
,
故答案为:D.
【分析】化简函数
,根据
表示不超过
的最大整数,可得结果.
9.答案:
A
解:设此商场购物总金额为
元,可以获得的折扣金额为
元,
由题设可知:
,
因为
,所以
,
所以
,解得
,
故此人购物实际所付金额为
(元),
故答案为:A.
【分析】设此商场购物总金额为
元,可以获得的折扣金额为
元,可得到获得的折扣金额
元与购物总金额
元之间的解析式,结合
,代入可得某人在此商场购物总金额,减去折扣可得答案.
10.答案:
A
解:∵不等式x+(x+2)f(x+2)≤5,∴x+2+(x+2)f(x+2)≤7,
当x+2≥0时,f(x+2)=1,代入原不等式得:x+2+x+2≤7?-2≤x≤
;
当x+2<0时,f(x+2)=-1,代入原不等式得:x+2-x-2≤7?0≤7,即x<-2;
综上,原不等式的解集为(-∞,
].
故答案为:A
.
【分析】利用分段函数的解析式结合分类讨论的方法求出不等式的解集。
11.答案:
B
解:由f(x+1)=2f(x)知,f(x+t)=
,
,即f(x)=
,
,
当
时,
,此时
,
当-1
,
则
时,
,时,
,
若
,
,则
,
当
时,
,
令
,解得
或
,
由于
时,
,则
。
故答案为:B
【分析】首先根据已知条件求出函数f(x)的解析式,对x分情况讨论得出每个范围内的f(x)的取值范围,并把几种情况并起来即可得出m的取值范围即可。
12.答案:
B
解:由题意,甲按A,C,B的顺序工作,所需时间最短,
最短时间为:
小时,
故选:B
【分析】甲按A,C,B的顺序工作,乙就不会中途没事情做,所需时间最短.
二、填空题
13.答案:
-1或10
解:当
时,
,,
当
时,
,,
综上:
或
.
故答案为:-1或10
【分析】首先根据分段函数的定义域,设
和
,分别代入函数解方程.
14.答案:
11
解:由题意,设一个现樟脑变为
时,需要经过的时间为
,
则
,即
,
所以
,
所以
.
【分析】由已知樟脑丸的体积
随时间
的变化规律是
,
把
代入,利用指数与对数的运算性质,即可求出
的值.
15.答案:
2;40
解:⑴由图可知,当
时,
,即
⑵由题意可得
,解得
则为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,
则在消毒后至少经过
分钟人方可进入房间.
故答案为:(1)2;(2)40
【分析】(1)由
时,
,即可得出
的值;(2)解不等式组
,即可得答案.
16.答案:
解:因为
,所以
的定义域为
,
不妨设
,因为
,所以
,
,
故当取得最小值时,即
时,此时
取得最小值,
即.
故答案为:
【分析】不妨设
,得
,化简
,根据对数函数单调性即可求解.
三、解答题
17.答案:
(1)解:当
时,
;
当
时,
,
∴
(2)解:当
时,由
,解得
,舍去;
当
时,由
,解得
,
∴李刚家该月用电70度;
(3)解:设按第二方案收费为
元,则
,
当
时,由
,
解得:
,解得:
,
∴
;
当
时,由
,
得:
,解得:
,
∴
;
综上,
.
故李刚家月用电量在25度到50度范围内(不含25度、50度)时,
选择方案一比方案二更好.
【分析】⑴分
,
两种情况讨论即可;⑵通过分别令当
时,
时,计算
即可得到答案;⑶通过分别令当
时,
时,由
,计算即可得到结论
18.答案:
(1)解:根据题意摩天轮从最低点开始,
后达到最高点,
则
转一圈,所以摩天轮的角速度为
.
则
时,人在点
处,则此时转过的角度为
.
所以
.
(2)解:登上摩天轮到旋转一周,
则
,
人与地面距离大于
,
即
,
所以
,
由
,解得
,
所以人与地面距离大于
的时间为
分钟,
故有20分钟人与地面距离大于
.
【分析】(1)计算
,得到
时,转过的角度为
,得到解析式.(2)解不等式
得到答案.
19.答案:
(1)解:根据图象知:当
时,
;
当
时,
,由
时,
得
所以
,即
因此
(2)解:根据题意知:
当
时,
;
当
时,
所以
所以
,
因此服药
小时(即
分钟)开始有治疗效果,治疗效果能持续
小时.
【分析】(1)
根据图象得到当
时,
,当
时,
,把
时,
代入求出,即可写出第一次服药后
与
之间的函数关系式;
(2)由(1)
与
之间的函数关系式,当
时,
,当
时,
,
计算得到
,即可判断服药
小时(即
分钟)开始有治疗效果,治疗效果能持续
小时.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
