《余角和补角》教学课件
图片预览



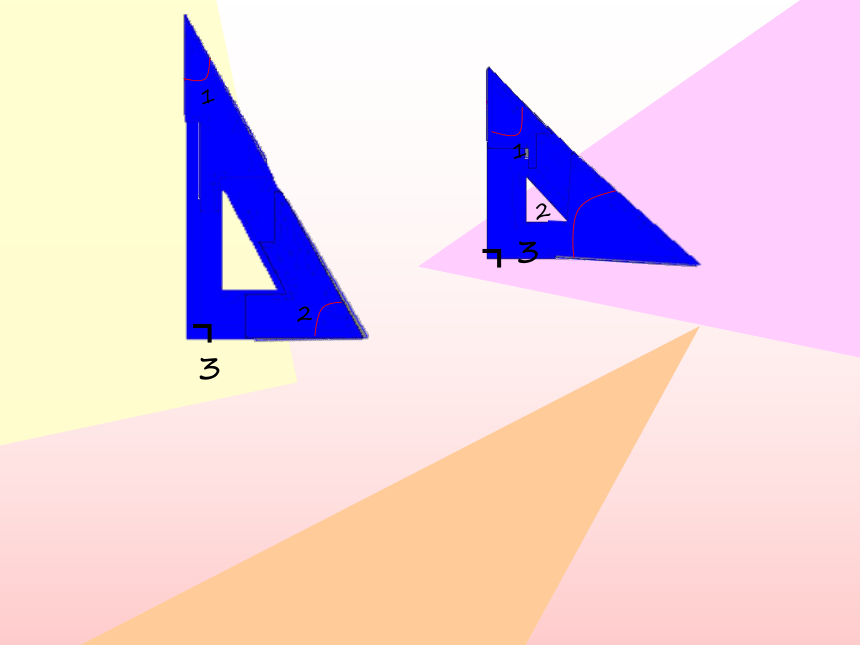
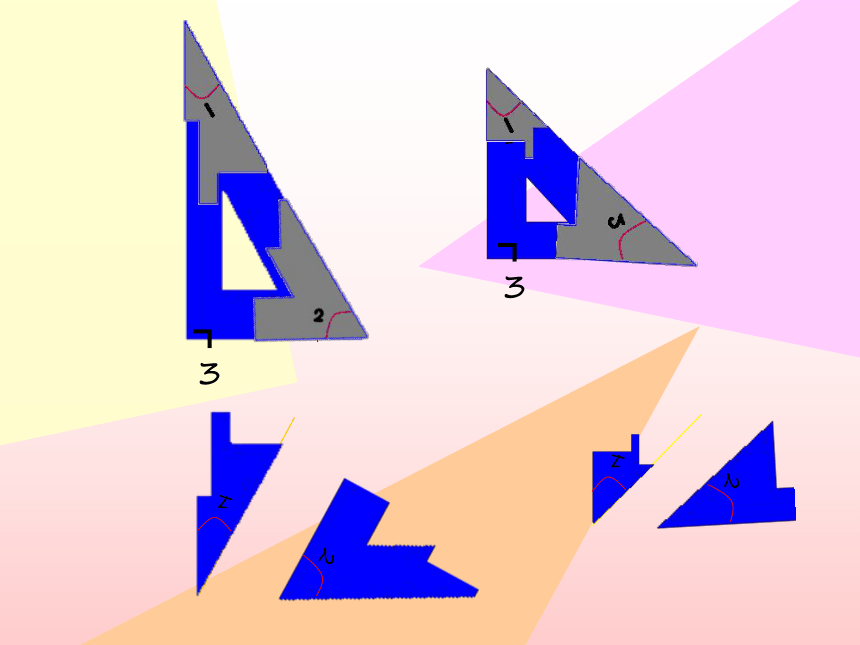
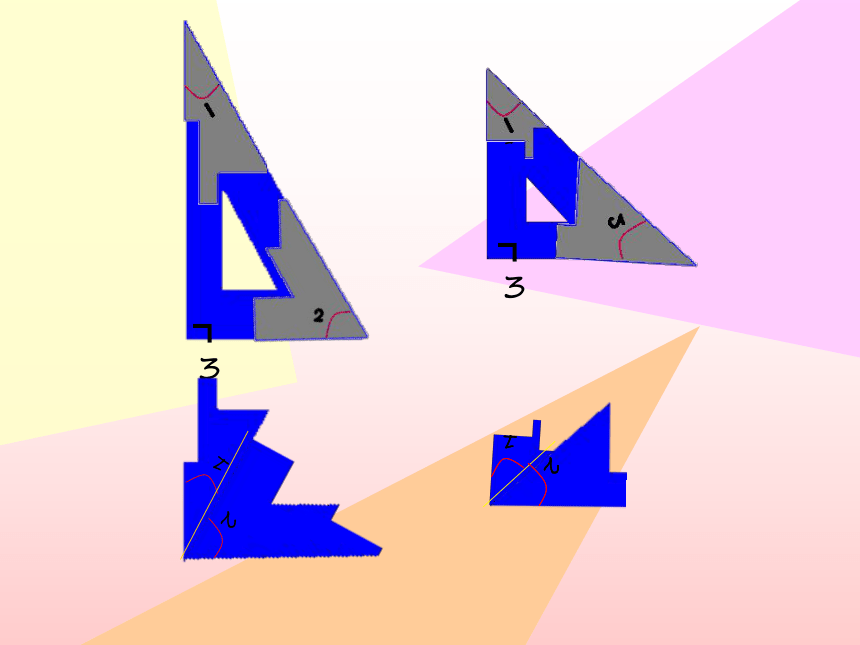
文档简介
(共25张PPT)
人教课标版 七年级 上册
知识回顾:
1、你学过哪些角?
2、填空:
1周角=_____度,1平角=_____度,1直角=____度;
1°=____′=______″ , 1′=______″
_____<锐角<____,_____<钝角<______.
锐角、直角、钝角、平角、周角.
360
180
90
60
3600
60
0°
90°
90°
180°
学习目标:
理解互为余角和互为补角概念
会求一个角的余角和补角
理解余角和补角和性质
利用推理的方法和方程思想解决相关问题
24
1
2
┓3
┓3
1
2
1
2
1
1
2
2
2
2
1
1
┓3
┓3
1
1
2
2
┓3
┓3
2
1
1
2
1
2
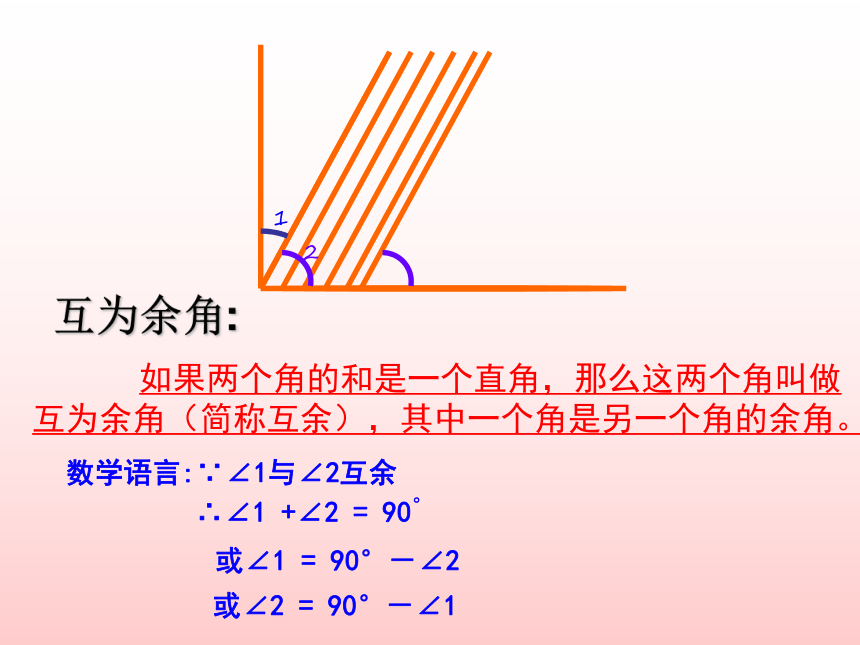
互为余角:
数学语言:∵∠1与∠2互余
如果两个角的和是一个直角,那么这两个角叫做互为余角(简称互余),其中一个角是另一个角的余角。
∴∠1 +∠2 = 90°
或∠1 = 90°-∠2
或∠2 = 90°-∠1
1
2
A
B
C
O
α
β
α
β
α
β
互为补角:
如果两个角的和是一个平角,那么这两个角叫做互为补角(简称互补),其中一个角是另一个角的补角。
数学语言:∵∠1与∠2互补
∴∠1 +∠2 = 180°
或∠1 = 180°-∠2
或∠2 = 180°-∠1
1、若∠1 + ∠2 =180 °,
则______________. ( )
2、若∠1和∠2互补,
则______________. ( )
3、若∠3 + ∠4 =90 °,
则______________. ( )
4、若∠3和∠4互余,
则_________________. ( )
3
4
1
2
∠1和∠2互补
互补定义
∠1 + ∠2 =180 °
互补定义
∠3和∠4互余
互余定义
∠3 + ∠4 =90 °
互余定义
练习
一、填空
1、70°39′的余角是 ,补角是 .
2、如果一个角的补角是150 ° ;那么这个角的余角是 .
3、x °(x<90)的余角是 ,它的补角是 。
109 °21 ′
19 °21 ′
(90-x) °
(180-x) °
总结:锐角∠ 的余角是(90 °—∠ )
∠ 的补角是(180 °—∠ )
60 °
例1:
若一个角的补角等于它的余角的4倍,求这个角的度数。
答:这个角的度数是60 °.
分析:把文字语言翻译成数学语言.补角=___倍余角
4
设这个角是x°,则它的补角是________, 余角是_______.
解:
(180 - x)°
(90-x) °
根据题意得:
(180-x) °= 4 (90-x) °
解得: x =60 °
练习
已知两个角互为补角,它们的差为30 °,求这两个角的度数。
解法1:如果设较小角为x°,
则较大角为(x + 30)°
根据题意,得
x + x + 30 =180
解得 x = 75
∴ x + 30 =105
答:这两个角分别为75°,105°.
解法3:如果设较大角为x°,
则较小角为(x - 30)°
根据题意,得
解得 x = 105
x + x - 30 =180
∴ x - 30 =75
答:这两个角分别为75°,105°.
180 - x =105
x- (180 - x ) =30
180 - x =75
解法2:如果设较小角为x°,
则较大角为为(180 - x )°
解得 x = 75
根据题意,得
(180 - x )-x =30
答:这两个角分别为75°,105°.
解法4:如果设较大角为x°,
则较小角为(180 - x )°
根据题意,得
解得 x = 105
答:这两个角分别为75°,105°.
1、如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?为什么?
答: ∠1 = ∠2.理由如下:
因为∠AOB = 90 °即∠1+ ∠BOD = 90 °
∠COD = 90 ° 即∠2+ ∠BOD = 90 °
所以∠1 = 90 °- ∠BOD
∠2 = 90 °- ∠BOD
则 ∠1 = ∠2
A
O
B
C
D
(结论:同角的余角相等)
1
2
(已知)
(已知)
(余角的定义)
(余角的定义)
(等量减等量其差相等)
2、∠1和∠2互余,∠3和∠4互余,如果∠1=∠3,那么, ∠2和∠4相等吗?为什么?
1
2
3
4
答:相等.
理由如下:
∵ ∠1和∠2互余, ∠3和∠4互余,
∴ ∠2 = 90°- ∠1 ,∠4 = 90°- ∠3
又∵ ∠1 =∠3
∴ ∠2 =∠4
(结论:等角的余角相等)
(已知)
(已知)
(余角的定义)
(等量减等量其差相等)
补角性质:
同角或等角的补角相等.
余角性质:
同角或等角的余角相等.
20
A
B
C
D
E
F
G
如图,E、F是直线DG上两点
∠BEF = ∠BFE
∠AED = ∠CFG = 90 °
找出图中相等的角并说明理由。
∠BED=∠BFG (等角的补角相等)
∠AEB=∠CFB (等角的余角相等)
∠AEG=∠CFD (等角的补角相等)
问题: 要测量两堵围墙围成的角ABC的度数,但人不能进入围墙,如何测量?
A
B
C
D
1、作AB的延长线BD
2、量出∠CBD的度数
3、再求出∠CBD的补角的度数即可.
理由:互补的定义
问题: 要测量两堵围墙围成的角ABC的度数,但人不能进入围墙,如何测量?
D
1、作CB的延长线BD
2、作AB的延长线BE
3、再量出∠EBD的补角的度数即可.
理由:同角的补角相等
E
B
C
A
23
A
O
B
E
D
C
∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90 °
则∠BOC = ,
∠COD = 。
检测
∠DOE
∠AOE
30 °
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等
同角或等角的补角相等
1
2
1
2
1、阅读课本P138~139
2、P139 练习1 、2、3
P141 6、P142 10
人教课标版 七年级 上册
知识回顾:
1、你学过哪些角?
2、填空:
1周角=_____度,1平角=_____度,1直角=____度;
1°=____′=______″ , 1′=______″
_____<锐角<____,_____<钝角<______.
锐角、直角、钝角、平角、周角.
360
180
90
60
3600
60
0°
90°
90°
180°
学习目标:
理解互为余角和互为补角概念
会求一个角的余角和补角
理解余角和补角和性质
利用推理的方法和方程思想解决相关问题
24
1
2
┓3
┓3
1
2
1
2
1
1
2
2
2
2
1
1
┓3
┓3
1
1
2
2
┓3
┓3
2
1
1
2
1
2
互为余角:
数学语言:∵∠1与∠2互余
如果两个角的和是一个直角,那么这两个角叫做互为余角(简称互余),其中一个角是另一个角的余角。
∴∠1 +∠2 = 90°
或∠1 = 90°-∠2
或∠2 = 90°-∠1
1
2
A
B
C
O
α
β
α
β
α
β
互为补角:
如果两个角的和是一个平角,那么这两个角叫做互为补角(简称互补),其中一个角是另一个角的补角。
数学语言:∵∠1与∠2互补
∴∠1 +∠2 = 180°
或∠1 = 180°-∠2
或∠2 = 180°-∠1
1、若∠1 + ∠2 =180 °,
则______________. ( )
2、若∠1和∠2互补,
则______________. ( )
3、若∠3 + ∠4 =90 °,
则______________. ( )
4、若∠3和∠4互余,
则_________________. ( )
3
4
1
2
∠1和∠2互补
互补定义
∠1 + ∠2 =180 °
互补定义
∠3和∠4互余
互余定义
∠3 + ∠4 =90 °
互余定义
练习
一、填空
1、70°39′的余角是 ,补角是 .
2、如果一个角的补角是150 ° ;那么这个角的余角是 .
3、x °(x<90)的余角是 ,它的补角是 。
109 °21 ′
19 °21 ′
(90-x) °
(180-x) °
总结:锐角∠ 的余角是(90 °—∠ )
∠ 的补角是(180 °—∠ )
60 °
例1:
若一个角的补角等于它的余角的4倍,求这个角的度数。
答:这个角的度数是60 °.
分析:把文字语言翻译成数学语言.补角=___倍余角
4
设这个角是x°,则它的补角是________, 余角是_______.
解:
(180 - x)°
(90-x) °
根据题意得:
(180-x) °= 4 (90-x) °
解得: x =60 °
练习
已知两个角互为补角,它们的差为30 °,求这两个角的度数。
解法1:如果设较小角为x°,
则较大角为(x + 30)°
根据题意,得
x + x + 30 =180
解得 x = 75
∴ x + 30 =105
答:这两个角分别为75°,105°.
解法3:如果设较大角为x°,
则较小角为(x - 30)°
根据题意,得
解得 x = 105
x + x - 30 =180
∴ x - 30 =75
答:这两个角分别为75°,105°.
180 - x =105
x- (180 - x ) =30
180 - x =75
解法2:如果设较小角为x°,
则较大角为为(180 - x )°
解得 x = 75
根据题意,得
(180 - x )-x =30
答:这两个角分别为75°,105°.
解法4:如果设较大角为x°,
则较小角为(180 - x )°
根据题意,得
解得 x = 105
答:这两个角分别为75°,105°.
1、如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?为什么?
答: ∠1 = ∠2.理由如下:
因为∠AOB = 90 °即∠1+ ∠BOD = 90 °
∠COD = 90 ° 即∠2+ ∠BOD = 90 °
所以∠1 = 90 °- ∠BOD
∠2 = 90 °- ∠BOD
则 ∠1 = ∠2
A
O
B
C
D
(结论:同角的余角相等)
1
2
(已知)
(已知)
(余角的定义)
(余角的定义)
(等量减等量其差相等)
2、∠1和∠2互余,∠3和∠4互余,如果∠1=∠3,那么, ∠2和∠4相等吗?为什么?
1
2
3
4
答:相等.
理由如下:
∵ ∠1和∠2互余, ∠3和∠4互余,
∴ ∠2 = 90°- ∠1 ,∠4 = 90°- ∠3
又∵ ∠1 =∠3
∴ ∠2 =∠4
(结论:等角的余角相等)
(已知)
(已知)
(余角的定义)
(等量减等量其差相等)
补角性质:
同角或等角的补角相等.
余角性质:
同角或等角的余角相等.
20
A
B
C
D
E
F
G
如图,E、F是直线DG上两点
∠BEF = ∠BFE
∠AED = ∠CFG = 90 °
找出图中相等的角并说明理由。
∠BED=∠BFG (等角的补角相等)
∠AEB=∠CFB (等角的余角相等)
∠AEG=∠CFD (等角的补角相等)
问题: 要测量两堵围墙围成的角ABC的度数,但人不能进入围墙,如何测量?
A
B
C
D
1、作AB的延长线BD
2、量出∠CBD的度数
3、再求出∠CBD的补角的度数即可.
理由:互补的定义
问题: 要测量两堵围墙围成的角ABC的度数,但人不能进入围墙,如何测量?
D
1、作CB的延长线BD
2、作AB的延长线BE
3、再量出∠EBD的补角的度数即可.
理由:同角的补角相等
E
B
C
A
23
A
O
B
E
D
C
∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90 °
则∠BOC = ,
∠COD = 。
检测
∠DOE
∠AOE
30 °
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等
同角或等角的补角相等
1
2
1
2
1、阅读课本P138~139
2、P139 练习1 、2、3
P141 6、P142 10
